[NOIP2004 提高组] 虫食算

题目描述

所谓虫食算，就是原先的算式中有一部分被虫子啃掉了，需要我们根据剩下的数字来判定被啃掉的数字。来看一个简单的例子：

\begin{aligned} \verb!43#9865#045! \\ +\qquad \verb!8468#6633! \\[-1em]\underline{\kern{8em}} \\ \verb!44445509678! \\ \end{aligned}43#9865#045+8468#6633​44445509678​

其中 # 号代表被虫子啃掉的数字。根据算式，我们很容易判断：第一行的两个数字分别是 55 和 33，第二行的数字是 55。

现在，我们对问题做两个限制：

首先，我们只考虑加法的虫食算。这里的加法是 nn 进制加法，算式中三个数都有 nn 位，允许有前导的 00。

其次，虫子把所有的数都啃光了，我们只知道哪些数字是相同的，我们将相同的数字用相同的字母表示，不同的数字用不同的字母表示。如果这个算式是 nn 进制的，我们就取英文字母表的前 nn 个大写字母来表示这个算式中的 00 到 n - 1n−1 这 nn 个不同的数字：但是这 nn 个字母并不一定顺序地代表 00 到 n-1n−1。输入数据保证 nn 个字母分别至少出现一次。

\begin{aligned} \verb!BADC! \\ +\quad \verb!CBDA! \\[-1em]\underline{\kern{4em}} \\ \verb!DCCC! \\ \end{aligned}BADC+CBDA​DCCC​

上面的算式是一个4进制的算式。很显然，我们只要让 \verb!ABCD!ABCD 分别代表 01230123，便可以让这个式子成立了。你的任务是，对于给定的 nn 进制加法算式，求出 nn 个不同的字母分别代表的数字，使得该加法算式成立。输入数据保证有且仅有一组解。

输入格式

输入的第一行是一个整数 nn，代表进制数。

第二到第四行，每行有一个由大写字母组成的字符串，分别代表两个加数以及和。这 33 个字符串左右两端都没有空格，从左到右依次代表从高位到低位，并且恰好有 nn 位。

输出格式

输出一行 nn 个用空格隔开的整数，分别代表 A,B, \dotsA,B,… 代表的数字。

输入输出样例

输入 #1复制

5
ABCED
BDACE
EBBAA

输出 #1复制

1 0 3 4 2

说明/提示

数据规模与约定

• 对于 30\%30% 的数据，保证 n \le 10n≤10；
• 对于 50\%50% 的数据，保证 n \le 15n≤15；
• 对于 100\%100% 的数据，保证 1 \leq n \leq 261≤n≤26。

 

以个位为第一列，di表示第i列的进位情况，对于第i列，如果竖式是

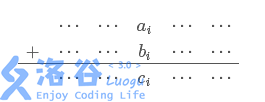
那么显然有

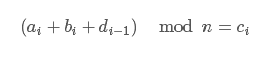
去掉模运算得到

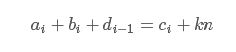
由于这是竖式加法，那么_显然k就是di_。

那就有

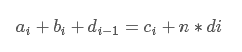
将常数项移到右边去

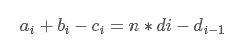
至此，方程列完了。

我们枚举di，进行求解。

显然 

 都是0，所以，我们只需要枚举 

 次，高斯消元的时间复杂度是 

 ，所以总的时间复杂度是 

 ，当然，这显然不够快，考虑优化。

我们发现，我们改变的只有常数项，所以，我们只做一次高斯消元。通过这次高斯消元，我们显然可以求出未知数的系数，那对于_常数项_呢？

##优化从这里开始

设第i个方程的_化简后_的常数项为 

 ，

设高斯消元之后得到的未知数的系数为**_K_**

那么，高斯消元后的矩阵就是这个样子的

我们再用一个数组 

 来保存第i个方程的化简后的常数项和 

 的关系

即 

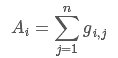
那么显然，初始时， 

那高斯消元后，也就是这个样子

每次枚举出d数组的取值后，我们就可以用 

 的时间算出常数项 

 ，总的时间复杂度变为 

 ，但由于很多取值不用 

 的时间即可判定为不可行_(看我的check()函数)_，所以时间时间会比较短。

##你看懂了吗？（我猜你没看懂）

看看我举的例子：

我们来分析一下样例：

5 ABCED BDACE EBBAA 那么，我们可以列出矩阵

高斯消元后矩阵变为

枚举 

 ，根据增广矩阵的右边算出常数项即可。

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define MAXN 26
int n,equ,var,d[MAXN+10],x[MAXN+10];
typedef int matrix[MAXN+10][MAXN+10];
matrix a,g;
bool vis[MAXN+10];
char s[3][MAXN+10];
void Read(int &x){
    char c;
    while(c=getchar(),c!=EOF)
        if(c>='0'&&c<='9'){
            x=c-'0';
            while(c=getchar(),c>='0')
                x=x*10+c-'0';
            ungetc(c,stdin);
            return;
        }
}
void read(){
    Read(n);
    scanf("%s%s%s",s[0],s[1],s[2]);
    int i,j;
    for(i=0;i<n;i++){
        for(j=0;j<2;j++)
            a[n-i][s[j][i]-'A'+1]++;
        a[n-i][s[2][i]-'A'+1]--;
    }
    for(i=1;i<=n;i++)
        g[i][i]=n,g[i][i-1]=-1;
    g[1][0]=0;
    equ=var=n;
}
int gcd(int a,int b){
    int t;
    while(b){
        t=a%b;
        a=b;
        b=t;
    }
    return a;
}
void gauss_jordan(){
    int i,j,row,col,mxr,lcm;
    for(row=col=1;row<=equ&&col<=var;row++,col++){
        mxr=row;
        for(i=row+1;i<=equ;i++)
            if(abs(a[i][col])>abs(a[mxr][col]))
                mxr=i;
        if(mxr!=row)
            swap(a[row],a[mxr]),swap(g[row],g[mxr]);
        if(!a[row][col]){
            row--;
            continue;
        }
        for(i=1;i<=equ;i++)
            if(i!=row&&a[i][col]){
                lcm=a[i][col]/gcd(a[i][col],a[row][col])*a[row][col];
                int t1=lcm/a[i][col],t2=lcm/a[row][col];
                for(j=1;j<=var;j++){
                    g[i][j]=t1*g[i][j]-t2*g[row][j];
                    a[i][j]=t1*a[i][j]-t2*a[row][j];
                }
            }
    }
}
bool check(){
    int i,j;
    memset(vis,0,sizeof vis);
    for(i=1;i<=n;i++){
        x[i]=0;
        for(j=1;j<=n;j++)
            x[i]+=g[i][j]*d[j];
        if(x[i]%a[i][i]||x[i]/a[i][i]<0||x[i]/a[i][i]>=n||vis[x[i]/a[i][i]])
            return 0;
        x[i]/=a[i][i];
        vis[x[i]]=1;
    }
    return 1;
}
void print(){
    for(int i=1;i<n;i++)
        printf("%d ",x[i]);
    printf("%d\n",x[n]);
}
void dfs(int i){
    if(i==n){
        if(check()){
            print();
            exit(0);
        }
        return;
    }
    d[i]=1;
    dfs(i+1);
    d[i]=0;
    dfs(i+1);
}
int main()
{
    read();
    gauss_jordan();
    dfs(1);
}