1. 树的定义:树( Tree )是n( n≥0 )个结点的有限集。当n=0时称为空树。在任意一颗非空树中:
1>. 有且仅有一个特定的称为根(root)的结点。
2>. 当n>1时,其余结点可分为m( m>0 )个互不相交的有限集T1、T2、……、Tm,其中每一个集合本身又是一颗树,并且称为根的子树( SubTree )。例如:

2. 树节点的分类:结点拥有的子树数量称为结点的度。度为0的结点称为叶节点或终端结点;度不为0的结点称为非终端结点或分支结点。除根节点外,分支结点也称为内部节点。树的度是树内各结点的度的最大值。
3. 树节点之间的关系:结点的子树的根称为该结点的孩子,相应地,该结点称为孩子的双亲。同一个双亲的孩子之间互称兄弟。结点的祖先是从根到该结点所经分支上的所有结点。以某结点为根的子树中任一结点都称为该结点的子孙。
4. 树的层次:结点的层次(Level)从根结点开始定义起,根为第一层,根的孩子为第二层。若某结点在第i层,则其子树的根就在i+1层。其双亲在同一层的结点互为堂兄弟。树中结点的最大层次称为树的深度(Depth)或高度。如:
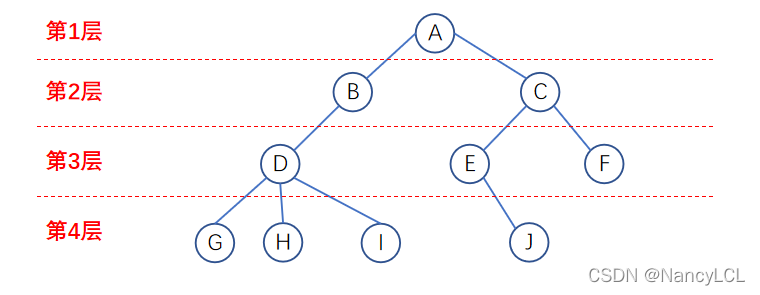








 本文介绍了树形结构的基本概念,包括树的定义、节点分类、节点间的关系以及树的层次。树是由一个根节点和多个子树组成,其中根节点度为1,其余节点分为多个互不相交的子树。节点根据度数可分为叶节点和分支节点,而节点间的关系包括孩子、双亲、兄弟和子孙等。此外,节点的层次从根结点开始,最大层次即为树的深度。
本文介绍了树形结构的基本概念,包括树的定义、节点分类、节点间的关系以及树的层次。树是由一个根节点和多个子树组成,其中根节点度为1,其余节点分为多个互不相交的子树。节点根据度数可分为叶节点和分支节点,而节点间的关系包括孩子、双亲、兄弟和子孙等。此外,节点的层次从根结点开始,最大层次即为树的深度。
















 389
389

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








