DAG(有向无环图)中是否存在环

静下听风声

已于 2023-11-29 18:02:49 修改

阅读量602

点赞数 1

文章标签：深度优先算法图搜索

于 2023-11-29 17:51:13 首次发布

原文链接：https://www.geeksforgeeks.org/detect-cycle-in-a-graph/

版权

给出一个有向图的根节点，判断这个图中是否包含环

例如：

输入：N = 4, E = 6

输出：Yes

说明：由上图可清楚看出环形路径：0 -> 2 -> 0

再如：

输入：N = 4, E = 4

输出：No

说明：上图中不存在环

1.DFS检查有向无环图中环的存在

这个方法思路基于如下：

利用深度优先遍历判断有向图中存在环。基本思想是只有当图中存在指向前置节点的边（暂且称为回向边）时才可能存在环。

为了检测回向边的存在，我们需要标记已经访问过的节点和递归栈（即目前我们的访问路径）中已保存的结点。在递归过程中如果到达的节点已经在递归栈中，说明当前图中存在环。

注意：如果有向图是不连通的，需要获取整个图的森林并分别在各个子图中检查回向边的存在

上述思路的实现步骤：

创建一个递归的dfs函数，包含如下参数：当前节点，已遍历节点的数组和递归栈
标记当前节点为visited并且将其加入到递归栈中
遍历所有节点，对于每个未遍历过的节点调用递归函数（这一步是考虑当前图是一个森林，我们检查每一个子图）：
- 在每个递归调用，找出当前节点的所有未访问过的相邻节点：
  - 如果一个相邻节点已经存在于递归栈中则说明有环，返回true
  - 否则对每个相邻节点调用递归函数
- 当递归调用返回时，清除递归栈中的当前节点，用以代表当前节点不再是已访问路径的一部分
只要任何一个递归调用返回true，停止之后的所有函数调用，并返回true作为结果

示例：

存在如下图：

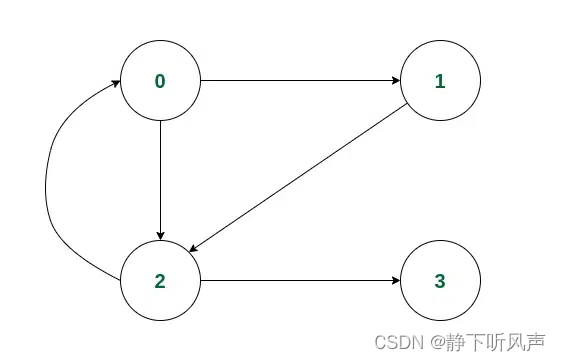
当我们从节点0开始遍历查找：

首先，0会被加入到visited[]和recStack[]数组中作为当前路径的一个节点
现在0的两个相邻节点是1 和 2，假设遍历到节点1 ，那么节点1将会加入到visited[]和recStack[]

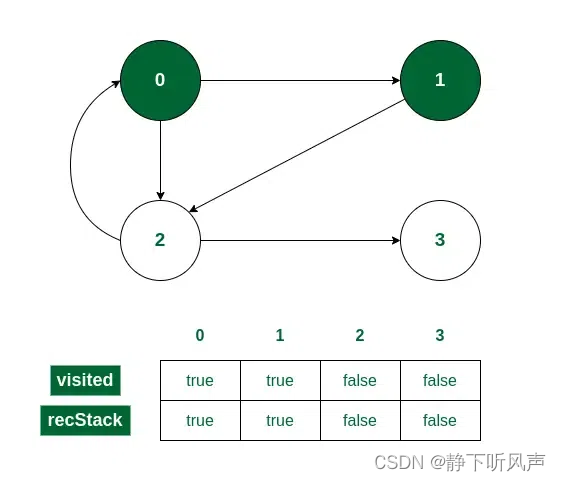
节点1的相邻节点只有一个，递归调用节点2，并将其加入visited[]和recStack[]

Vertex 2 is visited
节点2有两个相邻节点
- 节点0已经访问过并且已经存在于recStack[]，因此如果先检查的是节点0，我们将得到结果是图中存在环
- 另一方面，若先检查的是节点3，那么节点3将会在visited[]和recStack[]数组中
  
  Vertex 3 is visited
当节点3的递归调用返回时，它将从recStack[]中清除，因为节点3现在不是当前路径的一部分

Vertex 3 is unmarked from recStack[]
现在只剩下一个相邻节点0，它已经存在于recStack[]

因些可以得出结论图中存在环。同样地，如果从0节点的相邻节点2开始查找也会得出相同结论。

以下是代码实现：

// A Java Program to detect cycle in a graph
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;

class Graph {

	private final int V;
	private final List<List<Integer> > adj;

	public Graph(int V)
	{
		this.V = V;
		adj = new ArrayList<>(V);

		for (int i = 0; i < V; i++)
			adj.add(new LinkedList<>());
	}

	// Function to check if cycle exists
	private boolean isCyclicUtil(int i, boolean[] visited,
								boolean[] recStack)
	{

		// Mark the current node as visited and
		// part of recursion stack
		if (recStack[i])
			return true;

		if (visited[i])
			return false;

		visited[i] = true;

		recStack[i] = true;
		List<Integer> children = adj.get(i);

		for (Integer c : children)
			if (isCyclicUtil(c, visited, recStack))
				return true;

		recStack[i] = false;

		return false;
	}

	private void addEdge(int source, int dest)
	{
		adj.get(source).add(dest);
	}

	// Returns true if the graph contains a
	// cycle, else false.
	private boolean isCyclic()
	{
		// Mark all the vertices as not visited and
		// not part of recursion stack
		boolean[] visited = new boolean[V];
		boolean[] recStack = new boolean[V];

		// Call the recursive helper function to
		// detect cycle in different DFS trees
		for (int i = 0; i < V; i++)
			if (isCyclicUtil(i, visited, recStack))
				return true;

		return false;
	}

	// Driver code
	public static void main(String[] args)
	{
		Graph graph = new Graph(4);
		graph.addEdge(0, 1);
		graph.addEdge(0, 2);
		graph.addEdge(1, 2);
		graph.addEdge(2, 0);
		graph.addEdge(2, 3);
		graph.addEdge(3, 3);

		// Function call
		if (graph.isCyclic())
			System.out.println("Graph contains cycle");
		else
			System.out.println("Graph doesn't "
							+ "contain cycle");
	}
}

// This code is contributed by Sagar Shah.

输出：

Graph contains cycle

2.使用拓扑排序检测有向图中的环

这里我们使用Kahn算法进行拓扑排序，如果它成功地从图中删除了所有节点，那么它就是一个没有环的DAG。如果剩余的节点存在入度大于0，则表示图形中至少存在一个环。因此，如果我们不能得到拓扑排序中的所有顶点，那么图中至少有一个环存在。

Java代码实现如下：

// Java Program to implement above approach
// Java Program to detect cycle in a graph
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;

class Graph {
	private int V; // number of vertices
	private ArrayList<ArrayList<Integer>> adj; // adjacency list

	public Graph(int V)
	{
		this.V = V;
		adj = new ArrayList<>(V);

		for (int i = 0; i < V; i++) {
			adj.add(new ArrayList<>());
		}
	}

	public void addEdge(int v, int w) { adj.get(v).add(w); }

	public boolean isCyclic()
	{
		int[] inDegree = new int[V]; // stores in-degree of each vertex
        // queue to store vertices with 0 in-degree
		Queue<Integer> q = new LinkedList<>();
		int visited = 0; // count of visited vertices

		// calculate in-degree of each vertex
		for (int u = 0; u < V; u++) {
			for (int v : adj.get(u)) {
				inDegree[v]++;
			}
		}

		// enqueue vertices with 0 in-degree
		for (int u = 0; u < V; u++) {
			if (inDegree[u] == 0) {
				q.add(u);
			}
		}

		// BFS traversal
		while (!q.isEmpty()) {
			int u = q.poll();
			visited++;

			// reduce in-degree of adjacent vertices
			for (int v : adj.get(u)) {
				inDegree[v]--;
				// if in-degree becomes 0, enqueue the
				// vertex
				if (inDegree[v] == 0) {
					q.add(v);
				}
			}
		}
        // if not all vertices are visited, there is a cycle
		return visited != V; 
	}
}
// Driver code
public class Main {
	public static void main(String[] args)
	{
		Graph g = new Graph(6);
		g.addEdge(0, 1);
		g.addEdge(0, 2);
		g.addEdge(1, 3);
		g.addEdge(4, 1);
		g.addEdge(4, 5);
		g.addEdge(5, 3);

		if (g.isCyclic()) {
			System.out.println("Graph contains cycle.");
		}
		else {
			System.out.println(
				"Graph does not contain cycle.");
		}
	}
}

输出：