目录
最近在学习TDOA定位,根据阅读的文献以及自己的推导计算,整理了三种经典的TDOA算法,并利用matlab做了相应的仿真。
一、算法的模型
假设有M个基站参与对目标位置的定位,且第i个基站的位置为![]()
![]() ,目标位置的坐标为
,目标位置的坐标为![]()
![]() ,并且假定信号在各个基站与目标之间是直线传播的,不考虑非直线传播的影响。
,并且假定信号在各个基站与目标之间是直线传播的,不考虑非直线传播的影响。
第i个基站接收到的信号可以表示为
![]() (1)
(1)
其中,s(k)为目标的发射信号,![]()
![]() 为第i个基站的信号时延,
为第i个基站的信号时延,![]()
![]() 为加性高斯白噪声序列,将作S1为参考基站,第i个基站和第一个基站的TDOA测量值为
为加性高斯白噪声序列,将作S1为参考基站,第i个基站和第一个基站的TDOA测量值为
![]()
![]()
![]() (2)
(2)
设TDOA的测量值矢量为![]()
![]()
![]() ,测量误差的协方差矩阵为Q。
,测量误差的协方差矩阵为Q。
将目标与第i个基站的距离表示为
![]() (3)
(3)
等式两边平方可得
![]() (4)
(4)
![]() (5)
(5)
又信号的传播速度为c,于是有
![]() (6)
(6)
通过将(6)这一组非线性方程用适当的方法求解,即可得到对目标位置的估计。
二、Fang算法
Fang算法线性化双曲线方程,通过已知条件得到一元二次方程,计算得到移动台估计位置,有且只能利用三个基站的定位信息,即M=3。
由(6)可知
![]()
![]() (7)
(7)
将式(3)和式(7)联立可得
![]()
![]() (8)
(8)
令i = 1代入(4)并与(8)联立得
![]() (9)
(9)
若把r1,x,y看做未知数,式(9)即变为了线性方程组。
为了简化计算,三个基站坐标分别设为(0,0),(x2,0),![]() (x3,y3),式(9)可以简化如下
(x3,y3),式(9)可以简化如下
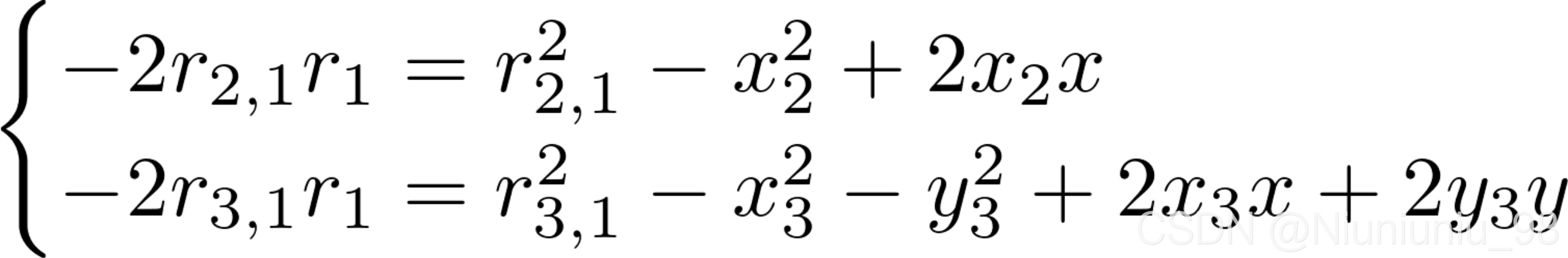 (10)
(10)
两式相减可得
![]()
![]()
![]() (11)
(11)
其中,![]()
![]()

将式(11)代入式(10)可得关于x坐标一元二次方程
![]()
![]()
![]() (12)
(12)
其中,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
通过求解式(12)的一元二次方程就可以得到关于x的两个解,利用先验信息排除掉一个解后,将x代入式(11)得到目标位置的y坐标。
三、Chan算法
Chan算法的推导是基于测量误差为零均值的高斯随机变量。当基站个数大于3个时,非线性方程组个数要少于未知变量的个数,可以利用加权最小二乘法得到初始解,再利用得到的初始解和约束变量进行第二次加权最小二乘法估计,最后得到改进的位置估计。
当M = 3时,可以利用非线性方程直接求解。故主要讨论M > 3的情况。令![]()
![]()
![]() ,
,![]()
![]() 表示不考虑噪声时候的真实值,并且假设x,y,r1线性无关,式(9)可以转变为如下形式
表示不考虑噪声时候的真实值,并且假设x,y,r1线性无关,式(9)可以转变为如下形式
![]()
![]()
![]()
![]() (13)
(13)
其中,
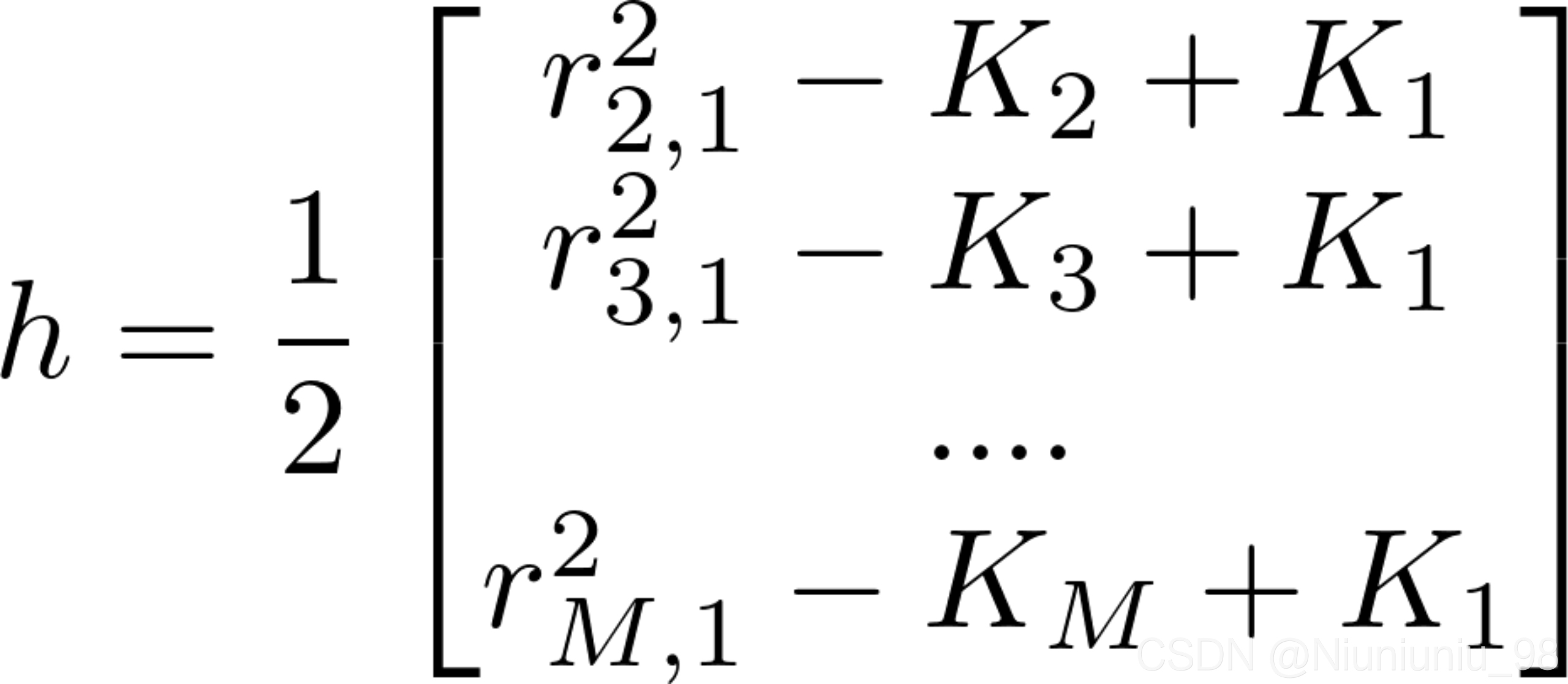 ,
,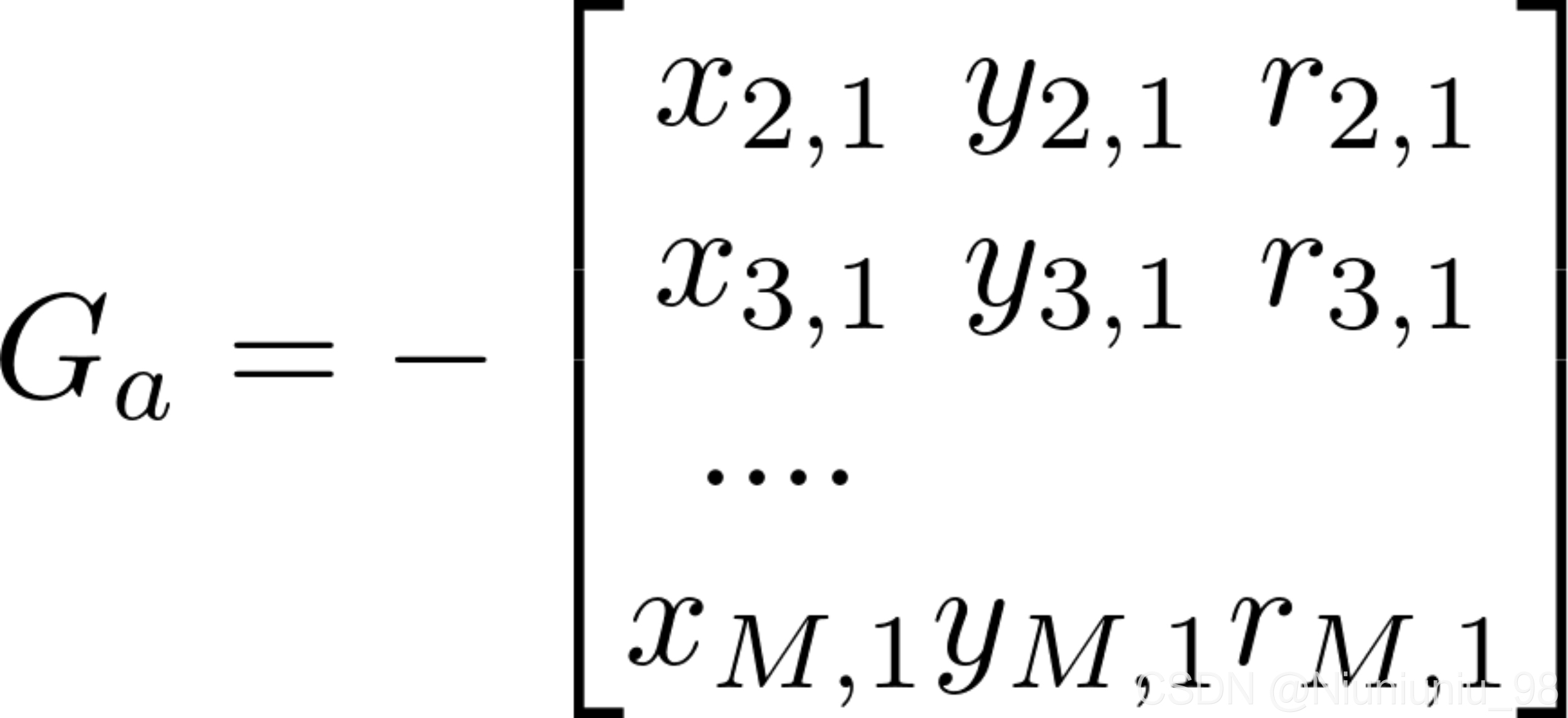
![]()
由于![]()
![]() ,且
,且![]()
![]() ,代入式(13),且忽略二阶误差项,可以得到
,代入式(13),且忽略二阶误差项,可以得到
![]()
![]() (14 )
(14 )
![]()
![]()
![]() (15)
(15)
其中,噪声矢量n服从正态分布,均值为0,协方差矩阵为Q。那么![]() 也服从正态分布,其协方差矩阵为
也服从正态分布,其协方差矩阵为
![]()
![]()
![]() (16)
(16)
关于待求未知量的非线性方程组,我们可以先假定,r1,x,y是不相关的,利用加权最小二乘法求得非线性方程组的解,再考虑未知量的相关关系如i = 1时的式(4),再利用一次加权最小二乘法进行求解,即可获得关于目标的最终估计值。
第一步最小二乘加权:
![]()
![]()
![]() (17)
(17)
![]()
![]()
![]() (18)
(18)
由于目标到基站的实际距离是未知的,因此B是未知的,那么![]() 也是未知的。可以做如下处理。
也是未知的。可以做如下处理。
当目标为远场时,目标到各个基站的距离近似相等,设为![]()
![]() ,从而
,从而![]()
![]() ,因此
,因此![]()
![]() ,而对
,而对![]() 的缩放不会影响定位结果,可以得到一个近似的定位结果
的缩放不会影响定位结果,可以得到一个近似的定位结果
![]()
![]() (19)
(19)
当目标为近场的时候,可以利用(19)求得一个初始估计,利用得到的初始估计求得目标到各个基站的距离,得到B,求解出![]() ,代入(18),即可得到对目标位置的第一步加权最小二乘估计值。
,代入(18),即可得到对目标位置的第一步加权最小二乘估计值。
考虑到噪声,令 ![]()
![]() ,
,![]()
![]()
![]() ,又
,又![]()
![]() ,由式(14)可得
,由式(14)可得
![]()
![]()
![]() (20)
(20)
令![]()
![]()
![]() ,结合式(14)和式(20)可得
,结合式(14)和式(20)可得
![]()
![]()
![]() (21)
(21)
![]()
![]() (22)
(22)
第二步最小加权二乘:
实际上r1,x,y是受到线性制约的,并不是不相关的,将z表示为如下形式
![]()
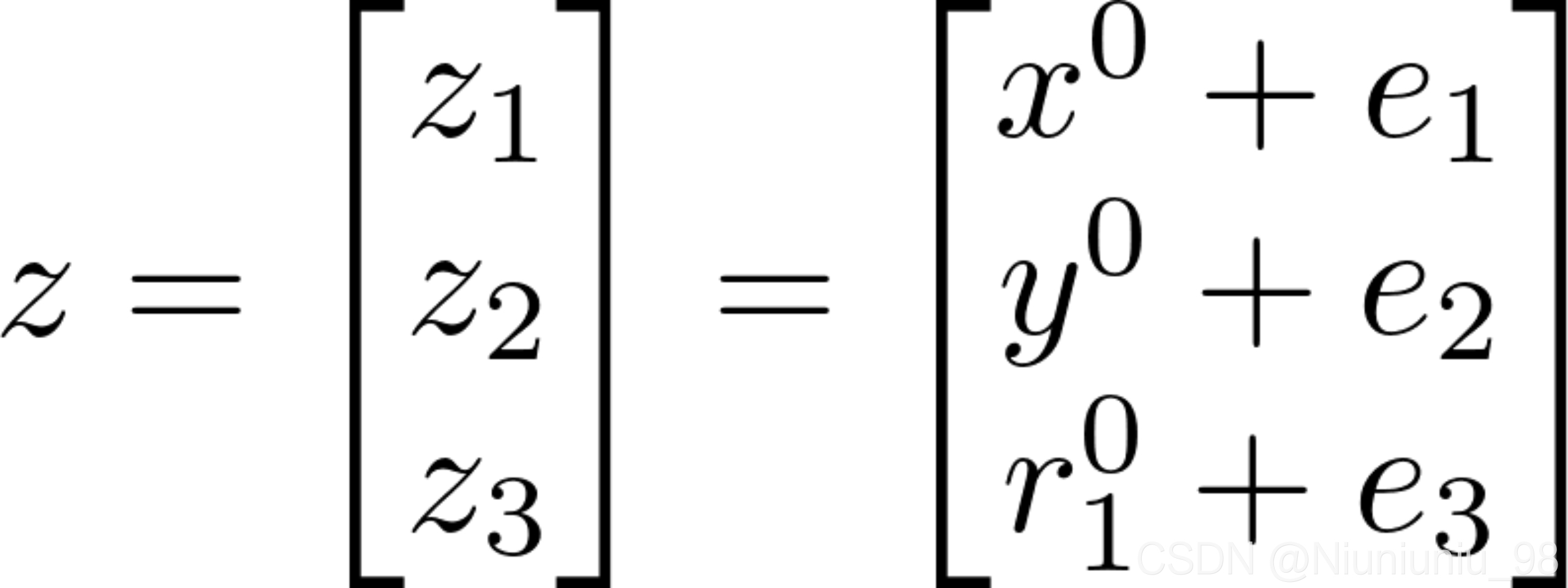 (23)
(23)
其中e1,e2,e3分别为z的估计误差,对式(23)前两个元素减去x1,y1,并将三个元素平方可得到
![]()
![]()
![]() (24)
(24)
其中,
![]()
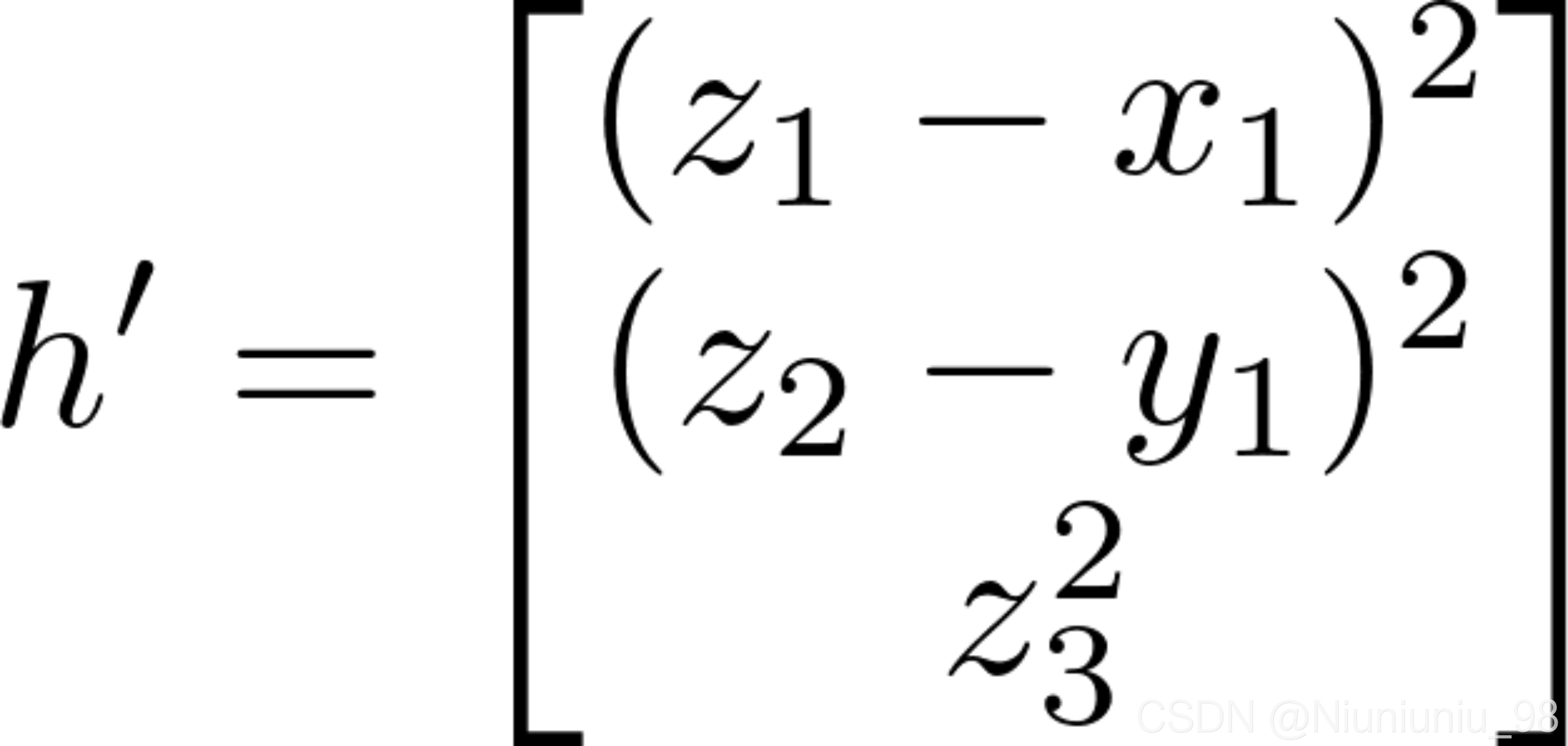 ,
,![]()
 ,
, 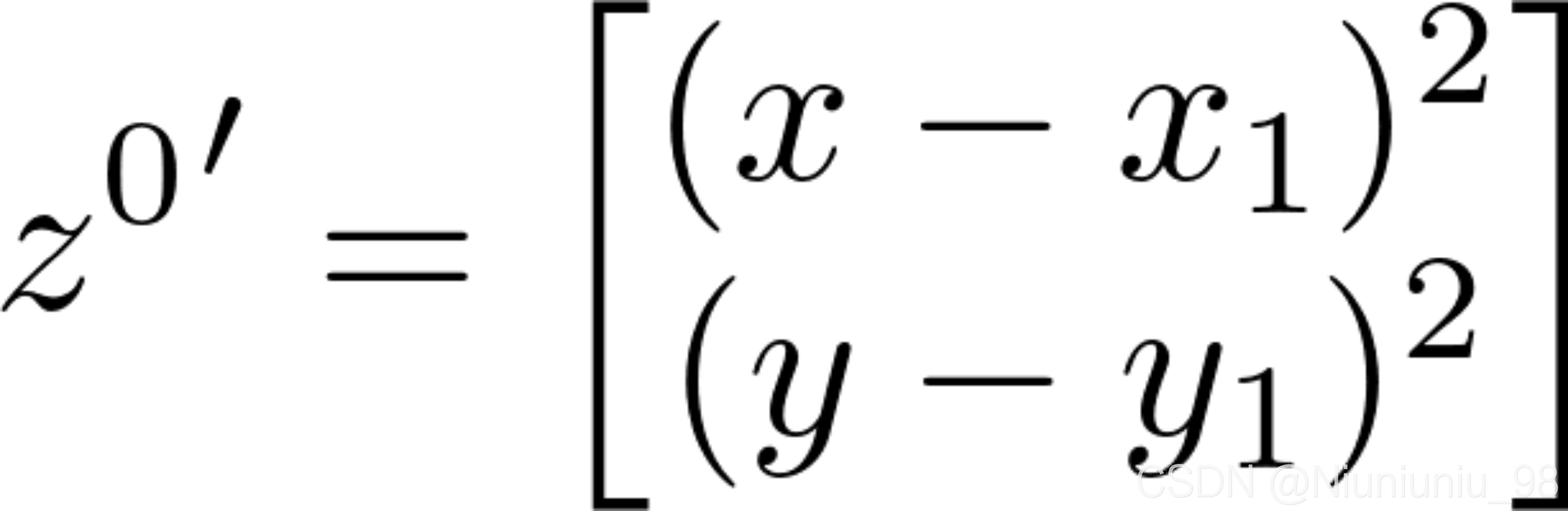
![]()
将式(23)中的各分量代入式(24),并且忽略二阶误差项,求得下面三个等式
![]()
![]()
![]()
![]()
![]()
![]()
![]()
表示成矩阵形式
![]()
![]() (25)
(25)
其中,![]()
![]() ,
,![]() 。
。
误差矢量![]() ‘的协方差矩阵
‘的协方差矩阵![]() ‘可以表示写成如下形式
‘可以表示写成如下形式
![]() (26)
(26)
因此,可以得到z'的加权最小二乘估计,表示如下
![]()
![]()
![]() (27)
(27)
![]() ‘的计算中包含了目标位置的真实坐标,因此是未知的,我们可以利用第一步加权最小二乘法获得的坐标位置的估计来计算矩阵B’,同时用
‘的计算中包含了目标位置的真实坐标,因此是未知的,我们可以利用第一步加权最小二乘法获得的坐标位置的估计来计算矩阵B’,同时用![]()
![]() 代替
代替![]()
![]() ,以此求得
,以此求得![]() ‘,从而求出z'。目标坐标的矢量位置如下,根据先验信息舍去其中一解。
‘,从而求出z'。目标坐标的矢量位置如下,根据先验信息舍去其中一解。
![]()
![]()
该算法能充分利用各个基站的TDOA测量值信息,有效减少个别基站测量误差较大对定位产生的负面影响。但是忽略掉了二阶误差项,对于实际环境中误差较大的测量值,比如在有非视距传播的情况下,算法性能会显著下降。
四、泰勒级数法
Taylor算法将方程组的各式在初始目标位置处进行泰勒级数一阶展开,采用迭代的方式求解。
将和代入(6)可以得到
![]()
![]()
![]() (29)
(29)
首先要对目标位置给定一个初始估计![]()
![]()
![]() ,可以由加权最小二乘法得到。对(29)在初始估计位置处进行一阶泰勒级数展开,可以得到
,可以由加权最小二乘法得到。对(29)在初始估计位置处进行一阶泰勒级数展开,可以得到
![]()
![]()
![]() (30)
(30)
其中,![]()
![]() 表示残差,
表示残差,![]()
![]()
![]() 表示对目标未知估计的误差矢量。且
表示对目标未知估计的误差矢量。且
![]()
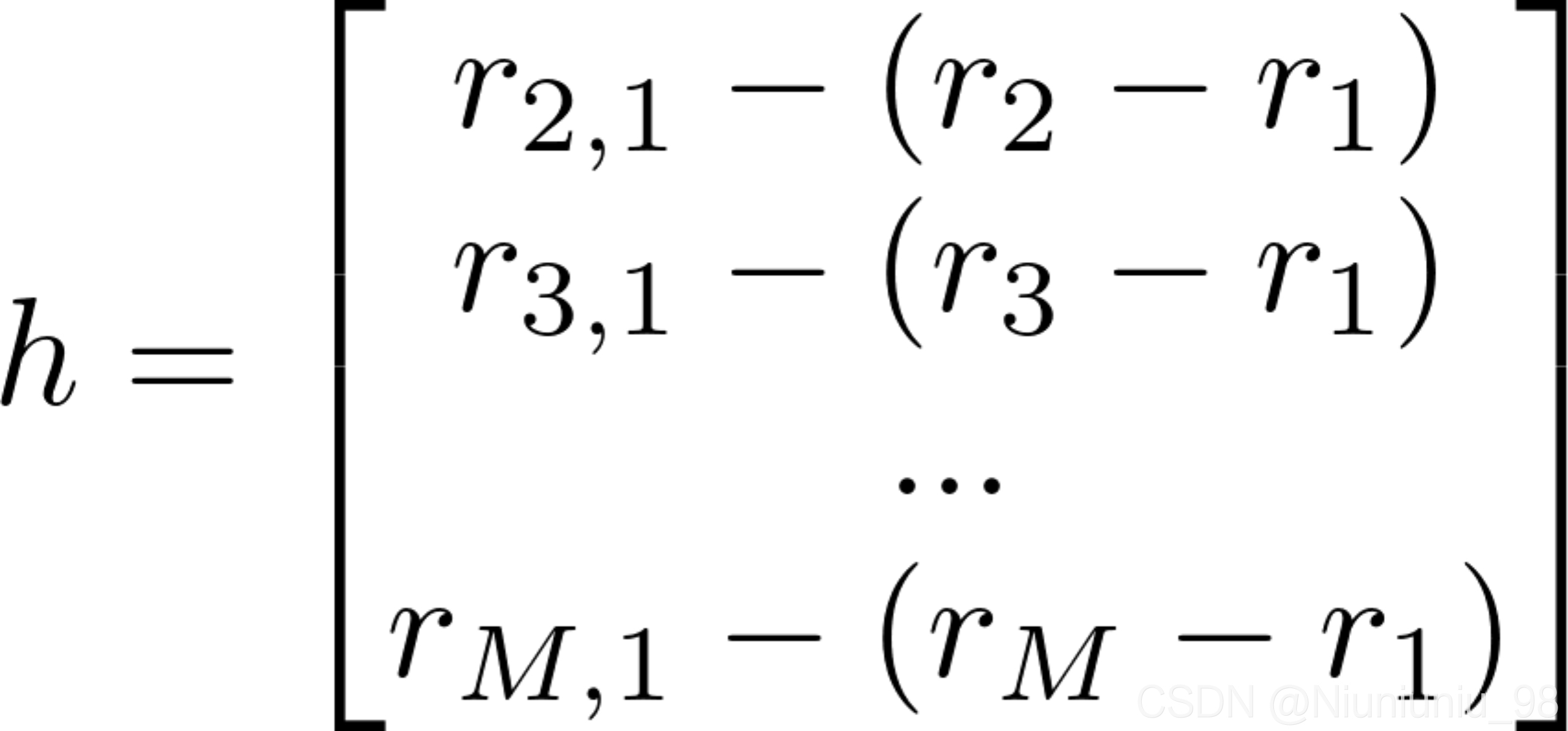 ,
,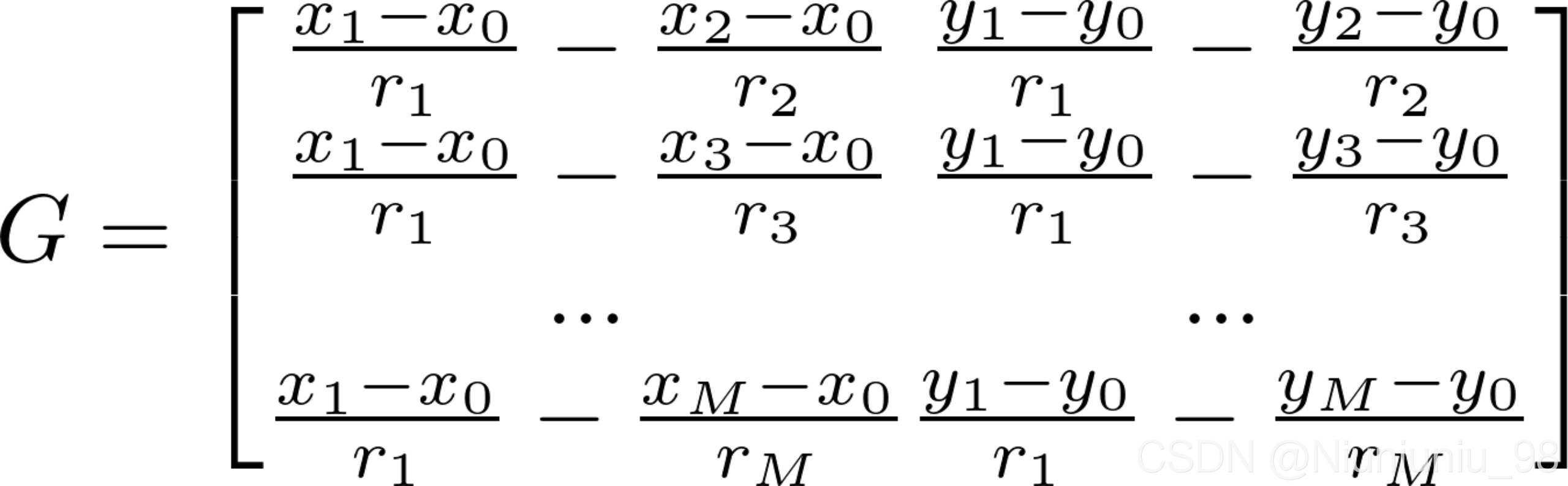
式(30)的加权最小二乘解为
![]()
![]()
![]()
![]() (31)
(31)
在下一步的迭代中,我们将x0,y0重新设置为![]() ,
,![]() ,继续上面的过程,直到
,继续上面的过程,直到![]()
![]()
和
![]() 充分小,满足迭代停止条件,即可得到对目标未知的估计,为
充分小,满足迭代停止条件,即可得到对目标未知的估计,为![]()
![]()
![]()
![]() 。
。
在初始目标位置选取较好的情况下,Taylor法的定位精度很高,并且算法收敛较快。若初始目标位置选取不好,该算法计算量很大,且容易落到局部最小点,收敛性难以保障。








 本文详细介绍了TDOA(到达时间差)定位的三种经典算法:Fang算法、Chan算法和泰勒级数法。Fang算法适用于三个基站的定位,通过线性化双曲线方程求解。Chan算法则在基站数量大于3时,利用加权最小二乘法进行两次迭代求解。泰勒级数法则通过目标位置的迭代逼近提高定位精度。这些算法在不同场景下各有优势,但都受限于非线性方程的求解和噪声影响。
本文详细介绍了TDOA(到达时间差)定位的三种经典算法:Fang算法、Chan算法和泰勒级数法。Fang算法适用于三个基站的定位,通过线性化双曲线方程求解。Chan算法则在基站数量大于3时,利用加权最小二乘法进行两次迭代求解。泰勒级数法则通过目标位置的迭代逼近提高定位精度。这些算法在不同场景下各有优势,但都受限于非线性方程的求解和噪声影响。
















 767
767

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








