常用求素数的方法

* 题外：回文素数一定是奇数位abcba式的证明：

（跟求素数没啥关系，就是刚好看见顺便记下，怕又忘了……）

1. 偶回文数的各个数位可以分解为 n * 100…001(两个1中间若干个0)的形式
   而这个 100…001 是能被11整除的，所以偶数位的回文数一定不是质数……

2. 一个整数如果奇数位的数字和等于偶数位的数字和，则其能被11整除。如果一个回文数的长度为偶数，则显然有这个特征。由此完成证明.

嗯，说正事！

1.通过性质判断 :

• <= sqrt(n)(常用 n/2 代替)

• 六倍原理：(必要条件 ： 如 ‘ 25 ’ 符合条件但不是素数)
  当 n >= 5时，若n是素数，则 n = 6k + 1 or n = 6k-1

  证明：
  6k-3,6k+3显然能被 3 整除；6k-2,6k+2显然能被2整除，6k就不说了，所以显然就剩 6k-1,6k+1俩了，自然就在这个范围内找了（注意包括2,3）……

2.筛法判断：（数量较大，均围绕着“素数的倍数不是素数”进行筛选）

* 普通筛法—埃氏筛法

原理：

要得到自然数n以内的全部素数，必须把不大于根号n的所有素数的倍数剔除，剩下的就是素数。
给出要筛数值的范围n，找出n以内的素数：先用2去筛，即把2留下，把2的倍数剔除掉；再用下一个质数，也就是3筛，把3留下，把3的倍数剔除掉；接下去用下一个质数5筛，把5留下，把5的倍数剔除掉；不断重复下去…

注意：

素数是在删的过程中就能依次得到！而不是所有删除操作结束后才能得到！因为选取的数是依次递增的……

原理图如下，我就是个搬运工……

const int MAX = 9999; 
int b[MAX];
int a[MAX] = {0};
int k = 0;
for(int i = 2;i <= n;i++){  // n 为所求范围 
	if(a[i] == 0){ //未被筛去
	 
		for(int j = 2;i * j <= n;j++){
			    a[i*j] = 1;
		}
		b[k++] = i;  // 记录该素数 
	}
}

算法的时间复杂度为O(nloglogn)，（额，不会证……）感觉还可以，but……在删除的过程中做了很多重复的工作，
比如 15 既是 3 的倍数又是 5 的倍数，会被筛两次。为了减少这种不必要的操作，因此我们将埃氏筛法进行改进，有了欧拉筛法：

* 线性筛法—欧拉函数筛法

改进：让每个合数只被其最小质因数筛一次，让算法复杂度从O(nloglogn)降到了 O(n)

先上代码吧

const int MAX = 9999; 
int b[MAX];
int a[MAX] = {0};
int k = 0;
for(int i = 2;i <= n;i++){  // n 为所求范围 
	if(a[i] == 0)//未被筛去
		b[k++] = i;  // 记录该素数 
		
		for(int j = 0;j < k && i * b[j] <= n;j++){
			     a[i * b[j]] = 1;
			     if(i % b[j] == 0) break; // 当 a[i] != 0 时 
		}
	}

对于欧拉筛法对埃氏筛法的优化，

举个栗子说话 ，比如删 以素数 3为因数的那些合数：

从上面代码有 b[1] = 3, 通过 i * b[j] 来筛去3的倍数：3* 3， 5 * 3 , 7*3……等i为大于等于b[1]的奇数的倍数，而对于i 为偶数的倍数（令m = i * b[1]），通过b[1]根本计算不到，因为在 i % b[0] == 0 这一步判断时便被排除了，m只能被2筛去，这符合欧拉筛法的优化思想，每个数只出现一次，证明在下面……

而对于 i倍数比3本身小的数，如6，没有2 * 3，只能通过 3 * 2 被筛去，这恰是埃氏筛法的薄弱之处了（对于6，既会被2筛一次，又会被3筛一次，即6会多次出现，此后再筛都是 做的重复工作）事实上对于任一合数，欧拉筛法能做到，一个合数一定是被其最小质因数筛去的，且该合数只出现一次，这样便减少了很多不必要的计算。

个人理解证明如下：

对于任意合数m = a * b;(a < b,符合 b[j] * i )

1.a,b均为奇数

若a 可分解，则只能分解为多个奇数相乘，对b同样如此，此时 m = (a₁ * a₂……a_n) * (b₁ * b₂……b_n)，将a_i 与 b_i 进行随机组合得 m = a’ * b’,所有组合在数轴上的分布如下：
（注：由于自由组合个数还是挺多的，懒得全部列出，但道理是一样的）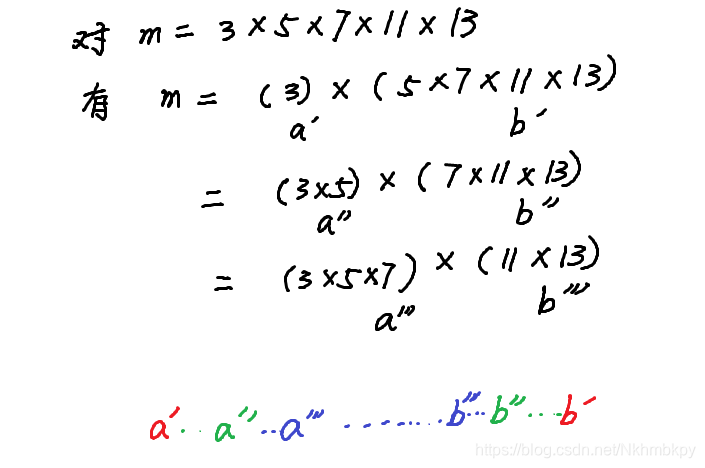
易得，将 a * b 对应为 b[j] * i，可知除了第一种情况外，其他情况都是不成立的，因为b[j]只能为素数，即意味着对于i =（7 * 11 * 13）不存在 b[j] =（3 * 5）,也就不会出现m,其他的情况如此类推

2.其他情况

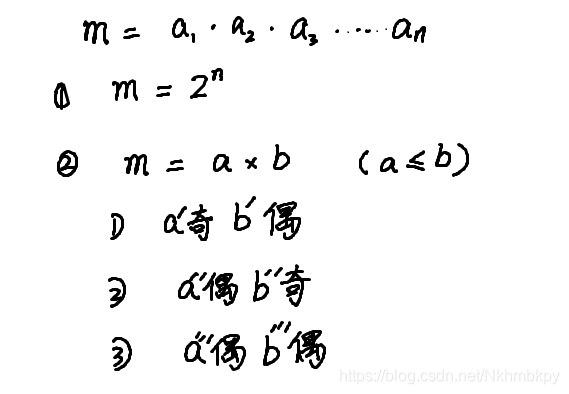
将所有 a_i分成两堆后能得到上面三种情况，
对于 m = 2ⁿ,易得循环中只有 m = i * b[0] 这一种情况能出现，

对于第一种，若a’ 是可分解的，分解方式同第一种，那b[j]中一定只存在那个最小的 a’,使得 a’ * b’ = m,（不然作为一个可分解的合数，是没有资格出现在b[j]中的，下面的理由相同）

对于第二种情况，a”除非是2，否则不存在于b[j]中，因此同样只会有一个 a” * b” = m;

对于第三种情况，依然是除非 a’” 是2，否则不会出现，事实上2）、3）可归为一种，因为 i 的取值只要 >= 2即可

综上我们可以得出结论，对于任意一个合数，a[ i*b[j] ] = 1 的计算都只会出现一次！即优化可行。