AC自动机详解(c++超详细版)-CSDN博客

本文链接：https://blog.csdn.net/OneFlowers/article/details/149350196

AC自动机的原理
AC自动机：Aho-Corasick automation, 该算法在1975年产生于贝尔实验室，是著名的多模式串匹配算法之一。一个常见的例子就是给出 n 个单词，再给出一段包含 m 个字符的文章，让你找出有多少个单词在文章里出现过。
要搞懂AC 自动机，先得有字典树Trie 和 KMP 模式匹配算法的基础知识。KMP 算法是单模式串的字符匹配算法，AC自动机是多模式串的字符匹配算法。
AC 自动机的构造：

构造一棵Trie, 作为AC 自动机的搜索数据结构。
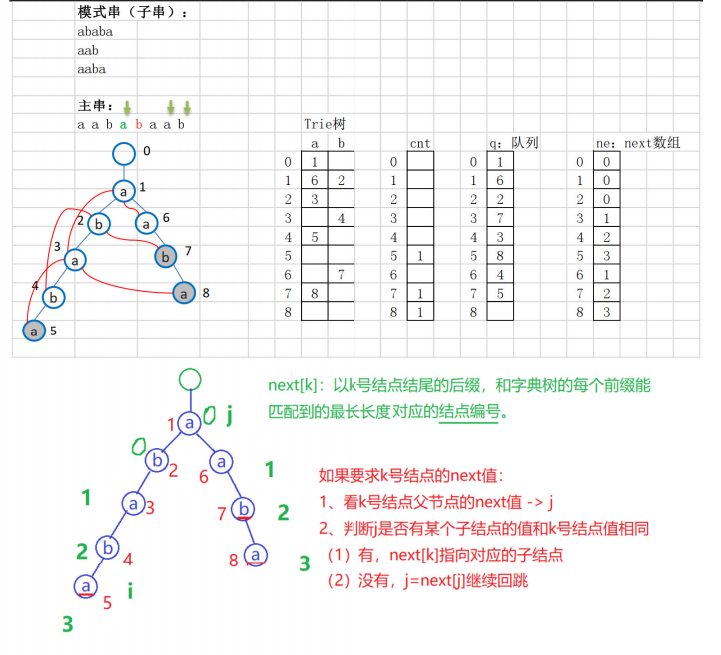
构造next 指针，使当前字符失配时跳转到具有最长公共前后缀的字符继续匹配。如同 KMP算法一样，AC自动机在匹配时如果当前字符匹配失败，那么利用next 指针进行跳转。由此可知如果跳转，跳转后的串的前缀，必为跳转前的模式串的后缀并且跳转的新位置的深度(匹配字符个数)一定小于跳之前的节点。所以我们可以利用 bfs 在 Trie 上面进行 next 指针的求解。
如果要求k 号结点的next 值：
(1)看 k 号结点父节点的next 值 - > j
(2)判断j 是否有某个子结点的值和k 号结点值相同
A、有，next[k] 指向对应的子结点
B、没有，j=next[j] 继续回跳，直到跳到根
扫描主串进行匹配。
AC 自动机相当于：Trie +KMP的组合。
AC 自动机，可以优化为 Trie 图。

例题：
在这里插入图片描述

#include<bits/stdc++.h>
using namespace std;
/*
1.将多个单词创建Trie 字典树
2.求解字典树每个结点的next  值
3.KMP 匹配
*/
const int N=1e4+10,M=1e6+10,L=55;
int T,n;
int ch[N*L][26],idx,cnt[N*L];
int ne[N*L];//每个结点对应的next 值 
int q[N*L]; //队列
char w[L],s[M]; //单词和文章 

//多组数据计算时，每组数据计算要先清空部分变量的值
void init(){
	memset(ch,0,sizeof(ch));
	memset(cnt,0,sizeof(cnt));
	memset(ne,0,sizeof(ne));
	idx=0;
}

//建字典树
void insert(char w[]){
	int t=0;//从根结点开始讨论 
	for(int i=0;w[i]!='\0';i++){
		int x=w[i]-'a';
		if(ch[t][x]==0) ch[t][x]=++idx;
		t=ch[t][x];
	}
	cnt[t]++;	// 以当前结点结束的单词数+1 
}

//求每个结点的next  值 
void get_next(){
	int h=1,t=0;//默认队列为空
	//将根节点下面的第一层结点入队
	//因为这一层的结点的 next 值都是0
	for(int i=0;i<26;i++){
		if(ch[0][i]) q[++t]=ch[0][i];
	}
	//计算每一层结点的next 值
	while(h<=t){
		int f=q[h];//当前这一层的上一层的父元素的编号 
		for(int i=0;i<26;i++){
			if(ch[f][i]){
				int c=ch[f][i];//获取子结点的编号
				int j=ne[f];//获取父元素的next 值
				while(j&&!ch[j][i]) j=ne[j];
				if(ch[j][i]) j=ch[j][i];
				ne[c]=j;
				q[++t]=c;//入队
			}
		}
		h++;//出队
	}
}

int main(){
	cin>>T;
	while(T--){
		init();
		cin>>n;
		for(int i=1;i<=n;i++){
			scanf("%s",w);
			insert(w);
		}
		get_next();
		scanf("%s",s);
		int res=0;
		//kmp匹配 
		//i: 代表遍历s 字符串
		//j: 代表字典树从根结点开始遍历
		for(int i=0,j=0;s[i];i++){
			int x=s[i]-'a';
			while(j&&ch[j][x]==0) j=ne[j];
			if(ch[j][x]!=0) j=ch[j][x];
			int p=j;
			//计数
			while(p!=0){
				res+=cnt[p];
				cnt[p]=0;
				p=ne[p];
			}
		}
		cout<<res<<endl;	
	}
    return 0;
}

例题2：（写法2：参考yyb大神代码）（建议学习这种写法，fail相当于next的概念）

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<queue>
#include<algorithm>
using namespace std;
struct Tree//字典树 
{
     int fail;//失配指针
     int vis[26];//子节点的位置
     int end;//标记有几个单词以这个节点结尾 
}AC[1000000];//Trie树
int cnt=0;//Trie的指针 
inline void Build(string s)
{
        int l=s.length();
        int now=0;//字典树的当前指针 
        for(int i=0;i<l;++i)//构造Trie树
        {
                if(AC[now].vis[s[i]-'a']==0)//Trie树没有这个子节点
                   AC[now].vis[s[i]-'a']=++cnt;//构造出来
                now=AC[now].vis[s[i]-'a'];//向下构造 
        }
        AC[now].end+=1;//标记单词结尾 
}
void Get_fail()//构造fail指针
{
        queue<int> Q;//队列 
        for(int i=0;i<26;++i)//第二层的fail指针提前处理一下
        {
               if(AC[0].vis[i]!=0)
               {
                   AC[AC[0].vis[i]].fail=0;//指向根节点
                   Q.push(AC[0].vis[i]);//压入队列 
               }
        }
        while(!Q.empty())//BFS求fail指针 
        {
              int u=Q.front();
              Q.pop();
              for(int i=0;i<26;++i)//枚举所有子节点
              {
                        if(AC[u].vis[i]!=0)//存在这个子节点
                      {
                                AC[AC[u].vis[i]].fail=AC[AC[u].fail].vis[i];
                                    //子节点的fail指针指向当前节点的
                                  //fail指针所指向的节点的相同子节点 
                                Q.push(AC[u].vis[i]);//压入队列 
                      }
                      else//不存在这个子节点 
                      AC[u].vis[i]=AC[AC[u].fail].vis[i];
                      //当前节点的这个子节点指向当
                      //前节点fail指针的这个子节点 
              }
        }
}
int AC_Query(string s)//AC自动机匹配
{
        int l=s.length();
        int now=0,ans=0;
        for(int i=0;i<l;++i)
        {
                now=AC[now].vis[s[i]-'a'];//向下一层
                for(int t=now;t&&AC[t].end!=-1;t=AC[t].fail)//循环求解
                {
                         ans+=AC[t].end;
                         AC[t].end=-1;
                } 
        }
        return ans;
}
int main()
{
     int n;
     string s;
     cin>>n;
     for(int i=1;i<=n;++i)
     {
             cin>>s;
             Build(s);
     }
     AC[0].fail=0;//结束标志 
     Get_fail();//求出失配指针
     cin>>s;//文本串 
     cout<<AC_Query(s)<<endl;
     return 0;
}