Python-非线性方程（组）求出所有的数值解

 Python的Scipy库中有fsolve等函数用于求解非线性方程（组）的数值解，但需要给定一个初始的猜测值，该值的选取对于方程的求解有时很重要，选取的不好甚至求不出解。但在能给出解的情况下，也只能给出一个解，但非线性方程（组）的解可能不是唯一的，本文介绍几种设置初始猜测值从而求出所有数值解的办法。

一、方法介绍

1. 对于简单的方程组（特别是单个变量的方程），可以采用数形结合的办法，画出函数的图像，观察零点（or交点）的大概位置，然后将初始猜测值分别选取在这几个点的附近，从而找出所有的解。
2. 对于复杂的方程组，可能不太方便可视化解的分布，这时候可以对初始猜测值在一定范围内进行遍历，注意这个范围的选取可能与变量的物理含义有关（例如长度不能小于0）。注意这样遍历初始猜测值求出来的解一般是会重复的，最后再将重复的解去掉即可。

---

二、一个数学建模中的案例

下面以一个题目为例来介绍一下具体的应用，题目来源于Datawhale 数学建模教程

图1 平面型Stewart平台示意图

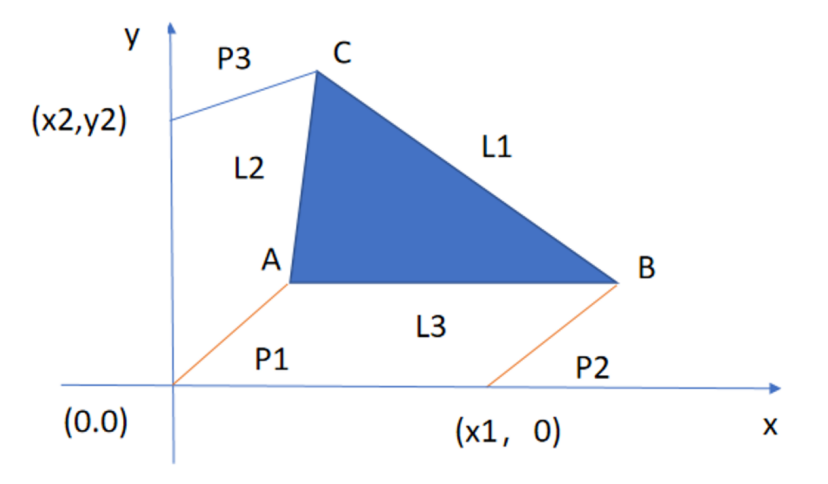
 图1给出的是平台型Stewart平台示意图，它模拟一个操作装置，其中包括一个三角形()平台,平台位于由3个支柱（, 和控制的固定平面中）。图中的三角形表示平面型Stewart平台，它的尺寸由3个长度，，确定。平台的位置由3个支柱的可变长度的3个参数, 和所控制。需要解决的问题是，在给定一组参数, , 的值后，计算出点的坐标和角度的值（是与轴的夹角），请你完成：

1. 数学建模：参数L1​,L2​,L3​,x1​,x2​,y2​是固定常数，在给定一组参数P1​,P2​,P3​的值后，判断能否得到Stewart平台的一个位置，即能否得到A点坐标(x,y)和角度θ的值。如果能，则称它为Stewart平台的一个位姿。但位姿并不一定是唯一的，如何让你的模型能够计算出一组固定参数下的全部位姿。
2. 模型检验：假设有如下参数: x1​=5, (x2​,y2​)=(0,6)，L1​=L2=L3​=3, P1​=P2​=5, P3​=3，请根据你的模型，计算出Stewart平台的全部位姿，即计算出每个Stewart平台中的A点坐标(x,y)和角度θ的值。

---

三、案例求解

这个问题不算太难，有三个待求的未知数(x,y)和θ，而根据每个支柱的长度用两点间的距离公式就可以建立3个方程，具体的可参考Datawhale 数学建模教程。因此接下来需要做的就是求解这个非线性方程组。

首先看一下Datawhale 数学建模教程中给出的Baseline代码，该代码通过fsolve函数数值求解建立的方程组，其中初始猜测值initial_guess则是给定的是[-1.37, 4.80, 0.12]，最后求出来一组解[1.15769945 4.86412705 0.02143414]。

from scipy.optimize import fsolve
from math import sin, cos, pi
# 定义方程组
def equations(vars):
    x, y, theta = vars
    L1, L2, L3 = 3, 3, 3
    p1, p2, p3 = 5, 5, 3
    x1, x2, y2 = 5, 0, 6
    # 根据问题描述定义的方程
    eq1 = (x + L3*cos(theta) - x1)**2 + (y + L3*sin(theta))**2 - p2**2
    eq2 = x**2 + y**2 - p1**2
    eq3 = (x + L2*cos(pi/3 + theta))**2 + (y + L2*sin(pi/3 + theta) - y2)**2 - p3**2
    return [eq1, eq2, eq3]
# 初始猜测值
initial_guess = [-1.37, 4.80, 0.12]
# 使用fsolve求解方程组
result = fsolve(equations, initial_guess)
print(result)
# [1.15769945 4.86412705 0.02143414]

但是就如题干所说，是否存在其他解呢。这里我们对Baseline算法进行了改进，由于方程组较复杂，采用了第一节介绍的遍历的方法，具体代码如下：

from scipy.optimize import fsolve
from math import sin, cos, pi, acos
import numpy as np
import matplotlib.pyplot as plt

L1, L2, L3 = 3, 3, 3
p1, p2, p3 = 5, 5, 3
x1, x2, y2 = 5, 0, 6
# 用余弦定理计算三角形内角beta
beta = acos((L2 ** 2 + L3 ** 2 - L1 ** 2) / (2 * L2 * L3))

# 定义方程组
def equations(vars):
    x, y, theta = vars
    # 根据问题描述定义的方程
    eq1 = (x + L3 * cos(theta) - x1) ** 2 + (y + L3 * sin(theta)) ** 2 - p2 ** 2
    eq2 = x ** 2 + y ** 2 - p1 ** 2
    eq3 = (x + L2 * cos(beta + theta) - x2) ** 2 + (y + L2 * sin(beta + theta) - y2) ** 2 - p3 ** 2
    return [eq1, eq2, eq3]


result_group = []
for angle in np.linspace(0, 2 * pi, 20):
    # 初始猜测值
    x0 = p1 * cos(angle)
    y0 = p1 * sin(angle)
    for theta0 in np.linspace(0, 2 * pi, 20):
        initial_guess = [x0, y0, theta0]
        # 使用 fsolve 求解方程组
        result = fsolve(equations, initial_guess)
        if ((np.isclose(equations(result), [0.0, 0.0, 0.0]) == [True, True, True]).all()) and 0 <= result[-1] < 2 * pi:  #验证是否为真解
            if result_group == []:
                result_group.append(result)
            else:
                repeated_root = False
                for ii in range(len(result_group)):   # 去除重根
                    if ((result - result_group[ii]) < 1e-5).all():
                        repeated_root = True  # 是重根
                        break
                if not repeated_root:
                    result_group.append(result)
print(result_group) # 多解数组
# [array([1.15769945, 4.86412705, 0.02143414]), array([-0.43369482,  4.98115537,  5.01916275])]

可以看出方程的建立与Baseline一样，但是initial_guess并没有采用一个固定的值，而是用2个for循环遍历空间中可能的值。（这里angle和theta0在0~2pi中等间距取了20个点，如果解很多时，应取更多的点以防止漏解）

将得到的解存在result_group中，并去除了重根。结果显示存在两组解[array([1.15769945, 4.86412705, 0.02143414]), array([-0.43369482,  4.98115537,  5.01916275])]。为了进一步的可视化，我们分别画出了这两组解所对应的Stewart平台示意图如下。

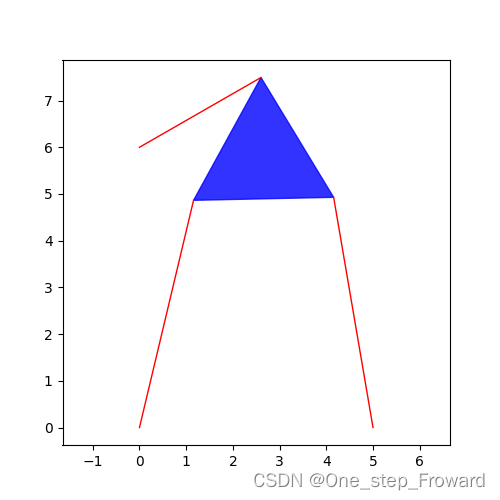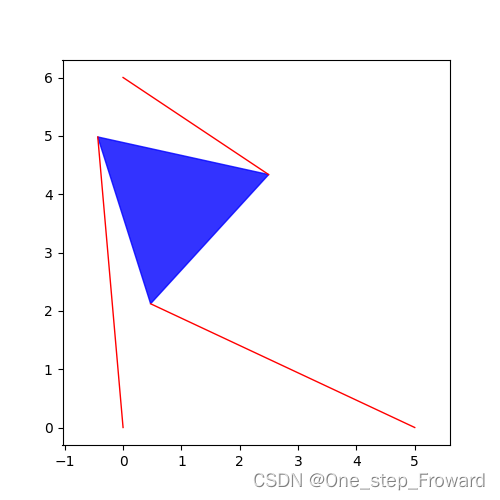可以看出这两组解在数学上都是满足所有条件的。

参考：

Datawhale 数学建模教程