初等数论_1 2016.3.30_给出两个正整数 d 和 s。需要找出两个非负整数 a 和 b,使得同时满足如下条件: 1-CSDN博客

本文链接：https://blog.csdn.net/Only_AiR/article/details/51010018

本文介绍了数论的基础概念，包括整数的性质和最大公约数GCD。重点讲解了扩展欧几里德算法，它用于求解模线性方程，并在求解不定方程中有着广泛应用。还探讨了算法的实现和应用实例，如青蛙的约会问题。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

数论，顾名思义，是对整数进行研究的理论。
是数学学科的一个重要分支，也是ACM竞赛题型中饶有趣味的一个部分。

数论，有人戏称为“素论”。
可见对于素数的研究在数论中比重之大。
当然，也有不是对素数操作的算法，在这里我们也将其划归为数论。

一、整数

1.1
这里写图片描述
1.2
(1)0可以被任何非0数整除
(2)传递性：a | b && b | c <=> a | c.
(3)如果a、b都能被c整除，那么(a+b)或(a-b)也可以被c整除
(4)几个数相乘，如果其中有一个因数能被某一个整除相除，那么它们的积也能被这个数整除。
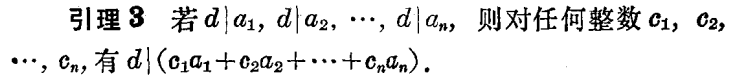
这里写图片描述

几个略实用的性质：
(1)能被2整除的数，个位上的数都能被2整除
(2)能被4整除的数，个位和十位所组成的两位数能被4整除
(3)能被8整除的数，百位、十位和个位所组成的三位数能被8整除
(4)能被5整除的数，末尾是0或5
(5)能被25整除的数，十位和个位所组成的两位数能被25整除
(6)能被125整除的数，百位、十位和个位所组成的三位数能被125整除
(7)能被3整除的数，各个数位上的数字之和能被3整除
(8)能被9整除的数，各个数位上的数字和能被 9 整除
(9)如果一个数既能被 2 整除又能被 3 整除，那么这个数能被 6 整除
(10)如果一个数既能被 2 整除又能被 5 整除，那么这个数能被 10 整除（即个位为0）
(11)能被 11 整除的数，奇数位（从左往右数）上的数字和与偶数位上的数字和的差（大数减小数）能被 11 整除

二、最大公约数GCD（greatest common divisor）

2.1
我们称GCD是a和b的最大公约数，（记为GCD = (a, b)）
当且仅当：
(i) GCD | a， GCD | b
(ii)若c | a, c | b，则c≤GCD

2.2最小公约数LCM（lowest common multiple）

LCM(a, b) = a / GCD(a, b) * b;

如果写成a * b / GCD(a, b)的话，a*b可能会溢出

2.3

定理1 ：
若(a,b) = GCD，则(a/GCD, b/GCD) = 1
若(a, b) = 1，我们就称a和b互素

定理2（除法算式）：
给定正整数a和b，b≠0，存在唯一的整数q和r（其中0 ≤r＜b），
使 a = b*q + r

引理4 ：
若 a = b*q + r，则(a, b) = (b, r)

2.4

定理3（欧几里得（Euclid）算法）（辗转相除法）：
这里写图片描述
若a和b中有一个为负数，我们可以利用
(a, b) = (-a, b) = (a, -b) = (-a, -b)

HDU 1019 Least Common Multiple(最小公倍数)

#include <iostream>
#include <cstdio>
#include <cstring>

using namespace std;

int num[200000];

int Gcd(int a, int b)
{
    return (a%b==0 ? b : Gcd(b, a%b));
}

int main()
{
//    freopen("in.txt", "r", stdin);
    int T;
    while (cin>>T) {
        while (T--) {
            int n;
            cin>>n;
            int Lcm = 0;
            for (int i=0; i<n; ++i) {
                cin>>num[i];
                if (i == 0) {
                    Lcm = num[i];
                } else {
                    if (num[i] < Lcm) {
                        int t = num[i];
                        num[i] = Lcm;
                        Lcm = t;
                    }
                    Lcm = Lcm / Gcd(num[i], Lcm) * num[i];
                }
            }
            cout<<Lcm<<endl;
        }
    }
    return 0;
}

2.5小数的GCD

#include <cmath>

const double eps = 1e-2;

double fgcd(double a, double b)
{
    if (fabs(a) < eps) {
        return b;
    }
    if (fabs(b) < eps) {
        return a;
    }
    return fgcd(b, fmod(a, b));
}

2.6扩展欧几里德算法

扩展欧几里德算法是用来在已知a, b求解一组x，y
使得a * x + b * y = Gcd(a, b)(根据数论中的相关定理，解一定存在)。

扩展欧几里德常用在求解模线性方程及方程组中。

C++实现

#include <iostream>

using namespace std;

#define LL long long

LL x, y;

LL Ext_Gcd(LL a, LL b, LL &x, LL &y);

int main()
{
    LL a, b;

    while (cin>>a>>b) {
        Ext_Gcd(a, b, x, y);
    }
    return 0;
}

LL Ext_Gcd(LL a, LL b, LL &x, LL &y)
{
    if (b == 0) {
        x = 1;
        y = 0;
        return a;
    }
    LL d = Ext_Gcd(b, a%b, x, y);
    LL t = x;
    x = y;
    y = t - a/b*y;
    cout<<"a = "<<a<<" "<<"b = "<<b<<endl;
    cout<<"x = "<<x<<" "<<"y = "<<y<<endl;
    cout<<endl;
    return d;
}

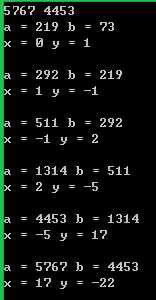
这里写图片描述
把这个实现和Gcd的递归实现相比，发现多了下面的x,y赋值过程，这就是扩展欧几里德算法的精髓。

可以这样思考:

　　对于a’= b， b’= a % b 而言，我们求得 x, y使得 a’x + b’y = Gcd(a’, b’)

　　由于b’ = a % b = a - a / b * b (注：这里的/是程序设计语言中的除法)

那么可以得到:

===> a’x + b’y = Gcd(a’, b’)
===> bx + (a - a / b * b)y = Gcd(a’, b’) = Gcd(a, b)
===> ay + b(x - a / b*y) = Gcd(a, b)

因此对于a和b而言，他们的相对应的p，q分别是 y和(x-a/b*y).

求解 x，y的方法的理解

设 a>b。

1，显然当 b=0，gcd（a，b）=a。此时 x=1，y=0；

2，ab<0 时

设 ax1 + by1 = gcd(a, b);

bx2 + (a%b)y2 = gcd(b, a%b);

根据朴素的欧几里德原理有 gcd(a, b) = gcd(b, a%b);

则:ax1 + by1 = bx2 + (a%b)*y2;

即: ax1 + by1 = bx2 + (a - (a/b)*b )*y2 = ay2 + b(x2-(a/b)y2);

根据恒等定理得：
x1 = y2;
y1 = x2 - (a/b)*y2;

这样我们就得到了求解 x1,y1 的方法：x1，y1 的值基于 x2，y2.

　　上面的思想是以递归定义的，因为 gcd 不断的递归求解一定会有个时候 b=0，所以递归可以结束。

2.7扩展欧几里德算法的应用

(1)求解不定方程：
设过s步后两青蛙相遇，则必满足以下等式：

(x+m*s)-(y+n*s)=k*l(k=0,1,2….)

稍微变一下形得：

(n-m)*s+k*l=x-y

令n-m=a,k=b,x-y=c
即a*s+b*l=c

只要上式存在整数解，则两青蛙能相遇，否则不能。

首先想到的一个方法是用两次for循环来枚举s,l的值，看是否存在s,l的整数解，若存在则输入最小的s，

但显然这种方法是不可取的，谁也不知道最小的s是多大，如果最小的s很大的话，超时是明显的。

这题用欧几里德扩展原理可以很快的解决

步骤如下：
求a * x + b * y = c的整数解。

①、先计算Gcd(a, b)，若c不能被Gcd(a, b)整除，则方程无整数解；
否则，在方程两边同时除以Gcd(a,b)
得到新的不定方程a’* x + b’* y = c’
此时Gcd(a’, b’) = 1

②、利用上面所说的欧几里德算法求出方程a’* x + b’* y = 1的一组整数解x0,y0
则c’* x0,c’* y0是方程a’* x + b’* y = c’的一组整数解；

③、根据数论中的相关定理，可得方程a’ * x + b’ * y = c’的所有整数解为：

其实我们求得的解只是一组，

a*x0 + lcm(a, b) + by0*- lcm(a, b) = 1

a*x + b*y = 1

x=x0+b/gcd(a,b)
y=y0-a/gcd(a,b);

a/gcd(a, b)*x’+ b/gcd(a,b)*y’= c/gcd(a, b)

x’= c/gcd(a,b)*x0 + b/gcd(a,b)
y’= c/gcd(a,b)*y0 - a/gcd(a,b)

x = c’ * x0 + b’ * t

y = c’ * y0 - a’ * t

(t为整数)

上面的解也就是a * x + b * y = n 的全部整数解。

POJ 1061 青蛙的约会

#include <iostream>
#include <cstdio>

using namespace std;

#define LL long long

LL X, Y;

LL Ext_Gcd(LL a, LL b, LL &X, LL &Y);

int main()
{
//    freopen("in.txt", "r", stdin);
    LL x, y, m, n, L;

    while (cin>>x>>y>>m>>n>>L) {
        //(x + m*X) - (y + n*X) = Y*L
        //(n-m)*X + Y*L = x-y
        LL Gcd = Ext_Gcd(n-m, L, X, Y);
        LL t = x-y;
        if (t%Gcd != 0) {
            cout<<"Impossible"<<endl;
        } else {
            //x = c' * x0 + b' * t(t为整数)
            X *= (t/Gcd);
            L /= Gcd;
            if (L < 0) {
                L = -L;
            }
            LL ans = X%L;
            if (ans <= 0) {
                ans += L;
            }
            cout<<ans<<endl;
        }
    }
    return 0;
}

LL Ext_Gcd(LL a, LL b, LL &X, LL &Y)
{
    if (b == 0) {
        X = 1;
        Y = 0;
        return a;
    }
    LL d = Ext_Gcd(b, a%b, X, Y);
    LL t = X;
    X = Y;
    Y = t - a/b*Y;
    return d;
}