桶排序_桶排序 csdn-CSDN博客

转载至：http://blog.csdn.net/cauchyweierstrass/article/details/49919559

桶排序

桶排序(Bucket Sort)假设输入数据服从均匀分布，然后将输入数据均匀地分配到有限数量的桶中，然后对每个桶再分别排序，对每个桶再使用插入排序算法，最后将每个桶中的数据有序的组合起来。前面了解到基数排序假设输入数据属于一个小区间内的整数，而桶排序则是假设输入是由一个随机过程生成，该过程将元素均匀的分布在一个区间[a,b]上。由于桶排序和计数排序一样均对输入的数据进行了某些假设限制，因此比一般的基于比较的排序算法复杂度低。

桶排序过程

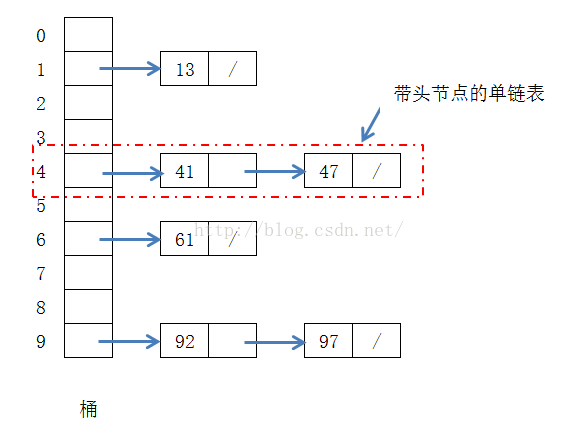
1.初始化装入连续区间元素的n个桶，每个桶用来装一段区间中的元素。

2.遍历待排序的数据，将其映射到对应的桶中，保证每个桶中的元素都在同一个区间范围中。

3.对每个桶进行排序，最终将所有桶中排好序的元素连起来。

桶排序其中也蕴含着分治的策略，联想之前的计数排序，基数排序就像是桶排序的一个特例，一个数据一个桶。并且和散列(哈希，hash)似乎也有千丝万缕的关系。

桶排序的实现

[java] view plain copy

print ?

public int[] buketSort(int[] array, int backetSize) {
int[] result = new int[array.length];
Node[] bucket = new Node[backetSize];
for (int i = 0; i < bucket.length; i++) {
bucket[i] = new Node(); // 带头结点
}
for (int i = 0; i < array.length; i++) {
int bucketIndex = hash(array[i]);
Node node = new Node(array[i]);
Node p = bucket[bucketIndex];
if (p.next == null) {// 没有元素
p.next = node;
} else {// 已经有一个元素
while (p.next != null && p.next.data <= node.data) {
p = p.next;
} // 跳出循环时候该值小于下一个元
node.next = p.next;
p.next = node;
}
}
int j = 0;
for (int i = 0; i < bucket.length; i++) // 确定次数
for (Node p = bucket[i].next; p != null; p = p.next) // n/m
result[j++] = p.data;
return result;
}
private int hash(int value) {
return value / 10;
}

public int[] buketSort(int[] array, int backetSize) {
	int[] result = new int[array.length];
	Node[] bucket = new Node[backetSize];
	for (int i = 0; i < bucket.length; i++) {
		bucket[i] = new Node(); // 带头结点
	}
	for (int i = 0; i < array.length; i++) {
		int bucketIndex = hash(array[i]);
		Node node = new Node(array[i]);
		Node p = bucket[bucketIndex];
		if (p.next == null) {// 没有元素
			p.next = node;
		} else {// 已经有一个元素
			while (p.next != null && p.next.data <= node.data) {
				p = p.next;
			} // 跳出循环时候 该值小于下一个元
			node.next = p.next;
			p.next = node;
		}
	}
	int j = 0;
	for (int i = 0; i < bucket.length; i++) // 确定次数
		for (Node p = bucket[i].next; p != null; p = p.next) // n/m
			result[j++] = p.data;
	return result;
}

private int hash(int value) {
	return value / 10;
}

桶排序的性能

时间消耗包括两部分一部分为初始化桶，连接排好序的桶，其时间复杂度为O(n) 一般有m<n (m个桶)
另一部分为对桶中的元素进行排序，这部分的复杂度，通过代码中的for和while循环直接看不太容易，这样考虑：每个桶里面有ni个元素，对ni个元素进行插入排序的耗时为O(ni^2)。

于是T(n)=O(n)+∑O(ni^2)，平均意义下认为ni=n/m，于是有T(n)=O(n)+n*O((n/m)^2)=O(n^2/m)+O(n)

当n=m时，T(n)=O(n)+O(n)=O(n)

对于每个桶采用其他的排序算法：m个桶，每个桶中的元素平均假设有n/m个，在上面进行基于比较的排序，复杂度不会低于n*O(n/m*lg(n/m))，平均意义下每个桶中的元素有n/m个，O(m * n/m *lg(n/m) = O(n*lg(n/m))，所以总的时间复杂度为T(n)=O(n+n*lg(n/m))

当m=n时时间复杂度为O(n)，此时和计数排序一样，桶数量越多，时间效率越高，然而桶数量越多占用空间也就越大。

如上面后插链表，容易得到桶排序是稳定。

测试

[java] view plain copy

print ?

public static void main(String[] args) {
int[] array = { 15, 90, 25, 76, 47, 58, 32, 67, 84, 26, 12, 3, 9, 56,
98, 51, 79, 47, 39, 67 };
int[] result = buketSort(array, 10);
for (int i : result) {
System.out.print(i + " ");
}
}

public static void main(String[] args) {
	int[] array = { 15, 90, 25, 76, 47, 58, 32, 67, 84, 26, 12, 3, 9, 56,
			98, 51, 79, 47, 39, 67 };
	int[] result = buketSort(array, 10);
	for (int i : result) {
		System.out.print(i + " ");
	}
}

输出

[plain] view plain copy

print ?