文章目录
总结四大排序算法,并对算法领域使用较多的快速排序和归并排序作详细介绍和分析
排序算法的分类:
1插入:插入,折半插入,希尔
2交换:冒泡,快速
3选择:简单选择,堆
4归并:归并(不只二路归并)
5基数:基数排序
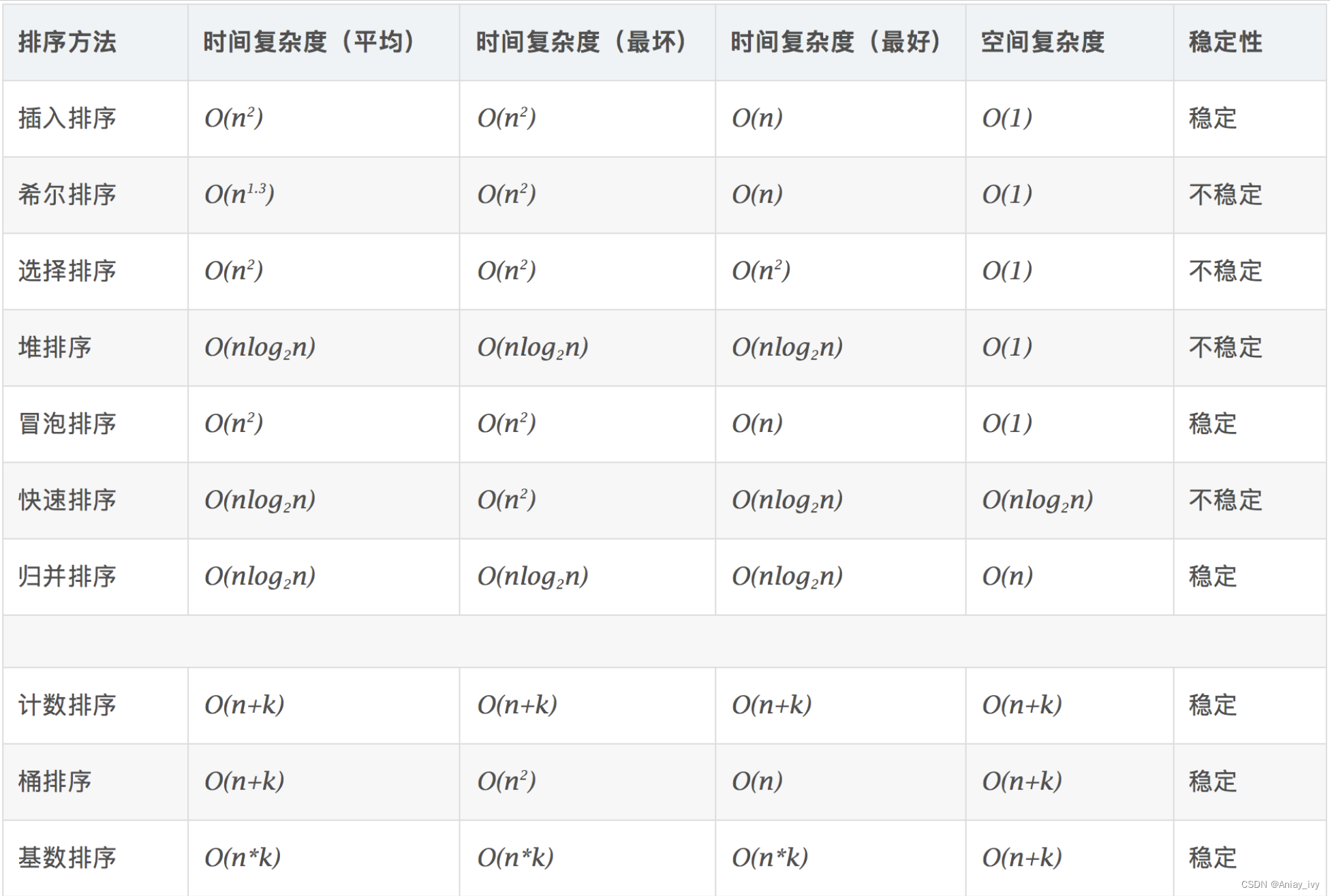
时间复杂度图
1插入排序
void insert_sort()
{
for (int i = 1; i < n; i ++ )
{
int x = a[i];
int j = i-1;
while (j >= 0 && x < a[j])
{
a[j+1] = a[j];
j -- ;
}
a[j+1] = x;
}
}
2选择排序
void select_sort()
{
for (int i = 0; i < n; i ++ )
{
int k = i;
for (int j = i+1; j < n; j ++ )
{
if (a[j] < a[k])
k = j;
}
swap(a[i], a[k]);
}
}
3冒泡排序
void bubble_sort()
{
for (int i = n-1; i >= 1; i -- )
{
bool flag = true;
for (int j = 1; j <= i; j ++ )
if (a[j-1] > a[j])
{
swap(a[j-1], a[j]);
flag = false;
}
if (flag) return;
}
}
4希尔排序
void shell_sort()
{
for (int gap = n >> 1; gap; gap >>= 1)
{
for (int i = gap; i < n; i ++ )
{
int x = a[i];
int j;
for (j = i; j >= gap && a[j-gap] > x; j -= gap)
a[j] = a[j-gap];
a[j] = x;
}
}
}
5快速排序(最快)
void quick_sort(int l, int r)
{
if (l >= r) return ;
int x = a[l+r>>1], i = l-1, j = r+1;
while (i < j)
{
while (a[++ i] < x);
while (a[-- j] > x);
if (i < j) swap(a[i], a[j]);
}
sort(l, j), sort(j+1, r);
}
6归并排序
void merge_sort(int l, int r)
{
if (l >= r) return;
int temp[N];
int mid = l+r>>1;
merge_sort(l, mid), merge_sort(mid+1, r);
int k = 0, i = l, j = mid+1;
while (i <= mid && j <= r)
{
if (a[i] < a[j]) temp[k ++ ] = a[i ++ ];
else temp[k ++ ] = a[j ++ ];
}
while (i <= mid) temp[k ++ ] = a[i ++ ];
while (j <= r) temp[k ++ ] = a[j ++ ];
for (int i = l, j = 0; i <= r; i ++ , j ++ ) a[i] = temp[j];
}
7堆排序
(须知此排序为使用了模拟堆,为了使最后一个非叶子节点的编号为n/2,数组编号从1开始)堆排序详解
void down(int u)
{
int t = u;
if (u<<1 <= n && h[u<<1] < h[t]) t = u<<1;
if ((u<<1|1) <= n && h[u<<1|1] < h[t]) t = u<<1|1;
if (u != t)
{
swap(h[u], h[t]);
down(t);
}
}
int main()
{
for (int i = 1; i <= n; i ++ ) cin >> h[i];
for (int i = n/2; i; i -- ) down(i);
while (true)
{
if (!n) break;
cout << h[1] << ' ';
h[1] = h[n];
n -- ;
down(1);
}
return 0;
}
8基数排序
int maxbit()
{
int maxv = a[0];
for (int i = 1; i < n; i ++ )
if (maxv < a[i])
maxv = a[i];
int cnt = 1;
while (maxv >= 10) maxv /= 10, cnt ++ ;
return cnt;
}
void radixsort()
{
int t = maxbit();
int radix = 1;
for (int i = 1; i <= t; i ++ )
{
for (int j = 0; j < 10; j ++ ) count[j] = 0;
for (int j = 0; j < n; j ++ )
{
int k = (a[j] / radix) % 10;
count[k] ++ ;
}
for (int j = 1; j < 10; j ++ ) count[j] += count[j-1];
for (int j = n-1; j >= 0; j -- )
{
int k = (a[j] / radix) % 10;
temp[count[k]-1] = a[j];
count[k] -- ;
}
for (int j = 0; j < n; j ++ ) a[j] = temp[j];
radix *= 10;
}
}
9计数排序
void counting_sort()
{
int sorted[N];
int maxv = a[0];
for (int i = 1; i < n; i ++ )
if (maxv < a[i])
maxv = a[i];
int count[maxv+1];
for (int i = 0; i < n; i ++ ) count[a[i]] ++ ;
for (int i = 1; i <= maxv; i ++ ) count[i] += count[i-1];
for (int i = n-1; i >= 0; i -- )
{
sorted[count[a[i]]-1] = a[i];
count[a[i]] -- ;
}
for (int i = 0; i < n; i ++ ) a[i] = sorted[i];
}
10桶排序
(基数排序是桶排序的特例,优势是可以处理浮点数和负数,劣势是还要配合别的排序函数)
vector<int> bucketSort(vector<int>& nums) {
int n = nums.size();
int maxv = *max_element(nums.begin(), nums.end());
int minv = *min_element(nums.begin(), nums.end());
int bs = 1000;
int m = (maxv-minv)/bs+1;
vector<vector<int> > bucket(m);
for (int i = 0; i < n; ++i) {
bucket[(nums[i]-minv)/bs].push_back(nums[i]);
}
int idx = 0;
for (int i = 0; i < m; ++i) {
int sz = bucket[i].size();
bucket[i] = quickSort(bucket[i]);
for (int j = 0; j < sz; ++j) {
nums[idx++] = bucket[i][j];
}
}
return nums;
}
快速排序算法的证明与边界分析

算法证明
算法证明使用算法导论里的循环不变式方法
快排模板(以j为分界)
快排属于分治算法,分治算法都有三步:
- 分成子问题
- 递归处理子问题
- 子问题合并
void quick_sort(int q[], int l, int r)
{
//递归的终止情况
if(l >= r) return;
//第一步:分成子问题
int i = l - 1, j = r + 1, x = q[l + r >> 1];
while(i < j)
{
do i++; while(q[i] < x);
do j--; while(q[j] > x);
if(i < j) swap(q[i], q[j]);
}
//第二步:递归处理子问题
quick_sort(q, l, j), quick_sort(q, j + 1, r);
//第三步:子问题合并.快排这一步不需要操作,但归并排序的核心在这一步骤
}
待证问题
while 循环结束后,q[l..j] <= x,q[j+1..r] >= x
q[l..j] <= x意为q[l],q[l+1]...q[j-1],q[j]的所有元素都<= x
证明
循环不变式:q[l..i] <= x q[j..r] >= x
1. 初始化
循环开始之前i = l - 1, j = r + 1则q[l..i],q[j..r]为空,循环不变式显然成立
2. 保持
假设某轮循环开始前循环不变式成立,即q[l..i] <= x, q[j..r] >= x
执行循环体
do i++; while(q[i] < x);
会使得 q[l..i-1] <= x, q[i] >= x
do j--; while(q[j] > x);
会使得 q[j+1..r] >= x, q[j] <= x
if(i < j) swap(q[i], q[j]);
会使得 q[l..i] <= x, q[j..r] >= x
所以,i和j更新之后,下一次循环开始之前,循环不变式依然成立
3. 终止
循环结束时,i >= j
正常情况下,按照循环不变式,我们应该会觉得结果已经显然了
因为i >= j,q[l..i] <= x, q[j..r] >= x
所以按照j来划分的话,q[l..j] <= x, q[j+1..r] >= x是显然的
可是,最后一轮循环有点特殊,因为最后一轮循环的if语句一定不会执行
因为最后一轮循环一定满足 i >= j,不然不会跳出while循环的,所以if语句一定不执行
正确分析:
由于最后一轮的if语句一定不执行
所以,只能保证:
q[l..i-1] <= x, q[i] >= xq[j+1..r] >= x, q[j] <= xi >= j
由q[l..i-1] <= x,i >= j(i-1 >= j-1) 和 q[j] <= x 可以得到 q[l..j] <= x
又因为q[j+1..r] >= x
所以,q[l..j] <= x,q[j+1..r] >= x,问题得证
总结:只有最后一轮循环结束时,循环不变式不成立,其余的循环都是成立的
但最终要求的问题还是解决了
注意:循环结束时要记得检查是否存在数组越界/无限划分的情况
所以还需要证明 j 最终的取值范围是[l..r-1](即不存在n划分成0和n的无限划分情况),分析过程在分析5
边界情况分析
快排属于分治算法,最怕的就是 n分成0和n,或 n分成n和0,这会造成无限划分
分析1
以j为划分时,x不能选q[r]
若以i为划分,则x不能选q[l]
假设 x = q[r]
关键句子quick_sort(q, l, j), quick_sort(q, j + 1, r);
由于j的最小值是l,所以q[j+1…r]不会造成无限划分
但q[l..j](即quick_sort(q, l, j))却可能造成无限划分,因为j可能取到r
举例来说,若x选为q[r],数组中q[l..r-1] < x,
那么这一轮循环结束时i = r, j = r,显然会造成无限划分
分析2
do i++; while(q[i] < x)和do j--; while(q[j] > x) 中不能用q[i] <= x 和 q[j] >= x
假设q[l..r]全相等
则执行完do i++; while(q[i] <= x);之后,i会自增到r+1
然后继续执行q[i] <= x 判断条件,造成数组下标越界(但这貌似不会报错)
并且如果之后的q[i] <= x (此时i > r) 条件也不幸成立,
就会造成一直循环下去(亲身实验),造成内存超限(Memory Limit Exceeded)
现在已经变成 Time Limit Exceeded 了
分析3
if(i < j) swap(q[i], q[j])能否使用 i <= j
可以使用if(i <= j) swap(q[i], q[j]);
因为 i = j 时,交换一下q[i],q[j] 无影响,因为马上就会跳出循环了
分析4
最后一句能否改用quick_sort(q, l, j-1), quick_sort(q, j, r)作为划分
用i做划分时也是同样的道理
不能
根据之前的证明,最后一轮循环可以得到这些结论
q[l..i-1] <= x, q[i] >= xq[j+1..r] >= x, q[j] <= xi >= j
所以,q[l..j-1] <= x 是显然成立的,
但quick_sort(q, j, r)中的q[j] 却是 q[j] <= x,这不符合快排的要求
另外一点,注意quick_sort(q, l, j-1), quick_sort(q, j, r)可能会造成无限划分
当x选为q[l]时会造成无限划分,报错为(MLE),
如果手动改为 x = q[r],可以避免无限划分
但是上面所说的q[j] <= x 的问题依然不能解决,这会造成 WA (Wrong Answer)
分析5
j的取值范围为[l..r-1]
证明:
假设 j 最终的值为 r ,说明只有一轮循环(两轮的话 j 至少会自减两次)
说明q[r] <= x (因为要跳出do-while循环)
说明 i >= r(while循环的结束条件), i 为 r 或 r + 1(必不可能成立)
说明 i 自增到了 r , 说明 q[r] >= x 和 q[l..r-1] < x,
得出 q[r] = x 和 q[l..r-1] < x 的结论,但这与 x = q[l + r >> 1]矛盾
反证法得出 j < r
假设 j 可能小于 l 说明 q[l..r] > x ,矛盾
反证法得出 j >= l
所以 j的取值范围为[l..r-1],不会造成无限划分和数组越界
分析6
while(i < j) 能否改为 while(i <= j)
不能
while(i <= j) 意味着我们认为判断循环结束的条件为 i <= j
那么 if(i < j) 也要改为 if(i <= j)
其实 if(i < j) 改不改都可以, 看完分析 6 后再参考分析 3 可以说明这一点
即
while(i <= j)
{
do i++; while(q[i] < x);
do j--; while(q[j] > x);
if(i <= j) swap(q[i], q[j]);
}
参考循环不变式的证明, 只有最后一轮循环有所不同
我们可以得到:
q[l..i-1] <= x, q[i] >= xq[j+1..r] >= x, q[j] <= xi > j
最终, 我们还能证明出 q[l..j] <= x,q[j+1..r] >= x
也就是说, while(i <= j) 并不会改变循环不变式的部分
但修改后的代码提交后却是 Time Limit Exceeded(TLE), 原因在于无限划分
具体来说, 就是 j 在某些情况下能取到 l-1, 此时就是无限划分
q[l..r] 划分为 q[l..l-1], q[l..r]
某些情况指: 数组只有两个元素 [a, b]且 a < b
这种情况下,
初始 i = l - 1, j = r + 1
第一轮 while 循环结束 i = l, j = l
第二轮 while 循环结束 i = r, j = l-1
于是 while(i <= j) 就造成了无限划分, 而 while(i < j) 就不会造成这个问题, 因为第一轮 while 循环结束后就跳出去了
所以, 不能用 while(i <= j)
有些人可能会疑惑: 这种情况看起来比较极端啊, 如果构造数组 [3, 2, 1] 会不会就不会遇到这种情况了
其实不然, 因为快排是分治算法, 往下递归时总会遇到 [a, b], a < b 这种情况
只要有一个这种情况, 就会进入无限划分出不来.
只有在数组元素全相等情况下才遇不到这种情况, 此时算法就能正常运行了, 读者可自行验证
分析7
循环不变式证明过程中
do i++; while(q[i] < x);
会使得 q[l..i-1] <= x, q[i] >= x
会使得 q[l..i-1] <= x, q[i] >= x 能否改为 会使得 q[l..i-1] < x, q[i] >= x
不能
这里的 q[l..i-1] <= x 是配合循环不变式 q[l..i] <= x q[j..r] >= x 的
于是问题就变成了循环不变式中 q[l..i] <= x 能否改为 q[l..i] < x
假定循环不变式是 q[l..i] < x, q[j..r] > x
执行两个 do-while 循环
do i++; while(q[i] < x);
会使得 q[l..i-1] < x, q[i] >= x
do j--; while(q[j] > x);
会使得 q[j+1..r] > x, q[j] <= x
则执行 if 语句后
if(i < j) swap(q[i], q[j]);
就会变成 q[l..i] <= x, q[j..r] >= x, 与假设矛盾
所以, 考虑最全面的描述还是要带上 = 的
分析8
使用 do-while 循环的好处
好处在于循环变量 i和j 一定更新, 循环不会卡死
如果使用while循环, i和j 在特殊情况下不更新的话,循环就会卡死
例:
while(q[i] < x) i++;
while(q[j] > x) j--;
当q[i]和q[j]都为 x 时, i 和 j 都不会更新,导致 while 陷入死循环
其余模板
用i做划分时的模板
// 从小到大
void quick_sort(int q[], int l, int r)
{
if(l >= r) return;
int i = l - 1, j = r + 1, x = q[l + r + 1 >> 1];//注意是向上取整,因为向下取整可能使得x取到q[l]
while(i < j)
{
do i++; while(q[i] < x);
do j--; while(q[j] > x);
if(i < j) swap(q[i], q[j]);
}
quick_sort(q, l, i - 1), quick_sort(q, i, r);//不用q[l..i],q[i+1..r]划分的道理和分析4中j的情况一样
}
// 从大到小(只改两个判断符号)
void quick_sort(int q[], int l, int r)
{
if(l >= r) return;
int i = l - 1, j = r + 1, x = q[l + r >> 1];
while(i < j)
{
do i++; while(q[i] > x); // 这里和下面
do j--; while(q[j] < x); // 这行的判断条件改一下
if(i < j) swap(q[i], q[j]);
}
quick_sort(q, l, j), quick_sort(q, j + 1, r);
}
Java代码
import java.util.*;
public class Main{
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[] q = new int[n];
for(int i=0; i<n; i++){q[i] = sc.nextInt();}
quickSort(q, 0, n-1);
for(int i=0; i<n; i++){System.out.print(q[i] + " ");}
}
public static void quickSort(int[] q, int l, int r){
if(l >= r) return;
int x = q[l + r >> 1], i = l - 1, j = r + 1;
while(i < j){
while( q[++i] < x );
while( q[--j] > x) ;
if(i < j){
int t = q[i];
q[i] = q[j];
q[j] = t;
}
}
quickSort(q, l, j);
quickSort(q, j + 1, r);
}
}
总结快排思路
- 有数组
q,左端点l,右端点r - 确定划分边界
x - 将
q分为<=x和>=x的两个小数组 i的含义:i之前的元素都≤x,即q[l..i−1] ≤xj的含义:j之后的元素都≥x,即q[j+1..r] ≥x- 结论:
while循环结束后,q[l..j]≤x,q[j+1..r] ≥x - 简单不严谨证明:
while循环结束时, i ≥ j
若 i > j , 显然成立
若 i = j
∵最后一轮循环中两个 do−while 循环条件都不成立
∴ q[i] ≥ x,q[j] ≤ x
∴q[i] = q[j] = x
∴ 结论成立 - 递归处理两个小数组
归并排序的证明与边界分析
算法处理
归并排序,它有两大核心操作.
一个是将数组一分为二,一个无序的数组成为两个数组.
另外一个操作就是合二为一,将两个有序数组合并成为一个有序数组

归并模板
归并属于分治算法,有三个步骤
void merge_sort(int q[], int l, int r)
{
//递归的终止情况
if(l >= r) return;
//第一步:分成子问题
int mid = l + r >> 1;
//第二步:递归处理子问题
merge_sort(q, l, mid ), merge_sort(q, mid + 1, r);
//第三步:合并子问题
int k = 0, i = l, j = mid + 1, tmp[r - l + 1];
while(i <= mid && j <= r)
if(q[i] <= q[j]) tmp[k++] = q[i++];
else tmp[k++] = q[j++];
while(i <= mid) tmp[k++] = q[i++];
while(j <= r) tmp[k++] = q[j++];
for(k = 0, i = l; i <= r; k++, i++) q[i] = tmp[k];
}
待证问题: tmp 保存的是 q[l..mid] , q[mid+1..r] 中从小到大排序的所有数
证明(第一个 while 循环)
循环不变式: tmp[0..k-1] 保存上述俩数组中从小到大排序的最小 k 个数
-
初始
k = 0, tmp[0..k-1]为空,显然成立 -
保持
假设某轮循环开始之前,循环不变式成立
若q[i] <= q[j], 则tmp[k] = q[i]
其中,q[i] <= q[i+1..mid], q[i] <= q[j] <= q[j+1..r]
∴q[i]是剩下的所有数中最小的一个
当q[i] > q[j]时,同理可以得到tmp[k] = q[j]是剩下数中最小的一个
∴tmp[k]是剩下数中最小的一个
∴k自增之后,下轮循环开始之前,tmp[0..k-1]保存从小到大排序的最小k个数 -
终止
i > mid或j > r
则q[l..mid]和q[mid+1..r]其中一个数组的数都已遍历
tmp[0..k-1]保存从小到大排序的最小k个数
边界分析
- 为什么不用
mid - 1作为分隔线呢
即merge_sort(q, l, mid - 1 ), merge_sort(q, mid, r)
因为mid = l + r >> 1是向下取整,mid有可能取到l(数组只有两个数时),造成无限划分
解决办法:mid向上取整就可以了, 即mid = l + r + 1 >> 1,如下所示:
void merge_sort(int q[], int l, int r)
{
if(l >= r) return;
int mid = l + r + 1>> 1;//注意mid是向上取整
merge_sort(q, l, mid - 1 ), merge_sort(q, mid, r);
int k = 0, i = l, j = mid, tmp[r - l + 1];
while(i < mid && j <= r)
if(q[i] <= q[j]) tmp[k++] = q[i++];
else tmp[k++] = q[j++];
while(i < mid) tmp[k++] = q[i++];
while(j <= r) tmp[k++] = q[j++];
for(k = 0, i = l; i <= r; k++, i++) q[i] = tmp[k];
}
不过最好不要这样写,很奇葩,不对称
- 为什么 用
mid作为分隔线时不会造成无限划分呢
因为此时mid是向下取整的,merge_sort(q, l, mid )中的mid一定不会取到r值
∴merge_sort(q, l, mid )不会无限划分
Java模板
import java.util.Scanner;
public class Main{
public static void main(String[] args){
Scanner s = new Scanner(System.in);
int n = s.nextInt();
int[] arr = new int[n];
for(int i = 0;i < arr.length;i++){
arr[i] = s.nextInt();
}
mergeSort(arr,0,n-1);
for(int i = 0;i < arr.length;i++){
System.out.print(arr[i] + " ");
}
}
public static void mergeSort(int[] arr,int left,int right){
if(left >= right) return;
int mid = (left + right) / 2;
mergeSort(arr,left,mid);
mergeSort(arr,mid + 1,right);
int[] temp = new int[right - left + 1];
int k = 0,i = left,j = mid + 1;
while(i <= mid && j <= right)
if(arr[i] <= arr[j])
temp[k ++ ] = arr[i ++ ];
else
temp[k ++ ] = arr[j ++ ];
while(i <= mid)
temp[k ++ ] = arr[i ++ ];
while(j <= right)
temp[k ++ ] = arr[j ++ ];
for(i = left,j = 0;i <= right;i++,j++)
arr[i] = temp[j];
}
}
摊还分析
摊还分析是一种分析时间复杂度的方法
主要有三种:
- 聚合分析(记账法)
- 核方法
- 势能法
聚合分析(记账法)最符合直观感觉,
聚合分析归并排序的时间复杂度
归并排序属于分治法, 很容易写出递归式:
T(n) = 2T( n / 2 ) + f(n)
其中, 2T( n / 2 ) 是子问题的时间复杂度, f(n)是合并子问题的时间复杂度
1.直观
直观上我们感觉 f(n)=O(n), 事实也正是如何, 因为每次 while 都会把一个元素添加到数组中, 一共有 n 个元素, 所以 while 循环的次数为 n , 时间复杂度为 O(n)
2.摊还分析的聚合分析
对于每次迭代中选出并添加到数组中的元素, 我们给它的摊还代价设为 1(记账为 1)
一个元素只能计费一次, 因为马上就被添加到数组中了
一共有 n 个元素, 所以摊还总代价为 n, 算法的时间复杂度为 O(n)
摊还代价, 我们自己设定的一个理想代价, 只有一个要求: 总的摊还代价大于总的实际代价, 所以总摊还代价是总实际代价的上界 实际代价,
实际操作的代价
3.计算归并排序的递归式
得到 f(n)=O(n)
后, 根据递推式的计算方法(代入法, 递归树法, 主方法)容易计算出 T(n)=O(n log n), 即归并排序的时间复杂度为 O(n log n)
总结归并思路
-
有数组 q, 左端点 l, 右端点 r
-
确定划分边界 mid
-
递归处理子问题 q[l…mid], q[mid+1…r]
-
合并子问题
-
主体合并
至少有一个小数组添加到 tmp 数组中 -
收尾
可能存在的剩下的一个小数组的尾部直接添加到 tmp 数组中 -
复制回来
tmp 数组覆盖原数组

























 110
110











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








