论文名称:Deep Gaussian Embedding of Graphs: Unsupervised Inductive Learning via Ranking
论文下载地址:https://arxiv.org/abs/1707.03815
数据集、源码和其他附件下载地址:https://www.kdd.in.tum.de/g2g
本文是2018年ICLR论文,关注无监督inductive图表征学习任务(利用新节点的特征信息实现表征),可以处理plain/attributed, directed/undirected的场景。
本文认为,以前的工作都将节点嵌入为低维连续空间的point vectors,而本文将其嵌入为高斯分布
h
i
=
N
(
µ
i
,
Σ
i
)
\mathbf{h}_i =\mathcal{N}(µ_i, Σ_i)
hi=N(µi,Σi),以捕获表征中的不确定性(通过对其的分析,可以估计neighborhood diversity、检测图的intrinsic latent dimensionality)。
G2G使用personalized ranking formulation,利用网络结构中节点的自然顺序(跳-距离,应当同序)。
1. Uncertainty的重要性

2. G2G
- 表征节点特征,返回节点嵌入分布相关的参数
- 无监督损失函数→网络结构中节点的自然顺序→基于嵌入分布的不相似度量(这一步是用来将结构信息隐式学到表征中)
h
i
=
N
(
µ
i
,
Σ
i
)
\mathbf{h}_i =\mathcal{N}(µ_i, Σ_i)
hi=N(µi,Σi)
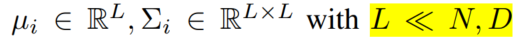
(N是节点数,D是初始特征维度)
嵌入目标:图中相似的节点,在嵌入域表征相似
personalized ranking formulation
利用节点的k跳邻居,对它们的嵌入与节点嵌入的距离进行排序
节点
i
i
i 的k跳邻居:

我们希望的是,邻居节点们的跳数,和它与目标节点在向量域嵌入的距离,有相同的排序关系:

即遵从这样的pairwise constraints:

超过一二阶相似度,得到局部和全局的多尺度结构
向量之间的不相似度量:
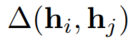
因为本文的隐表示是分布,所以用不对称的KL散度(也对处理有向图有利):

2.1 第一部分:encoder
高斯分布中的 μ \mu μ和 Σ \Sigma Σ→先过一个 f θ f_\theta fθ,然后用其最后一层输入 μ \mu μ和 Σ \Sigma Σ
要diagonal covariance matrices

(呃其实这段我没看懂是啥意思!)
附录有介绍具体表征用的模型
2.2 第二部分:无监督损失函数
基于energy-based loss
penalizes ranking errors given the energy of the pairs(两个节点之间的KL散度就是energy)
square-exponential loss
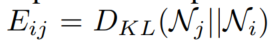

valid三元组:

抽样策略(直接用正态分布可能导致低度数节点少)alternative node-anchored sampling strategy(细节待补)

附录有介绍与其他高斯嵌入方法的不同之处
3. 实验
其他略。做了链路预测和节点分类任务。测试了不同抽样策略,测试节点表征不确定性,测试inductive learning效果,做表征可视化,对特征encoder做了ablation study
附录还介绍了无法处理训练集中未出现过的节点的方法的edge cover问题








 本文探讨了一种无监督的图表征学习方法——DeepGaussianEmbedding,它将节点嵌入表示为高斯分布,以捕捉不确定性。通过个性化排名形式化,利用节点的k跳邻居进行排序,实现多尺度结构学习。实验涉及链接预测和节点分类任务,证明了该方法在inductive learning中的有效性。
本文探讨了一种无监督的图表征学习方法——DeepGaussianEmbedding,它将节点嵌入表示为高斯分布,以捕捉不确定性。通过个性化排名形式化,利用节点的k跳邻居进行排序,实现多尺度结构学习。实验涉及链接预测和节点分类任务,证明了该方法在inductive learning中的有效性。


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










