torch.linalg.norm在不同维度的张量上给出的结果不同：探讨原因与解决方案

诸神缄默不语-个人CSDN博文目录

（我用的版本：Python 3.8.13; PyTorch 1.11.0）

计算张量大小时用的是L2范数，很直觉地会想到用torch.linalg.norm，然后发现不同维度的张量会给出不同的答案：
（c是拿来对比用的，我一开始主要只考虑a和b的问题）

import torch
from torch import linalg as LA

a=torch.arange(8).float()
b=a.reshape(4,2)
c=a.reshape(-1,1)
print(LA.norm(a,ord=2))
print(LA.norm(b,ord=2))
print(LA.norm(c,ord=2))

输出：

tensor(11.8322)
tensor(11.8079)
tensor(11.8322)

问了一下ChatGPT，说可能是因为浮点精度的问题，但是最后也没解释清楚到底为啥（ChatGPT什么时候加速赶紧替代我吧，这种问题怎么还要我自己去搜索解决方案啊），所以我就自己去查了官方API文档：torch.linalg.norm — PyTorch 2.0 documentation

torch.linalg.norm(A, ord=None, dim=None, keepdim=False, *, out=None, dtype=None) → Tensor

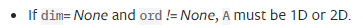
ord入参指定了计算范式，在这里我们本来是想算L2范式的，所以选择2：

对于一维向量，算法显然就是传统的L2范式（$\sqrt{\sum |x{|}^2}$）；但对于二维矩阵，这里算的却是最大奇异值。
事实上矩阵的二范数就等于其最大奇异值，但是具体怎么推导的我也不知道，我也没学，可以参考这篇博文¹。总之从这篇博文中我们知道最大奇异值是$A^{T}A$的最大特征值的平方根。
但是代码得到的结果不同，于是我们自然猜测是这两种计算方法导致结果不同，于是我们手算：

import torch
from torch import linalg as LA

import math

a=torch.arange(8).float()
print(LA.norm(a,ord=2))
print(math.sqrt(1**2+2**2+3**2+4**2+5**2+6**2+7**2))

b=a.reshape(4,2)
print(LA.norm(b,ord=2))
(evals,evecs) = torch.eig(torch.mm((b.T),b),eigenvectors=True)
print(torch.max(evals))
print(math.sqrt(torch.max(evals)))

c=a.reshape(-1,1)
(evals,evecs) = torch.eig(torch.mm((c.T),c),eigenvectors=True)
print(torch.max(evals))
print(math.sqrt(torch.max(evals)))

输出：

tensor(11.8322)
11.832159566199232
tensor(11.8079)
this_file.py:12: UserWarning: torch.eig is deprecated in favor of torch.linalg.eig and will be removed in a future PyTorch release.
torch.linalg.eig returns complex tensors of dtype cfloat or cdouble rather than real tensors mimicking complex tensors.
L, _ = torch.eig(A)
should be replaced with
L_complex = torch.linalg.eigvals(A)
and
L, V = torch.eig(A, eigenvectors=True)
should be replaced with
L_complex, V_complex = torch.linalg.eig(A) (Triggered internally at  /opt/conda/conda-bld/pytorch_1646755853042/work/aten/src/ATen/native/BatchLinearAlgebra.cpp:2910.)
  (evals,evecs) = torch.eig(torch.mm((b.T),b),eigenvectors=True)
tensor(139.4262)
11.807888200473563
tensor(140.)
11.832159566199232

这样就能很明显看出二者之间因精度而产生的差异了。

解决方案：如果你就是想算标准的L2范式，请把张量直接改成一维向量。

其他本文撰写过程中参考的网络资料：

1. pytorch中的矩阵乘法：函数mul,mm,mv以及 @运算 和 *运算_柏常青的博客-CSDN博客（我一直都分不清谁是干啥的……）
2. 特征值的最大值与最小值 - 知乎
3. Pytorch之线性代数 - 简书

---

1. 矩阵的二范数为何等于其奇异值 - EpsAvlc的博客 ↩︎