小白也能看懂的 ROC 曲线详解

作者：PrimiHub-Kevin

ROC 曲线是一种坐标图式的分析工具，是由二战中的电子和雷达工程师发明的，发明之初是用来侦测敌军飞机、船舰，后来被应用于医学、生物学、犯罪心理学。

如今，ROC 曲线已经被广泛应用于机器学习领域的模型评估，说到这里就不得不提到 Tom Fawcett 大佬，他一直在致力于推广 ROC 在机器学习领域的应用，他发布的论文《An introduction to ROC analysis》更是被奉为 ROC 的经典之作（引用 2.2w 次），知名机器学习库 scikit-learn 中的 ROC 算法就是参考此论文实现，可见其影响力！

不知道大多数人是否和我一样，对于 ROC 曲线的理解只停留在调用 scikit-learn 库的函数，对于它的背后原理和公式所知甚少。

前几天我重读了《An introduction to ROC analysis》终于将 ROC 曲线彻底搞清楚了，独乐乐不如众乐乐！如果你也对 ROC 的算法及实现感兴趣，不妨花些时间看完全文，相信你一定会有所收获！

一、什么是 ROC 曲线

下图中的蓝色曲线就是 ROC 曲线，它常被用来评价二值分类器的优劣，即评估模型预测的准确度。

二值分类器，就是字面意思它会将数据分成两个类别(正/负样本)。例如：预测银行用户是否会违约、内容分为违规和不违规，以及广告过滤、图片分类等场景。篇幅关系这里不做多分类 ROC 的讲解。

坐标系中纵轴为 TPR（真阳率/命中率/召回率）最大值为 1，横轴为 FPR（假阳率/误判率）最大值为 1，虚线为基准线（最低标准），蓝色的曲线就是 ROC 曲线。其中 ROC 曲线距离基准线越远，则说明该模型的预测效果越好。(TPR: True positive rate; FPR: False positive rate)

• ROC 曲线接近左上角：模型预测准确率很高
• ROC 曲线略高于基准线：模型预测准确率一般
• ROC 低于基准线：模型未达到最低标准，无法使用

二、背景知识

考虑一个二分类模型， 负样本(Negative) 为 0，正样本(Positive) 为 1。即：

• 标签 $y$ 的取值为 0 或 1。
• 模型预测的标签为 $\hat{y}$，取值也是 0 或 1。

因此，将 $y$ 与 $\hat{y}$ 两两组合就会得到 4 种可能性，分别称为：

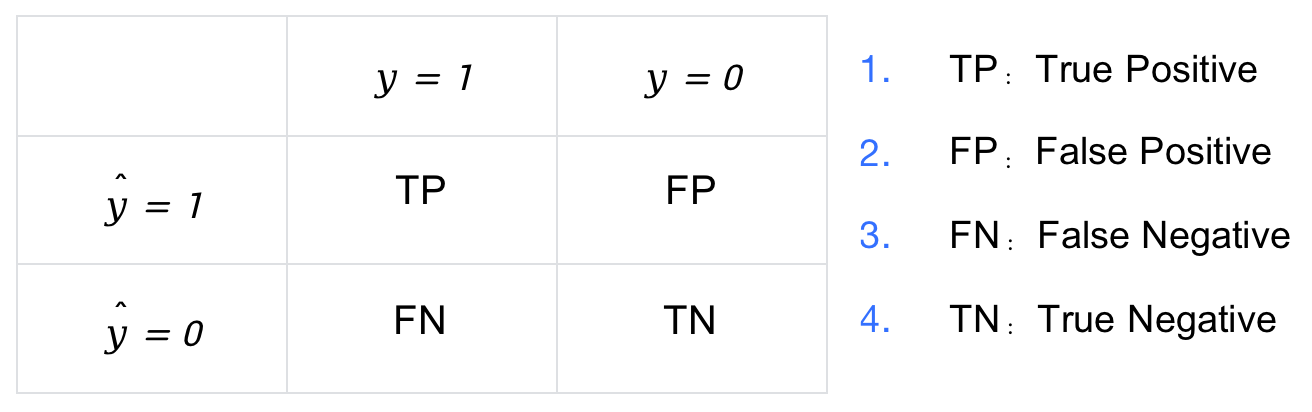
2.1 公式

ROC 曲线的横坐标为 FPR（False Positive Rate），纵坐标为 TPR（True Positive Rate）。FPR 统计了所有负样本中 预测错误(FP) 的比例，TPR 统计了所有正样本中 预测正确(TP) 的比例，其计算公式如下，其中 # 表示统计个数，例如 #N 表示负样本的个数，#P 表示正样本的个数

$\text{FPR}=\frac{\#\text{FP}}{\#\text{N}}$，$\text{TPR}=\frac{\#\text{TP}}{\#\text{P}}$

2.