快速幂的类比应用

快速幂：用乘法实现乘方

快速加：用乘法实现加法

快速幂的本质是：a*a*a*...*a%mod

快速加：(a+a+a+...+a)%mod

额外知识点：（a+b）%c  =  （a%c+b%c）%c

题目：计算a*b%p

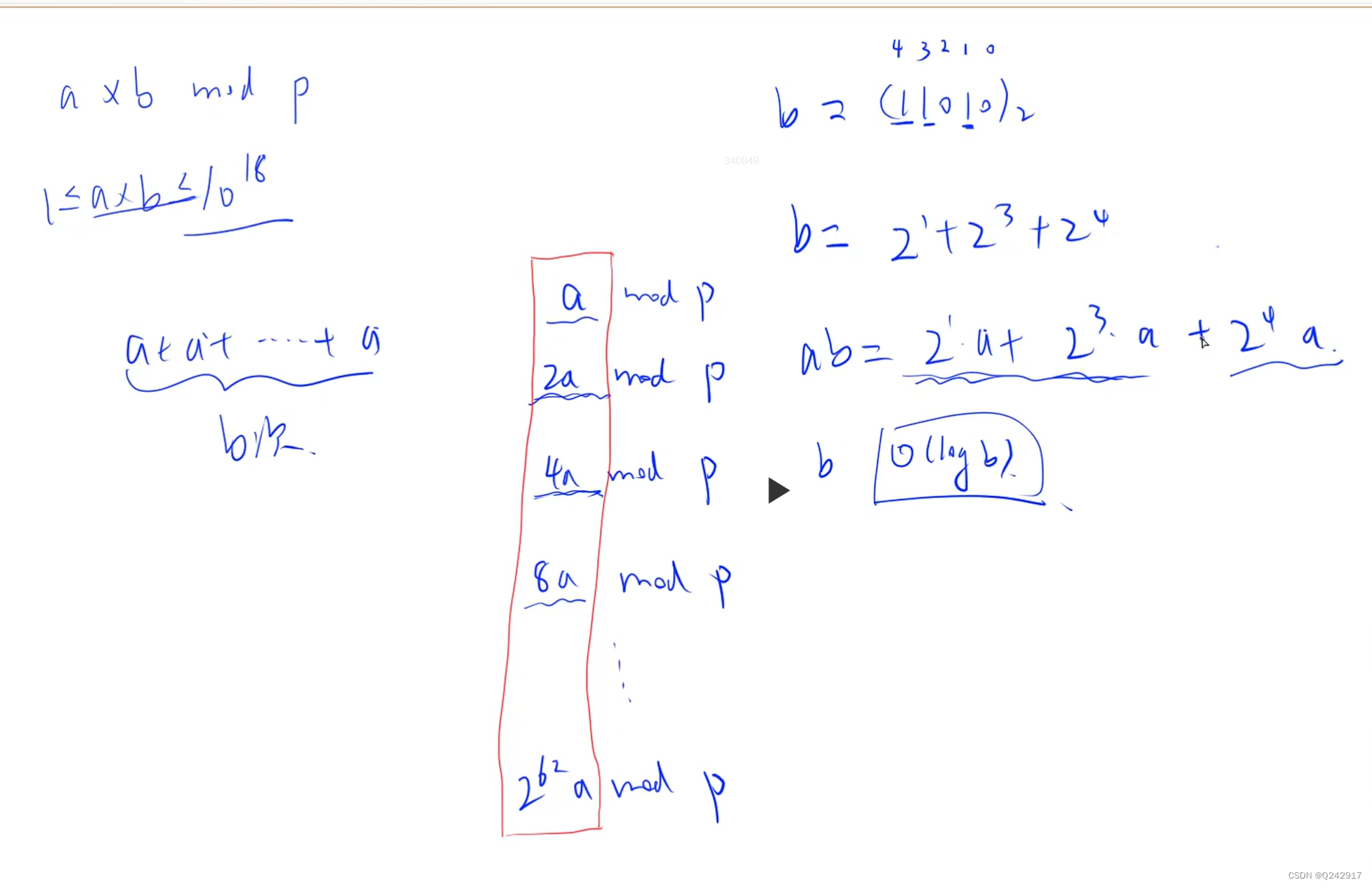
//看成b个a相加，将b个a分解成a，2a，4a，8a...分别求出每一个
// Created by 86151 on 2024/6/19.
//把b转为二进制表示
#include <iostream>
using namespace std;
#define LL long long

//计算a*b%p
LL qadd(LL a,LL b,LL p){
    //转换为b个a相加
    LL res = 0;
    while(b!=0){
        if(b&1) res = (res+a)%p;//如果b对应的二进制末尾是1


        a = (a%p+a%p)%p;//位权变为更高一位的
        b>>=1;
    }
    return res;
}

int main(){
    LL a,b,p;
    cin>>a>>b>>p;
    cout<<qadd(a,b,p);
    return 0;
}

（附快速幂代码）

//两个1e9的数相乘会爆int
// Created by 86151 on 2024/6/19.
//这里写到的所有LL都很重要，如果不加就会产生错误
#include <iostream>
using namespace std;
#define LL long long
int t;

//a的b次方%p
int qmi(int a,int b,int p){
    //看成b个a相乘
    //b个<==>b的二进制表示
    LL res = 1;
    while(b){
        if(b&1) res = (LL)res*a%p;

        a = (LL)a*a%p;
        b>>=1;
    }
    return res;
}

int main(){
    cin>>t;
    while(t--){
        int a,b,p;
        cin>>a>>b>>p;
        cout<<qmi(a,b,p)<<endl;
    }
    return 0;
}