0-1 背包问题

描述

给你一个可装载重量为W的背包和N个物品，每个物品有重量和价值两个属性。其中第i个物品的重量为w[i]，价值为v[i]，现在让你用这个背包装物品，最多能装的价值是多少？

这是最基础的背包问题，特点是：每种物品仅有一件，可以选择放或不放。

题目就是这么简单，一个典型的动态规划问题。这个题目中的物品不可以分割，要么装进包里，要么不装，不能说切成两块装一半。这就是 0-1 背包这个名词的来历。

解决这个问题没有什么排序之类巧妙的方法，只能穷举所有可能，根据我们「动态规划详解」中的套路，直接走流程就行了。

动规标准套路

第一步要明确两点，「状态」和「选择」。

先说状态，如何才能描述一个问题局面？只要给几个物品和一个背包的容量限制，就形成了一个背包问题呀。所以状态有两个，就是「背包的容量」和「可选择的物品」。

再说选择，也很容易想到啊，对于每件物品，你能选择什么？选择就是「装进背包」或者「不装进背包」嘛。

明白了状态和选择，动态规划问题基本上就解决了，只要往这个框架套就完事儿了：

for 状态1 in 状态1的所有取值：
    for 状态2 in 状态2的所有取值：
        for ...
            dp[状态1][状态2][...] = 择优(选择1，选择2...)

PS：此框架出自历史文章 团灭 LeetCode 股票问题。

第二步要明确 dp 数组的定义。

首先看看刚才找到的「状态」，有两个，也就是说我们需要一个二维dp数组。

dp[i][w]的定义如下：对于前i个物品，当前背包的容量为w，这种情况下可以装的最大价值是dp[i][w]。

比如说，如果dp[3][5] = 6，其含义为：对于给定的一系列物品中，若只对前 3 个物品进行选择，当背包容量为 5 时，最多可以装下的价值为 6。

PS：为什么要这么定义？便于状态转移，或者说这就是套路，记下来就行了。建议看一下我们的动态规划系列文章，几种套路都被扒得清清楚楚了。

根据这个定义，我们想求的最终答案就是dp[N][W]。base case 就是dp[0][..] = dp[..][0] = 0，因为没有物品或者背包没有空间的时候，能装的最大价值就是 0。

细化上面的框架：

int dp[N+1][W+1]
dp[0][..] = 0
dp[..][0] = 0

for i in [1..N]:
    for w in [1..W]:
        dp[i][w] = max(
            把物品 i 装进背包,
            不把物品 i 装进背包
        )
return dp[N][W]

第三步，根据「选择」，思考状态转移的逻辑。

简单说就是，上面伪码中「把物品 i 装进背包」和「不把物品 i 装进背包」怎么用代码体现出来呢？

这就要结合对 dp 数组的定义和我们的算法逻辑来分析了：

先重申一下刚才我们的 dp 数组的定义：

dp[i][w]表示：对于前i个物品，当前背包的容量为w时，这种情况下可以装下的最大价值是dp[i][w]。

如果你没有把这第i个物品装入背包，那么很显然，最大价值dp[i][w]应该等于dp[i-1][w]，继承之前的结果。

如果你把这第i个物品装入了背包，那么dp[i][w]应该等于dp[i-1][w - w[i-1]] + v[i-1]。

首先，由于i是从 1 开始的，所以 v 和 w 的索引是i-1时表示第i个物品的价值和重量。

而dp[i-1][w - w[i-1]]也很好理解：你如果装了第i个物品，就要寻求剩余重量w - w[i-1]限制下的最大价值，加上第i个物品的价值v[i-1]。

综上就是两种选择，我们都已经分析完毕，也就是写出来了状态转移方程，可以进一步细化代码：

for i in [1..N]:
    for w in [1..W]:
        dp[i][w] = max(
            dp[i-1][w],
            dp[i-1][w - w[i-1]] + v[i-1]
        )
return dp[N][W]

最后一步，把伪码翻译成代码，处理一些边界情况。

//wt和val的长度都为N
    int knapsack(int W, int N, LinkedList<Integer> wt, LinkedList<Integer> val) {
        // base case
        int[][] dp = new int[N + 1][W + 1];
        
        for (int i = 1; i <= N; i++) {
            for (int w = 1; w <= W; w++) {
                if (w - wt.get(i-1) < 0) {
                    // 这种情况下只能选择不装入背包
                    dp[i][w] = dp[i - 1][w];
                } else {
                    // 装入或者不装入背包，择优
                    dp[i][w] = Math.max(dp[i - 1][w - wt.get(i-1)] + val.get(i-1),
                            dp[i - 1][w]);
                }
            }
        }
        return dp[N][W];
    }

优化方法

由于dp[i][v] 是二维的，所以我们可以使用 二维数组 实现，时间复杂度和空间复杂度均为 O(nV)。伪代码如下：

int knapsack2(int W, int N, int[] wt, int[] val) {
	//现在dp[i]是在重量<=i的情况下的最大价值
	int[] dp = new int[N + 1];

    for (int i = 1; i <= N; i++) {
		for (int w = W; w >= wt[i - 1]; w--) {
			dp[w] = Math.max(dp[w - wt[i-1]] + val[i-1], dp[w]);
		}
	}
	return dp[W];
}

为什么能这样优化呢？这里理解起来比较困难，希望你集中注意力，我们来一起分析一下。

首先，在优化前，根据代码来看，二维数组是这样填满的：

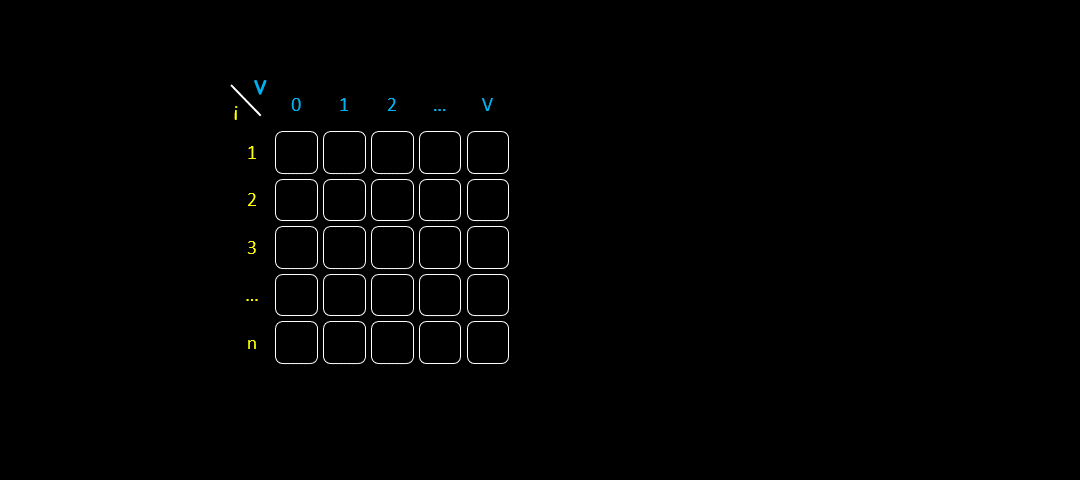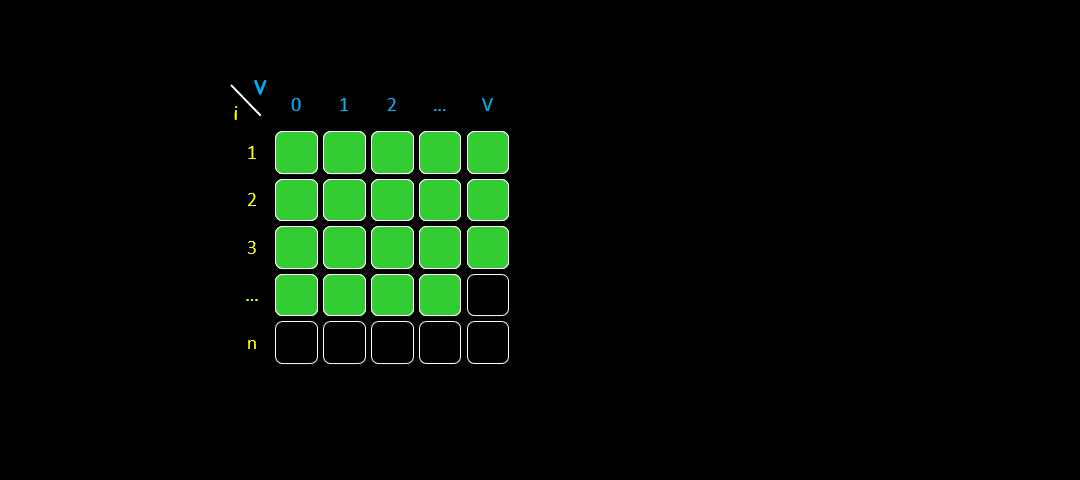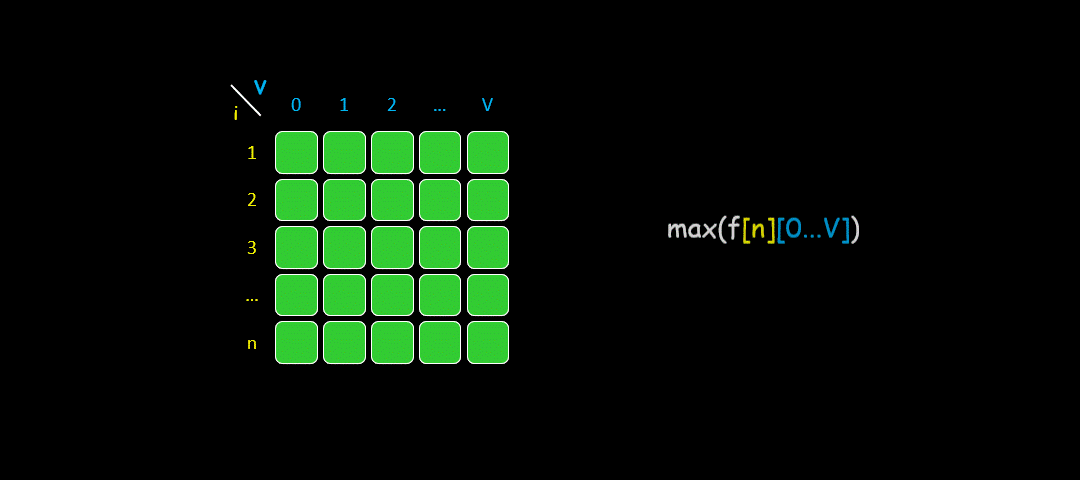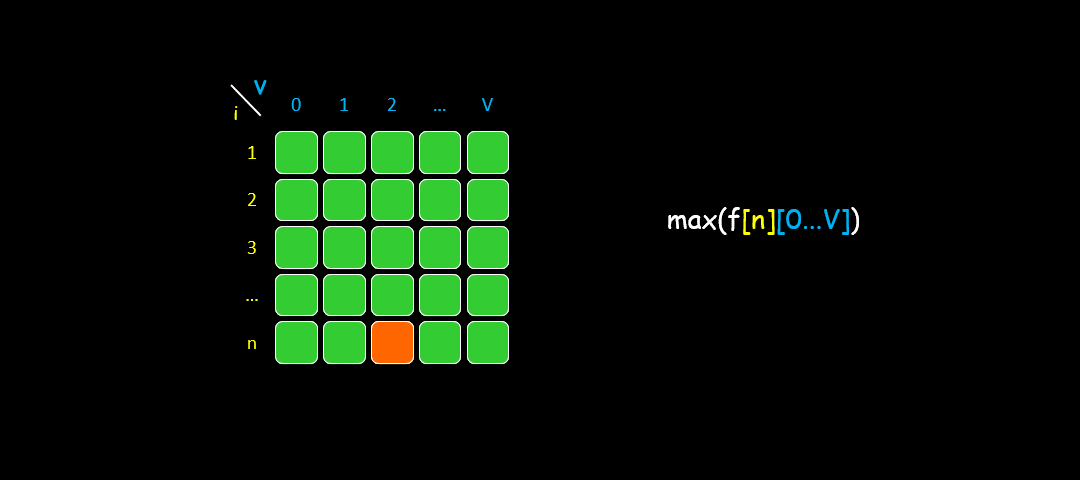
二维数组转换为一维数组大致示意图如下：

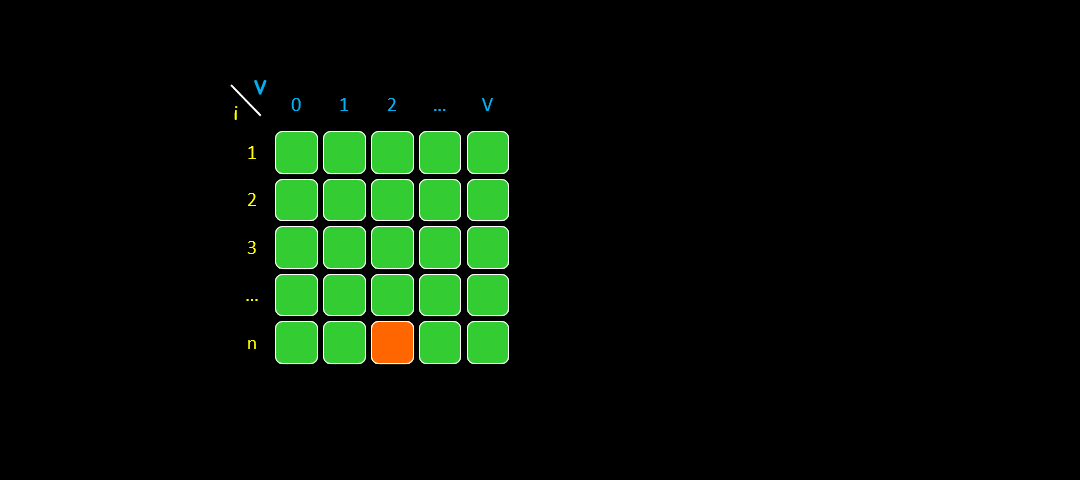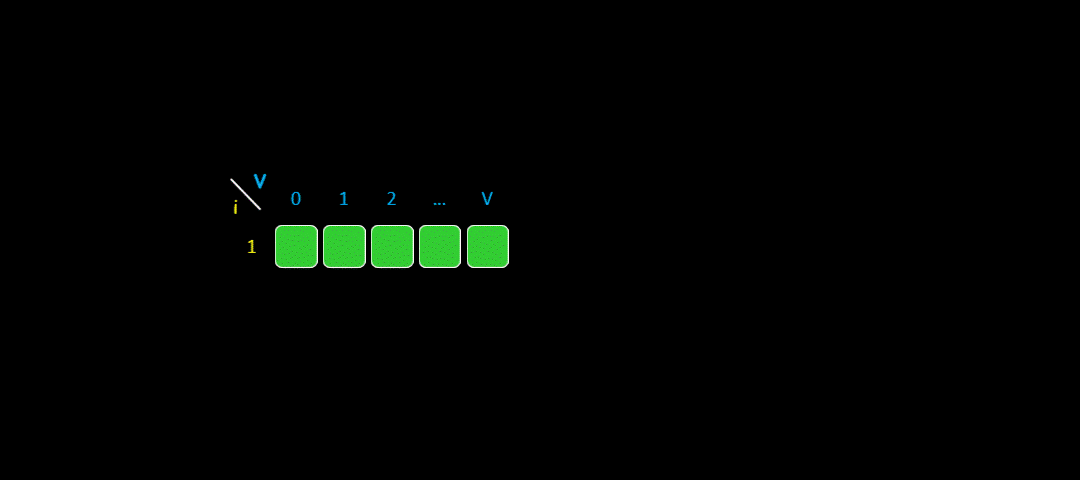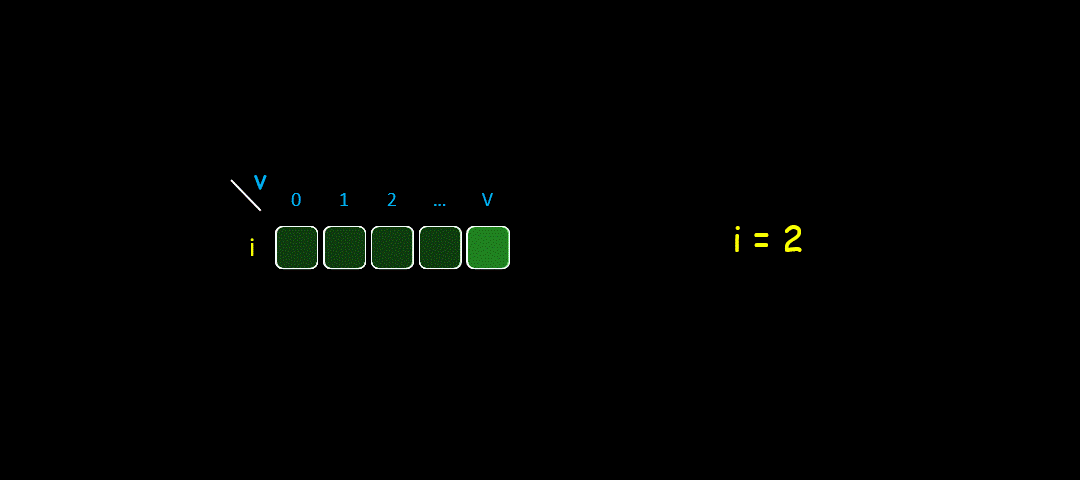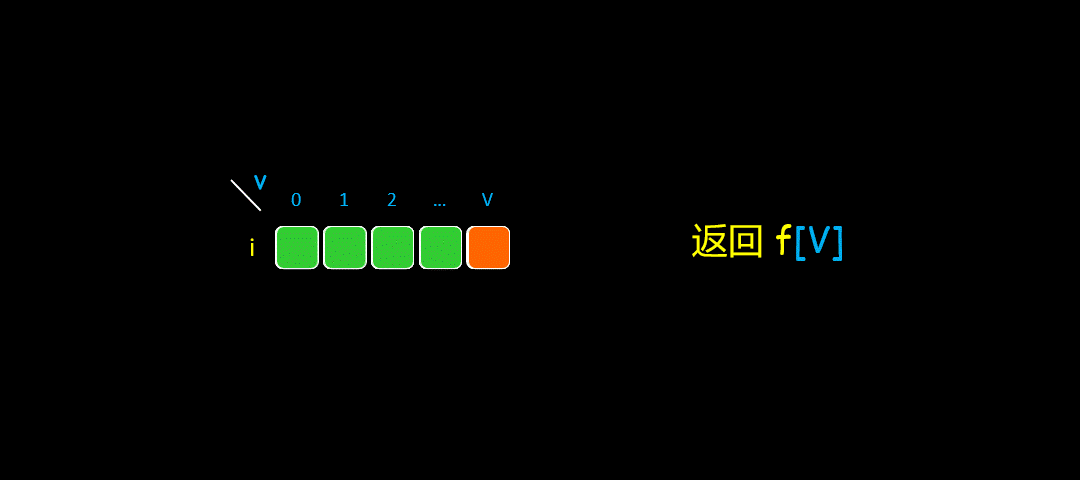
在二维数组中，每一行的数据都是由上一行得到的，我们把它变成一维数组，二维数组的上一行数据就是它当前状态。

转载自：
经典动态规划：0-1 背包问题
leetcode题解