大数据分析与应用：探索聚类分析的奥秘_8.聚类分析是在给定训练集的基础上,构建分类模型(即分类器),把未知数据(-CSDN博客

本文链接：https://blog.csdn.net/QovJ_00K208/article/details/143380592

一、聚类分析的基本原理

二、聚类算法的分类

在当今信息化时代，数据无处不在，大数据分析成为各行各业挖掘潜在价值、优化决策的重要手段。聚类分析作为数据挖掘中的一种关键技术，通过将数据集中的对象分组，使得同一组内的对象具有较高的相似性，而不同组之间的对象则相似性较低。本文将深入探讨聚类分析的基本原理、核心算法以及实际应用，并附上运行代码和经典数据示例，以期为读者提供一个全面而实用的学习指南。

一、聚类分析的基本原理

聚类分析是一种无监督学习方法，其核心思想是通过相似性度量标准，将数据集中的对象划分为若干个子集（即簇），使得同一簇内的对象相似度高，而不同簇之间的对象相似度低。这里的对象可以是数值、文本、图像等多种数据类型，相似性度量则常用欧氏距离、曼哈顿距离、余弦相似度等标准。

二、聚类算法的分类

三、核心算法及其操作步骤

1. K-Means聚类算法

K-Means是一种简单且广泛应用的聚类算法，它将数据集划分为K个簇，其中K是用户预先指定的正整数。算法的具体操作步骤如下：

初始化：随机选择K个数据点作为初始质心。
分配：对于数据集中的每一个数据点，计算它到各个质心的距离，并将其分配给最近的那个质心所在的簇。
更新：对于每一个簇，重新计算其质心，通常是取该簇内所有点的平均值。

迭代：重复执行分配和更新步骤，直到满足某个停止条件，如质心不再变化或达到最大迭代次数。

import numpy as np  
import matplotlib.pyplot as plt  
from sklearn.cluster import KMeans  
from sklearn.datasets import make_blobs  
  
# 生成样本数据  
n_samples = 300  
random_state = 42  
X, y = make_blobs(n_samples=n_samples, centers=4, random_state=random_state)  
  
# 创建KMeans实例并拟合数据  
kmeans = KMeans(n_clusters=4, random_state=random_state)  
kmeans.fit(X)  
  
# 预测每个样本所属的簇  
labels = kmeans.labels_  
  
# 获取质心  
centroids = kmeans.cluster_centers_  
  
# 可视化结果  
plt.figure(figsize=(8, 6))  
colors = ['r', 'g', 'b', 'y']  # 定义四种颜色表示四个簇  
for i in range(4):  # 绘制属于同一簇的数据点  
    points = X[labels == i]  
    plt.scatter(points[:, 0], points[:, 1], s=50, c=colors[i], label=f'Cluster {i+1}')  
  
# 绘制质心  
plt.scatter(centroids[:, 0], centroids[:, 1], s=200, c='black', marker='X', label='Centroids')  
  
# 添加图例和标题  
plt.legend()  
plt.title('K-Means Clustering')  
plt.show()

运行为：

上述代码使用make_blobs函数生成了一个包含300个样本点的数据集，分为4个中心。通过KMeans类创建了一个K-Means模型，并指定要形成的簇的数量为4。最后，利用Matplotlib绘制出数据点及它们对应的簇中心。

2. K-medoids聚类算法

其原理与K-Means算法相似，但关键区别在于它使用数据集中的实际点（称为medoids）作为簇的中心点，而不是像K-Means那样使用簇内所有点的平均值。与K-Means算法相比，K-medoids算法的计算复杂度更高，因为每次迭代都需要在每个簇中选择一个新的medoid，这通常涉及大量的距离计算。K-medoids算法的性能也受到初始medoids选择的影响，不同的初始选择可能导致不同的聚类结果。

3.K-prototype聚类算法

K-medoids算法通过迭代的方式，从数据集中选择K个数据点作为medoids（中心点或代表点），然后将其余数据点分配到离它们最近的medoid所属的簇中。与K-means算法不同的是，K-medoids算法选择的medoids必须是数据集中的实际点，而不是簇内所有点的平均值。

4. BIRCH聚类算法

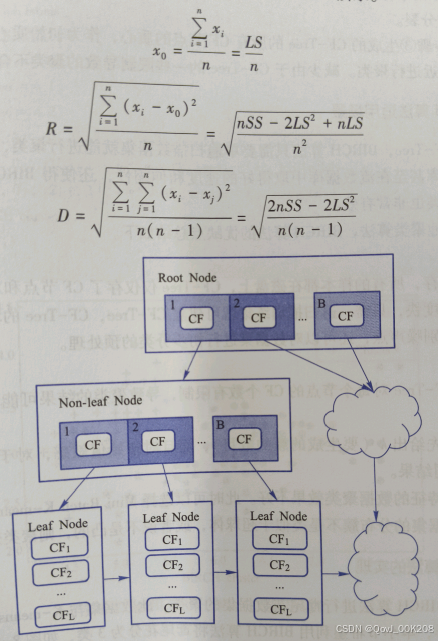
BIRCHBalanced Iterative Reducing and Clustering using Hierarchies）是一种特别适用于大型数据集的聚类算法。它通过构建层次结构的聚类特征树（CF Tree）来有效处理大量数据，并支持动态地调整聚类的数量。

主要特点：

能够在有限的内存中处理大量数据。
只需一次遍历整个数据集即可构建CF树。
支持动态地调整聚类的数量。

from sklearn.cluster import Birch
from sklearn import metrics
y_pred = Birch(n_clusters=None).fit_predict(X)
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.show()
#Calinski-Harabasz指数（也称为variance ratio criterion）衡量聚类间的差异与聚类内差异的比
print("Calinski-Harabasz Score", metrics.calinski_harabasz_score(X, y_pred))

请注意，BIRCH算法的实际应用中可能需要根据具体问题调整参数，如threshold和branching_factor，以及进行适当的数据预处理。

5.CURE聚类算法

CURE（Clustering Using Representatives）算法是一种可伸缩的层次聚类算法，特别适用于处理大型数据集、离群点和非球形簇。

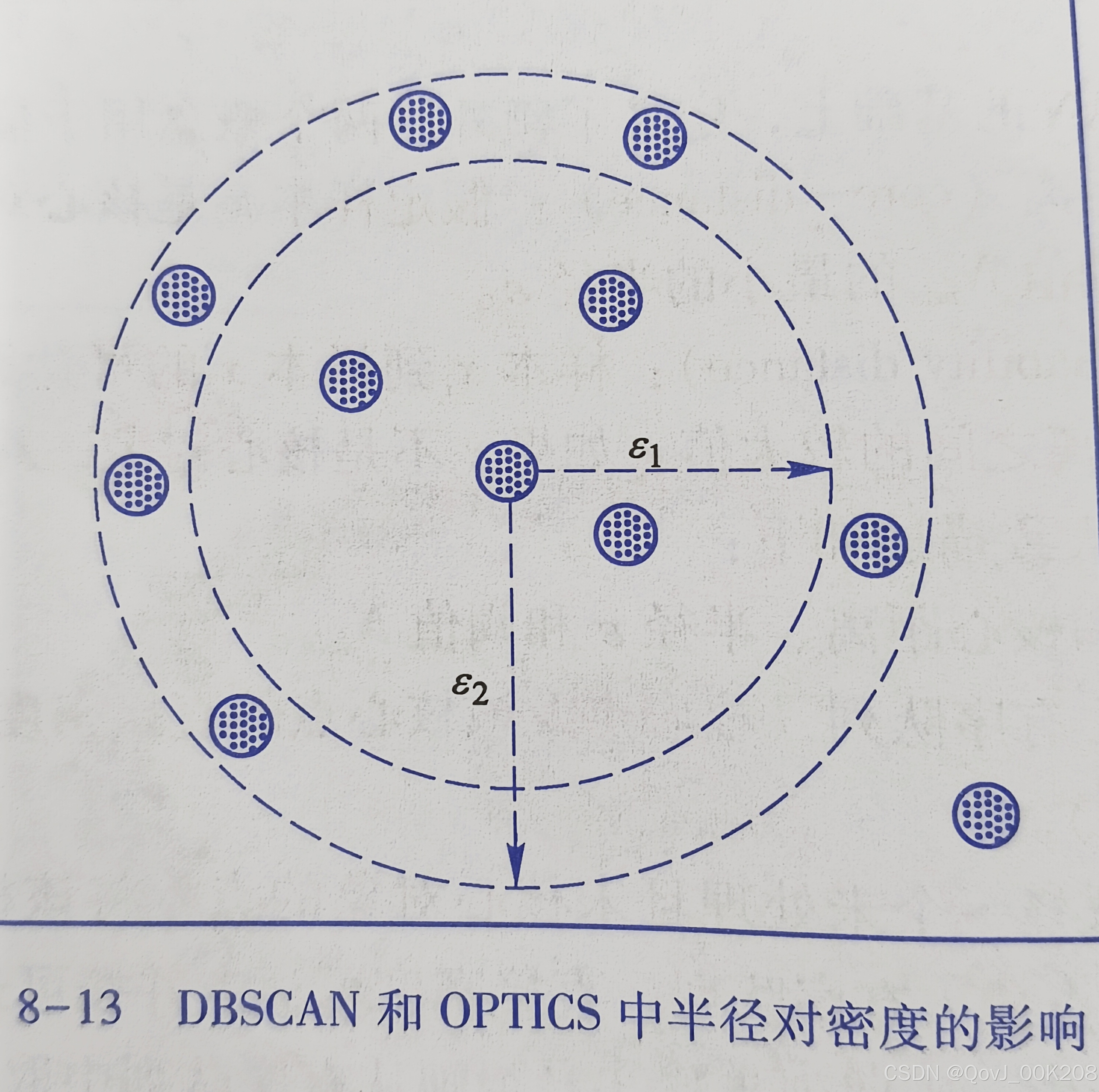
6.DBSCAN聚类算法

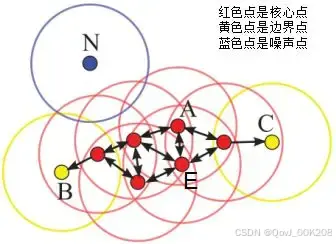
DBSCAN是基于密度空间的聚类算法，在机器学习和数据挖掘领域有广泛的应用，其聚类原理通俗点讲是每个簇类的密度高于该簇类周围的密度，噪声的密度小于任一簇类的密度。如下图簇类ABC的密度大于周围的密度，噪声的密度低于任一簇类的密度，因此DBSCAN算法也能用于异常点检测。

算法原理：

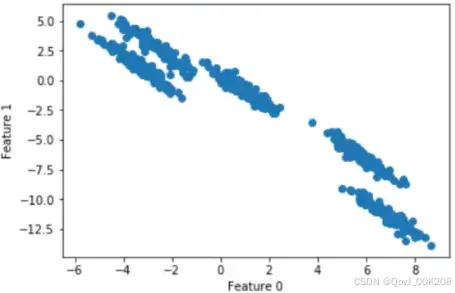
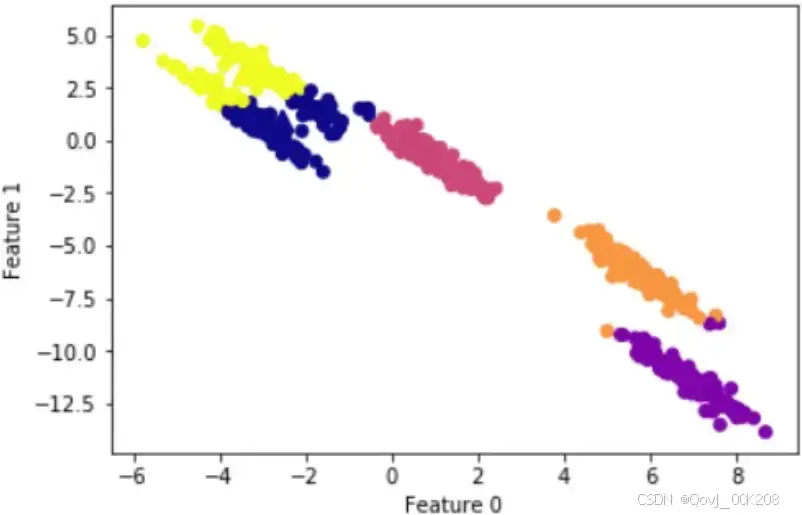
k-means聚类算法假设簇类所有方向是同等重要的，若遇到一些奇怪的形状（如对角线）时，k-means的聚类效果很差。

随机生成五个簇类的二维数据：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import DBSCAN
from sklearn.preprocessing import StandardScaler

# 生成随机簇类数据
X, y =make_blobs(random_state=170,n_samples=600,centers=5)
rng = np.random.RandomState(74)
# 数据拉伸
transformation = rng.normal(size=(2,2))
X = np.dot(X,transformation)
# 绘制延伸图
plt.scatter(X[:,0],X[:,1])
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
plt.show()

散点图为：

k-means聚类结果：

7.DENCLUE聚类算法

DENCLUE算法是一种基于密度的聚类算法，其原理主要依赖于对数据点周围局部密度的估计和聚类中心（也称为密度吸引点）的识别。OPTICS算法中虽然对 DBSCAN 算法进行了改进，将参数的影响降低了，但是本质上这两种算法中涉及的密度计算需要通过半径8、阅值N..两个参数，导致密度估计对半径e 非常敏感，研究者为了解决这一问题，引人了统计学的非参数密度估计方法——核密度估计(kemel density estimation)，把每个观测对象都看作周围区域中高概率密度的一个指示器。一个点上的概率密度依赖于从该点到观测对象的距离。基于此，提出了 DENCLUE (DENsity CLUstEring) 算法。在该算法中，使用数学函数来描述每个样本的影响，称之为“影响函数”，通过计算所有样本的影响函数总和，构建样本空间的整体密度，即全局密度函数。在进行聚类时，依据密度吸引点，即全局密度函数的最大值，来实现聚类。

8.STING聚类算法

STING (Statistical Infomation Grid) 算法是一种基于网格的多分辨率的聚类技术，该算法将样本空间区域划分成矩形单元，采用分层和递归方法进行样本空间划分，高层的毎个单元被划分成多个底一层的单元，如图所示。不同层次的矩形单元对应不同的分辨率。每个网格单元的属性的统计信息被作为统计参数预先计算和存储。该算法处理速度很快，其处理时间独立于数据对象的数目，只与量化空间中每一维的单元数有关。

STING聚类层次结构：