十大排序算法
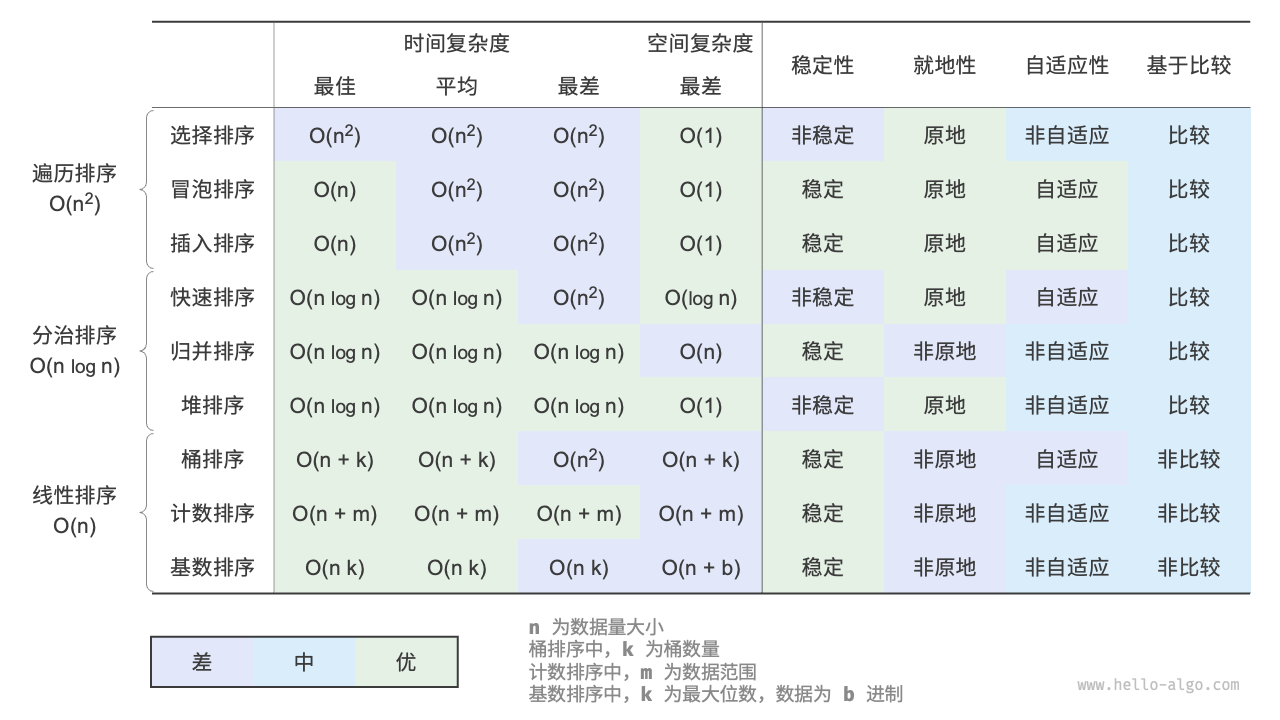
就地性:顾名思义,原地排序通过在原数组上直接操作实现排序,无须借助额外的辅助数组,从而节省内存。通常情况下,原地排序的数据搬运操作较少,运行速度也更快。
稳定性:稳定排序在完成排序后,相等元素在数组中的相对顺序不发生改变。
自适应性:自适应排序的时间复杂度会受输入数据的影响,即最佳时间复杂度、最差时间复杂度、平均时间复杂度并不完全相等。
基于比较的排序算法
常用排序
快速排序
快速排序(Quick Sort)是一种常用的高效的排序算法,它是一种基于比较的排序算法,利用了分治(自顶向下)的思想。快速排序的主要思想是选择一个基准元素,将数组分成两个子数组,一个子数组的所有元素都小于基准元素,另一个子数组的所有元素都大于基准元素,然后递归地对这两个子数组进行排序,最后将它们合并起来。
快速排序的基本步骤如下:
- 选择基准元素:从数组中选择一个元素作为基准(pivot)元素。选择合适的基准元素可以影响算法的性能。
- 划分:将数组中的其他元素与基准元素进行比较,将小于基准元素的元素放在左边,大于基准元素的元素放在右边。最终基准元素将位于其正确的位置,左边是小于它的元素,右边是大于它的元素。
- 递归:递归地对左右两个子数组进行快速排序。
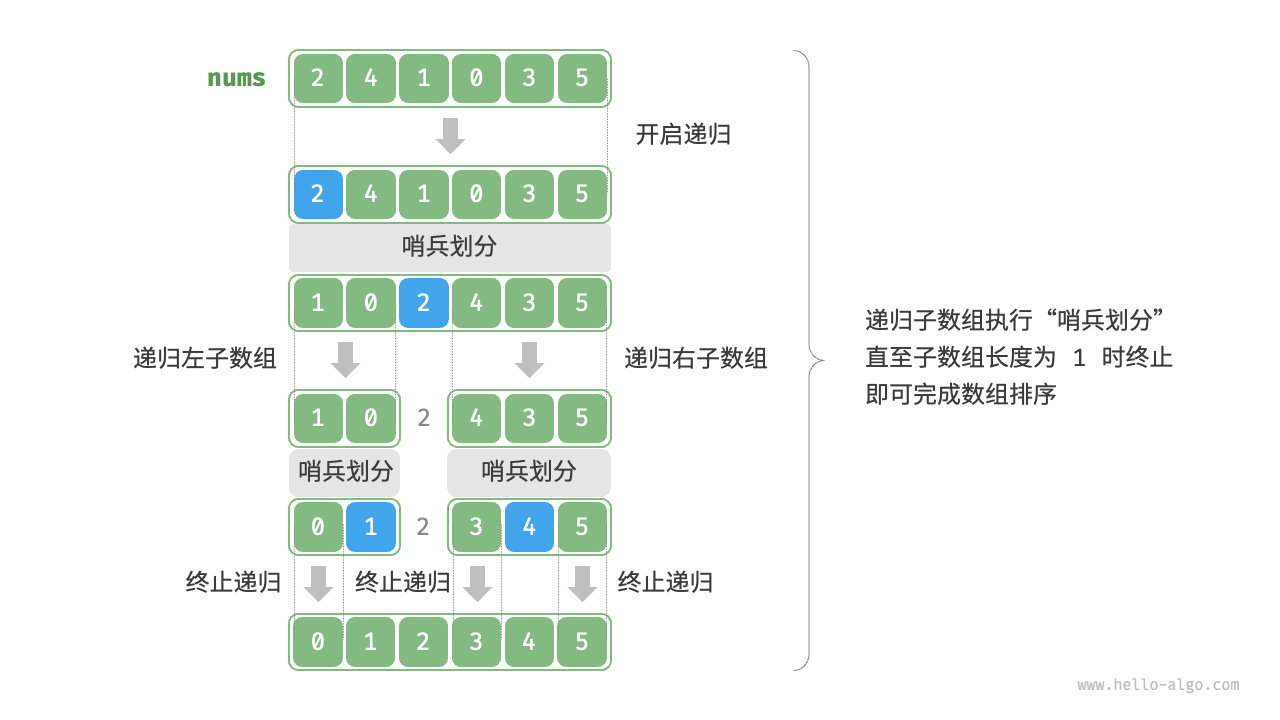
快速排序的平均时间复杂度为O(N * logN),其中N是待排序数组的长度。然而,在最坏情况下,如果选择的基准元素始终是数组中的最小或最大元素,快速排序的时间复杂度可能达到O(N^2),但这种情况相对较少出现。快速排序的实际性能通常比其他基于比较的排序算法好,尤其在大规模数据集上。
优化方案:选择基准元素(随机化(常用),三数取中法),双指针(三向划分)快速排序,小规模子数据使用插入排序。
在快速排序中,如果每次选择基准元素都是数组中的最小或最大元素,那么每次分割都会将数组分成一个元素和 N - 1 个元素的子数组,导致算法的时间复杂度退化为 O(N^2)。随机选择基准元素可以降低这种最坏情况发生的概率,从而避免退化。
import java.util.Random;
/**
* 随机化基准元素优化快速排序
*/
public class QuickSort {
private Random random = new Random();
public int[] sortArray(int[] nums) {
if (nums == null || nums.length < 2) {
return nums;
}
quickSort(nums, 0, nums.length - 1);
return nums;
}
private void quickSort(int[] nums, int low, int high) {
// 边界情况
if (low >= high) {
return;
}
// 自上而下递归根据基准元素进行划分子数组
int pivot = partition(nums, low, high);
quickSort(nums, low, pivot - 1);
quickSort(nums, pivot + 1, high);
}
private int partition(int[] nums, int low, int high) {
// 随机化基准元素,避免基本有序情况下的不平衡划分,将基准元素移到当前子数组的起始位置
int randomIndex = low + random.nextInt( high - low + 1);
int pivot = nums[randomIndex];
nums[randomIndex] = nums[low];
nums[low] = pivot;
// 双指针遍历后,数组基准元素位置左边小于基准元素,右边大于基准元素
while (low < high) {
while (low < high && nums[high] > pivot) {
high--;
}
nums[low] = nums[high];
while (low < high && nums[low] < pivot) {
low++;
}
nums[high] = nums[low];
}
nums[low] = pivot;
return low;
}
}通常快速排序的效率更高,主要有以下原因:
- 出现最差情况的概率很低:虽然快速排序的最差时间复杂度为 O(N^2),没有归并排序稳定,但在绝大多数情况下,快速排序能在 O(N * logN) 的时间复杂度下运行。
- 缓存使用效率高:在执行哨兵划分操作时,系统可将整个子数组加载到缓存,因此访问元素的效率较高。而像“堆排序”这类算法需要跳跃式访问元素,从而缺乏这一特性。
归并排序
归并排序(Merge Sort)是一种基于分治(自底向上)的排序算法,它的主要思想是将一个未排序的数组划分为两个子数组,分别对这两个子数组进行排序,然后再将排好序的子数组合并成一个有序数组。归并排序的关键步骤在于"合并"操作,这是通过将两个已排序的子数组按照顺序合并而实现的。
归并排序的过程可以分为以下几个步骤:
- 分解:将待排序的数组分成两个子数组,通常是将数组分成相等大小的两部分,直到每个子数组的大小为1或0为止,因为一个元素的数组是有序的。
- 排序:对每个子数组进行递归地排序。这个步骤通过将问题逐步分解为更小的子问题,直到达到基本情况(即单个元素的数组),然后逐步合并子问题的解来实现排序。
- 合并:将已排序的子数组合并为一个有序数组。这是归并排序的核心步骤,它通过比较两个子数组中的元素,并按照顺序将它们合并到一个新的数组中,直到所有元素都被合并。
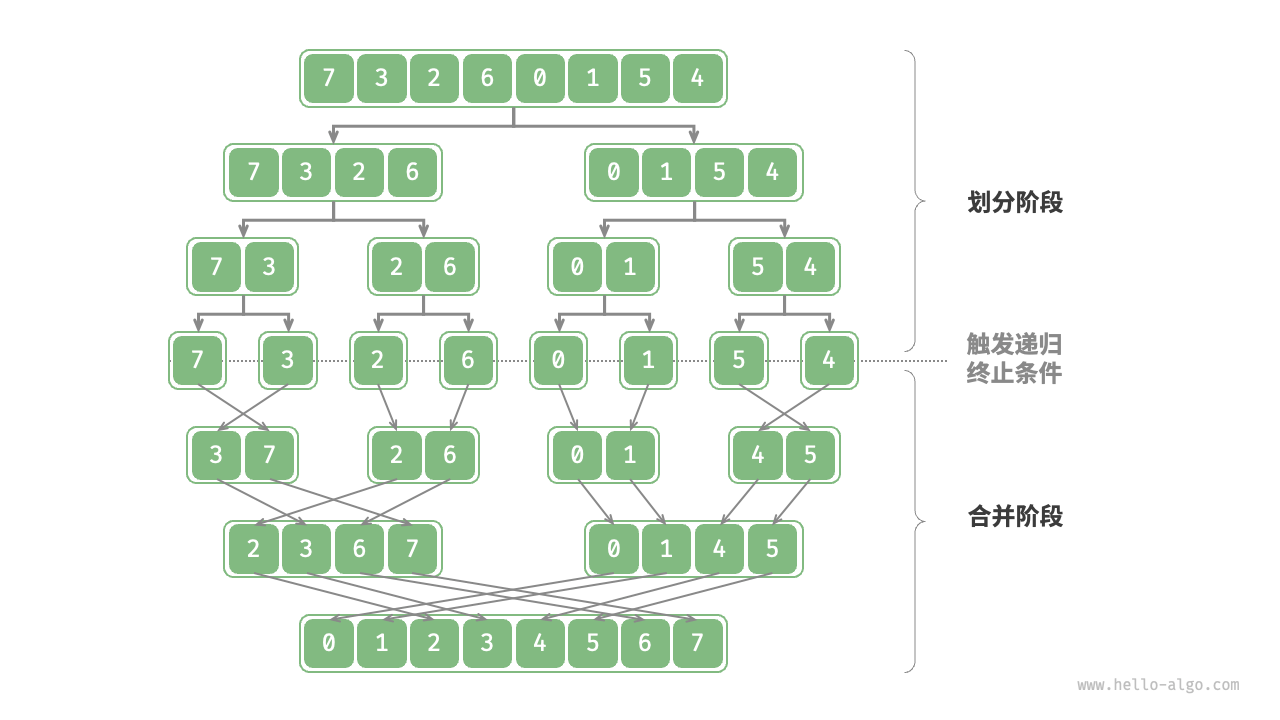
归并排序具有稳定性,即相等元素的顺序在排序后仍然保持不变。其时间复杂度为O(N * logN),其中N是数组的大小,这使得归并排序在大规模数据集上表现出色。然而,它需要额外的空间来存储临时数组,所以空间复杂度为O(N)。
/**
* 归并排序
*/
public class MergeSort {
public int[] sortArray(int[] nums) {
if (nums == null || nums.length < 2) {
return nums;
}
mergeSort(nums, 0, nums.length - 1);
return nums;
}
private void mergeSort(int[] nums, int left, int right) {
// 边界情况
if (left >= right) {
return;
}
int mid = left + (right - left) / 2;
// 自上而下分治
mergeSort(nums, left, mid);
mergeSort(nums, mid + 1, right);
// 自下而上合并
mergeArray(nums, left, mid, right);
}
private void mergeArray(int[] nums, int left, int mid, int right) {
int[] helperArray = new int[right - left + 1];
int leftPointer = left;
int rightPointer = mid + 1;
int i = 0; // 辅助数组索引
while (leftPointer <= mid && rightPointer <= right) {
helperArray[i++] = nums[leftPointer] < nums[rightPointer] ?
nums[leftPointer++] : nums[rightPointer++];
}
while (leftPointer <= mid) {
helperArray[i++] = nums[leftPointer++];
}
while (rightPointer <= right) {
helperArray[i++] = nums[rightPointer++];
}
for (i = 0; i < helperArray.length; i++) {
nums[left + i] = helperArray[i];
}
}
}堆排序
堆排序(Heap Sort)是一种基于二叉堆数据结构的排序算法,它是一种选择排序的一种改进,具有较好的时间和空间复杂度。堆是一种特殊的完全二叉树,分为最大堆和最小堆两种类型,其中最大堆要求父节点的值大于或等于子节点的值,最小堆要求父节点的值小于或等于子节点的值。
堆排序的基本思想:首先将待排序的数组构建成一个二叉堆(通常使用最大堆),出元素的时候将堆顶元素(即最大元素)与堆的最后一个元素交换,并从堆中移除,然后对剩余的元素重新调整为一个合法的堆,重复这个过程直到堆为空,得到一个有序的数组。
以下是堆排序的关键步骤:
- 构建最大堆:从最后一个非叶子节点开始,自底向上地将数组调整为一个最大堆(构建最大堆的时间复杂度是 O(N))。
- 交换堆顶元素和末尾元素:将堆顶元素与堆的最后一个元素交换,然后将堆的大小减一。
- 调整堆:从堆顶开始,通过逐级下沉(或上浮)操作将堆重新调整为最大堆。(调整堆的时间复杂度是O(logN))
- 重复步骤 2 和 3,直到堆为空。
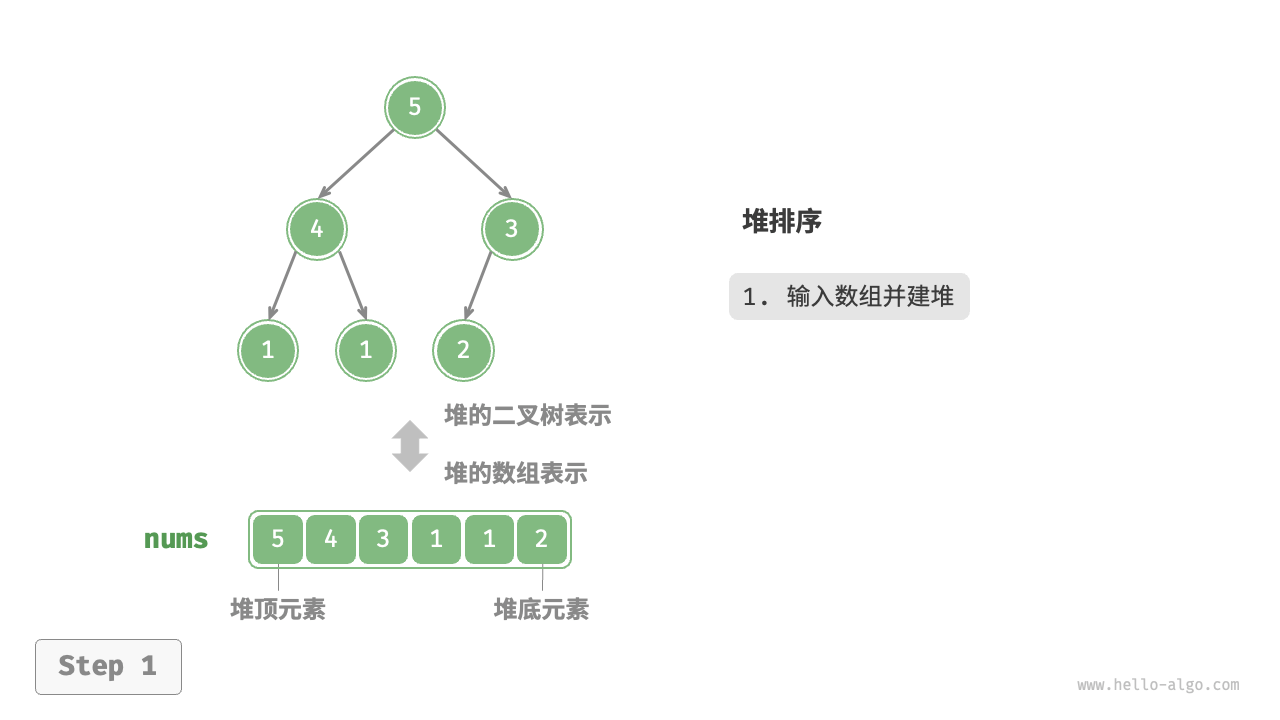
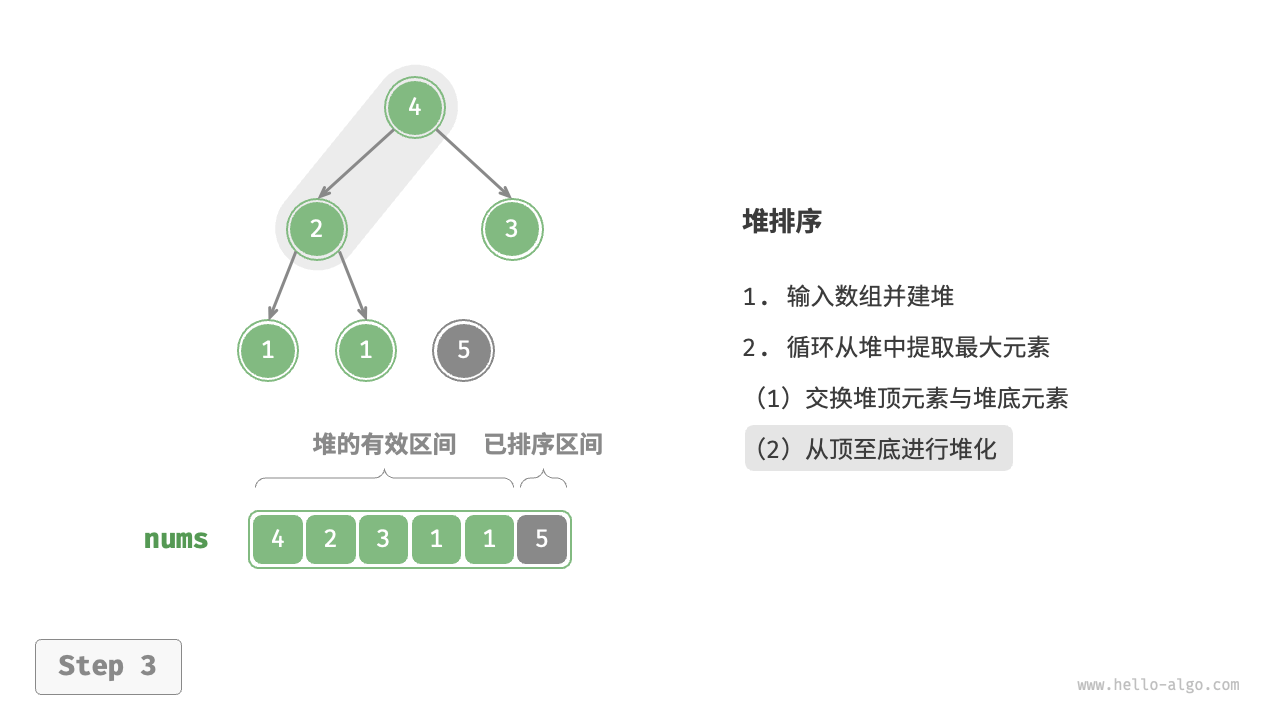
Poor use of cache memory:平均时间上,堆排序的时间常数比快排要大一些,因此通常会慢一些,但是堆排序最差时间也是O(N * logN),这点比快排好。快排在递归进行部分的排序的时候,只会访问局部的数据,因此缓存能够更大概率的命中;而堆排序的建堆过程是整个数组各个位置都访问到的,后面则是所有未排序数据各个位置都可能访问到的,所以不利于缓存发挥作用。简单的说就是快排的存取模型的局部性更强,堆排序差一些。
/**
* 堆排序
* 非叶子节点:在完全二叉树中,所有非叶子节点的索引都在 0 到 n / 2 - 1 之间,其中 n 是数组的长度。
* 叶子节点:叶子节点是树的最底层节点,没有子节点。在完全二叉树中,从 n / 2 到 n - 1 的节点都是叶子节点。
*/
public class HeapSort {
public int[] sortArray(int[] nums) {
if (nums == null || nums.length < 2) {
return nums;
}
int n = nums.length;
// 从最后一个非叶子节点自下而上进行调整
for (int i = n / 2 - 1; i >= 0; i--) {
heapify(nums, n, i);
}
for (int i = n - 1; i >= 0; i--) {
swap(nums, 0, i);
heapify(nums, i, 0);
}
return nums;
}
/**
* 堆化方法,维护堆的性质
* @param nums 数组表示的堆
* @param n 堆的大小
* @param i 当前需要堆化的节点的索引
*/
private void heapify(int[] nums, int n, int i) {
int largest = i;
int left = 2 * i + 1; // 左子节点的索引
int right = 2 * i + 2; // 右子节点的索引
if (left < n && nums[left] > nums[largest]) {
largest = left;
}
if (right < n && nums[right] > nums[largest]) {
largest = right;
}
if (largest != i) {
swap(nums, largest, i);
heapify(nums, n, largest);
}
}
private void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}低级排序
冒泡排序
public class BubbleSort {
// 冒泡排序
public void bubbleSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
for (int i = arr.length - 1; i > 0; i--) {
for (int j = 0; j < i; j++) {
if (arr[j] > arr[j + 1]) {
swap(arr, j, j + 1);
}
}
}
}
}我们发现,如果某轮“冒泡”中没有执行任何交换操作,说明数组已经完成排序,可直接返回结果。因此,可以增加一个标志位 flag 来监测这种情况,一旦出现就立即返回。
public class BubbleSort {
public int[] sortArray(int[] nums) {
if (nums == null || nums.length < 2) {
return nums;
}
boolean flag; // 标志该轮循环数组是否已经有序
for (int i = nums.length - 1; i > 0; i--) {
flag = true;
for (int j = 0; j < i; j++) {
if (nums[j] > nums[j + 1]) {
swap(nums, i, j);
flag = false;
}
}
if (flag) {
break;
}
}
return nums;
}
private void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}选择排序
public class SelectionSort {
public void selectionSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
for (int i = 0; i < arr.length - 1; i++) {
int minIndex = i;
// 在未排序部分找到最小值的索引
for (int j = i + 1; j < arr.length; j++) {
minIndex = arr[j] < arr[minIndex] ? j : minIndex;
}
// 将最小值交换到已排序部分的末尾
swap(arr, i, minIndex);
}
}
}直接插入排序
public class InsertionSort {
// 插入排序,比较有效地排序方法
public void insertionSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
for (int i = 1; i < arr.length; i++) {
// [0, i) 范围内有序,这里的 i 是要比较的元素位置
for (int j = i - 1; j >= 0 && arr[j] > arr[j + 1]; j--) {
swap(arr, j, j + 1);
}
}
}
}尽管插入排序的时间复杂度更高,但在数据量较小的情况下,插入排序通常更快(递归的栈空间的消耗)。
插入排序在时间复杂度的常数因素上比冒泡排序和选择排序更小:
- 较少的交换操作:插入排序在排序过程中,通常需要较少的交换操作。每次插入一个元素时,只需将其与前面已排序部分进行比较,然后移动这些元素,而不是每次都交换元素的位置。相对于冒泡排序来说,冒泡排序每次比较后都可能进行交换操作,交换操作的次数较多,效率较低。
- 较少的比较操作:插入排序在每次插入时,会逐步将元素插入到正确位置,而不像冒泡,选择排序那样需要反复遍历数组来找到未排序部分的最小元素。
希尔排序
希尔排序(Shell Sort)是一种插入排序的一种改进,它通过将数组分成若干个子序列来进行排序,逐步减小子序列的长度,最终完成排序。希尔排序的核心思想是将间隔较大的元素先排好序,然后逐步减小间隔,直到间隔为1,最后进行一次插入排序。
希尔排序的步骤:
- 选择一个增量序列(也称为间隔序列),常用的增量序列有希尔增量、Hibbard增量和Sedgewick增量等。
- 根据增量序列将数组分成若干个子序列,对每个子序列进行插入排序。
- 逐步减小增量,重复步骤 2,直到增量为1,此时进行一次完整的插入排序,完成排序。
希尔增量序列:最希尔增量是最简单的增量序列,其取值为 N / 2,每次递减一半,直到增量为1。其中,N 是数组的长度。最坏时间复杂度 O(N^2),平均时间复杂度 O(N^1.3)~O(N^1.5)。
Hibbard增量序列:Hibbard增量序列采用 2^k - 1(k 为非负整数)作为增量。Hibbard增量的性能较好,但在实际应用中可能并不总是最优。最坏时间复杂度O(N^3/2),平均时间复杂度O(N^5/4)。
Sedgewick增量序列:Sedgewick增量序列通过 4^k + 3 * 2^(k-1) 和 2^(k+2) * (2^(k+2) - 3) + 1 两种增量交替使用,最坏时间复杂度O(N^(4/3)),平均时间复杂度 O(N^(7/6))。
基于比较的排序算法时间复杂度下限证明
经过k次比较最多能区分的序列个数是2^k,如果有M种序列,需要logM次比较才能区分出大小。那有N个元素的数组有 N! 种排序可能,需要logN!次比较才能区分出大小,使用斯特林公式可知最低复杂度是N * logN。

排序算法会出现不稳定的状态原因
比较操作不考虑相等情况:许多排序算法是基于比较操作的,它们只考虑元素的大小关系,而不考虑相等情况。当两个元素的大小相等时,排序算法可能会交换它们的位置,从而破坏了它们在原始序列中的相对顺序,导致排序结果不稳定。
基于非比较的排序算法
计数排序
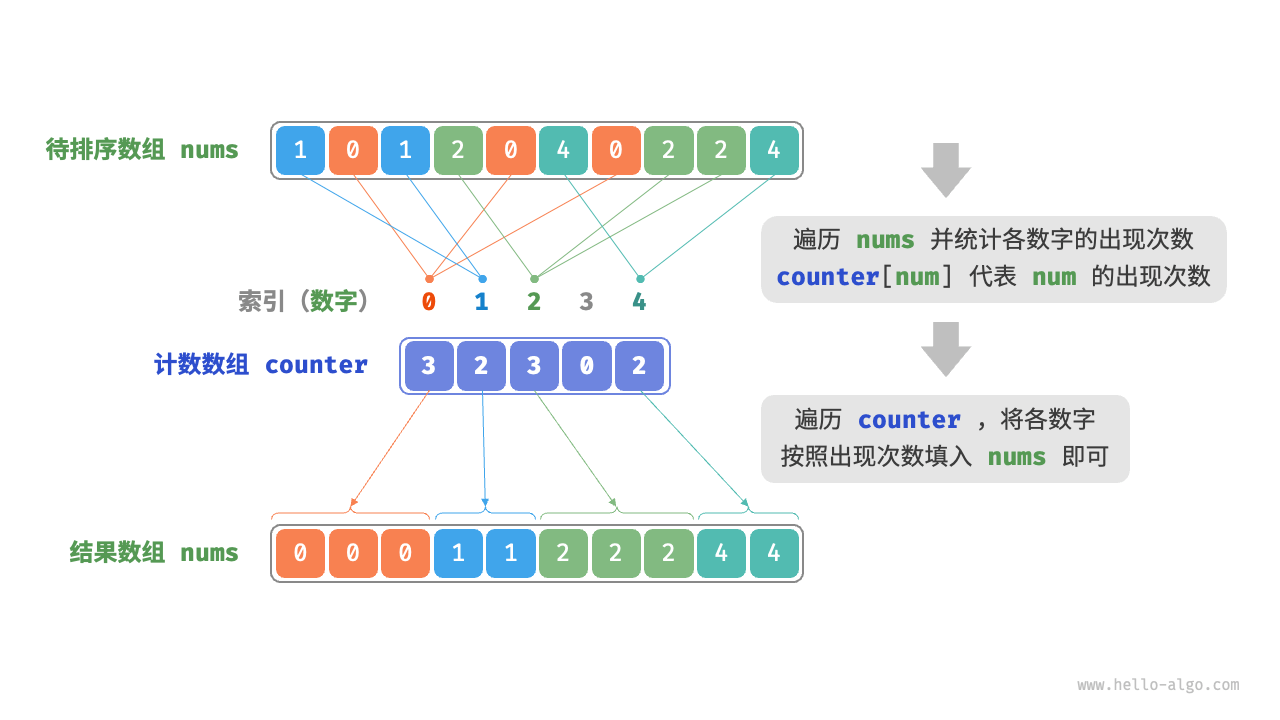
计数排序适用于待排序元素的范围比较小且非负整数的情况。它的基本思想是,统计每个元素出现的次数,然后根据统计信息构建有序的结果序列。
桶排序
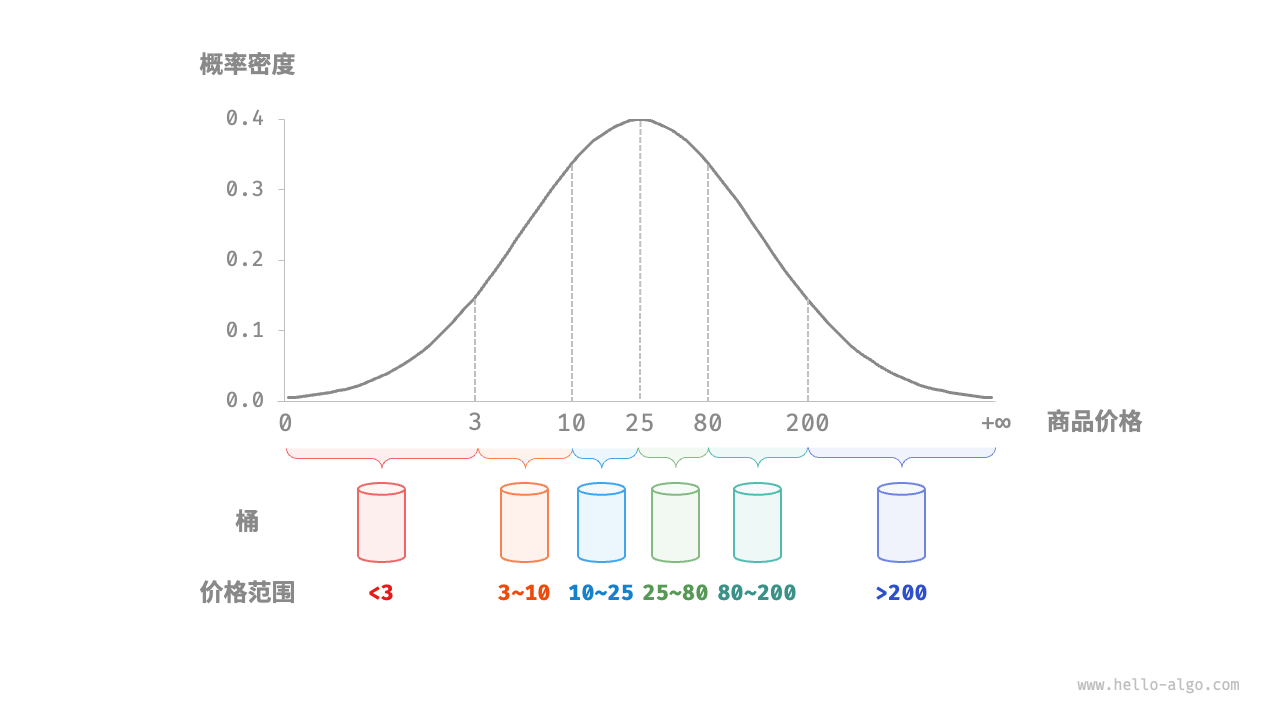
桶排序适用于待排序元素服从均匀分布的情况,它将待排序元素划分为一定数量的桶,然后对每个桶内的元素进行排序,最后将排序后的桶依次合并成有序的结果。
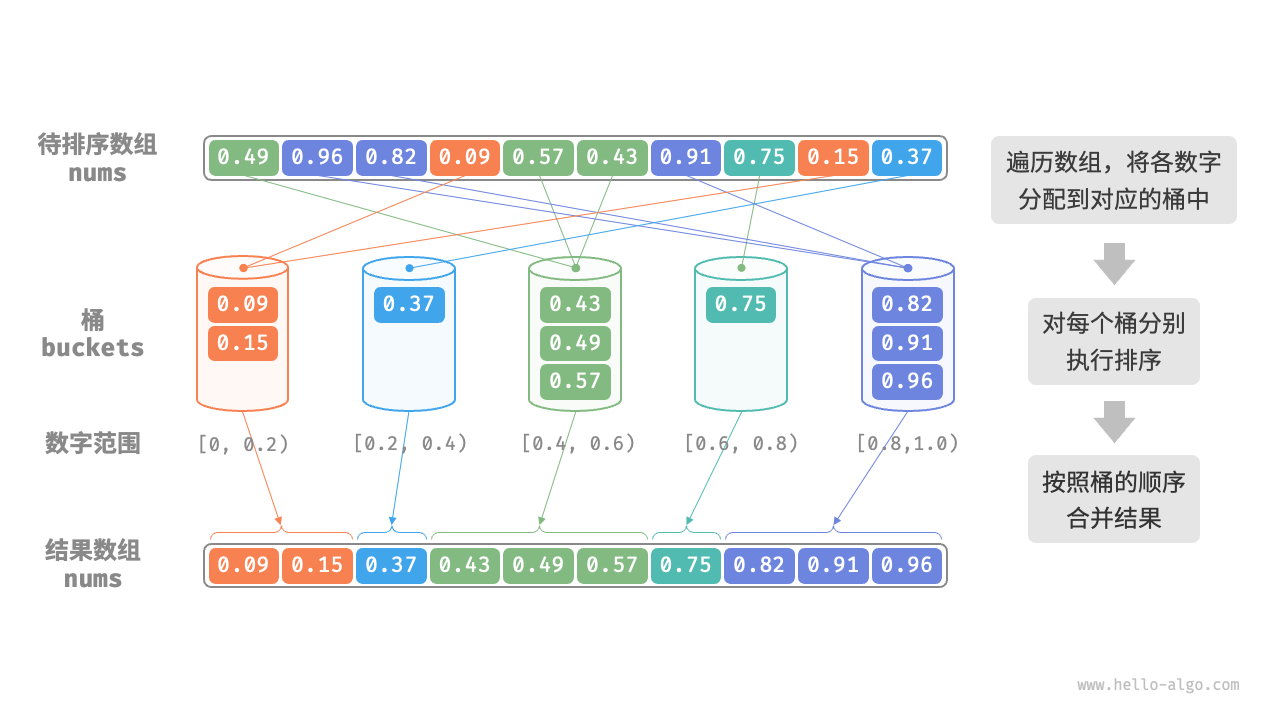
桶排序的时间复杂度理论上可以达到 O(N),关键在于将元素均匀分配到各个桶中,因为实际数据往往不是均匀分布的。为实现平均分配,我们可以先设定一条大致的分界线,将数据粗略地分到 3 个桶中。分配完毕后,再将商品较多的桶继续划分为 3 个桶,直至所有桶中的元素数量大致相等。
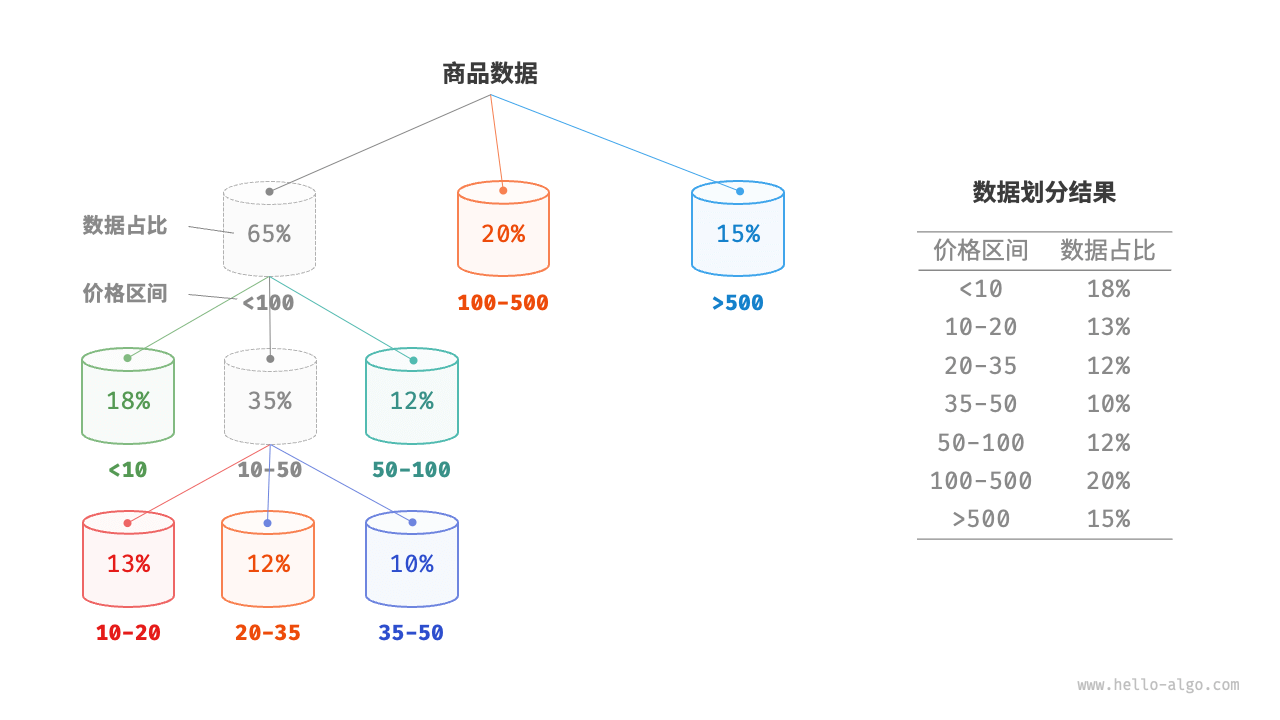
如果我们提前知道商品价格的概率分布,则可以根据数据概率分布设置每个桶的价格分界线。值得注意的是,数据分布并不一定需要特意统计,也可以根据数据特点采用某种概率模型进行近似。
基数排序
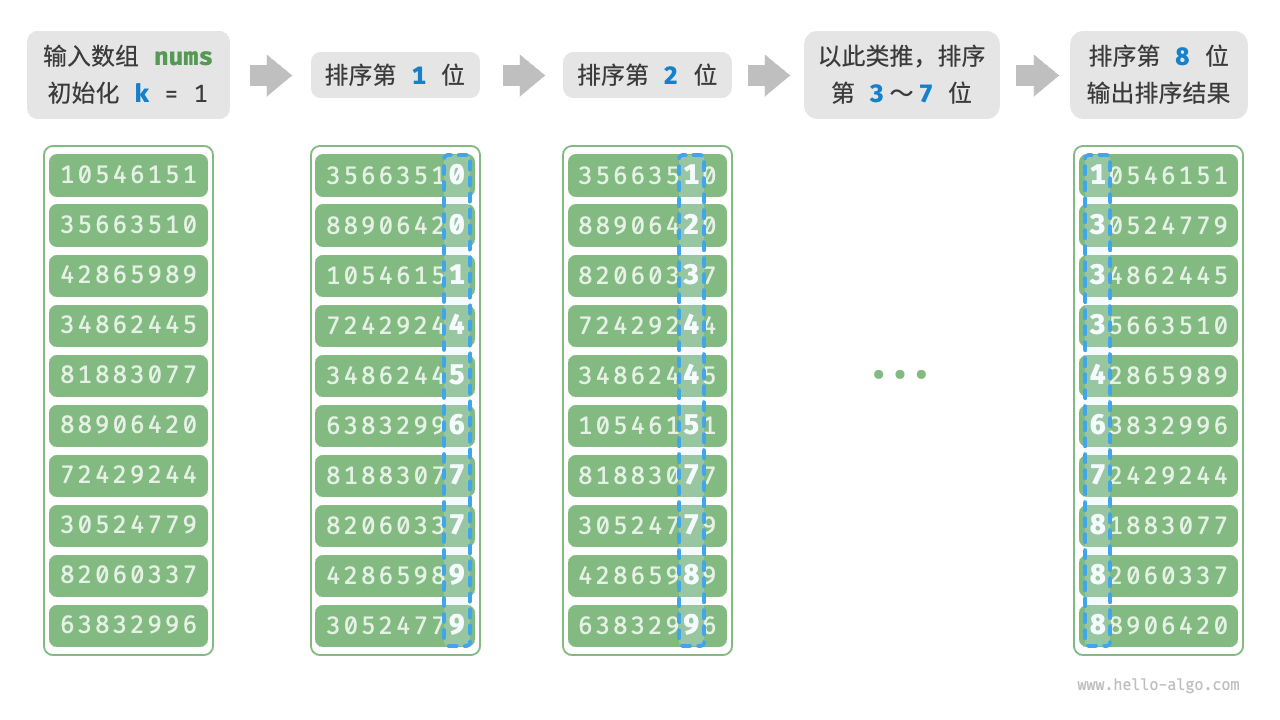
基数排序是一种非比较的排序算法,它适用于整数或字符串等具有固定位数的元素。基数排序的基本思想是将待排序的元素从低位到高位依次进行排序,以实现整体的排序。具体来说,基数排序将元素按照各个位上的值进行桶排序,从最低位到最高位依次进行,最终得到有序的结果。
思考:如何实现在 O(1) 时间复杂度的排序算法?
可以对有限的数字范围内的元素建立一个大哈希表,直接进行映射。
延伸:JDK 中的排序:Arrays.sort 的源码实现
| 数组长度 | 所使用的排序算法 |
| length < 47 | 插入排序 |
| 47 <= length < 286 | 快速排序 |
| length >= 286 且数组基本有序 | 归并排序 |
| length >= 286 且数组基本无序 | 快速排序 |
基本有序的判断方法:逆序对计数法。
延伸:Google 是如何做到如此快的速度对关键词网页进行高质量排序
Google 之所以能够实现如此快速的搜索结果排序,是因为其搜索引擎背后运用了一系列高效的技术和算法。以下是一些关键因素:
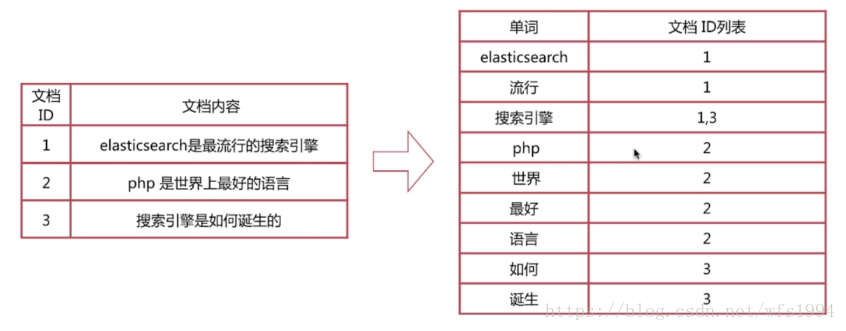
- 索引技术: Google 使用了高度优化的索引技术,例如倒排索引(Inverted Indexing)。这使得系统能够快速定位包含特定关键词的网页,而不需要遍历整个数据集;
- PageRank 算法: Google 的搜索排序算法中,PageRank 算法是一个关键的组成部分。PageRank 基于网页之间的链接关系来评估网页的重要性。这使得搜索结果更加倾向于显示具有高质量内容和受欢迎的网页;
- 分布式计算: Google 的搜索系统是基于大规模的分布式计算架构构建的。这意味着搜索索引和计算是分布在多台服务器上完成的,可以并行处理大量的数据。采用分布式计算可以显著提高搜索速度;
- 机器学习: Google 使用机器学习技术来不断改进搜索排序。通过分析用户的搜索行为、点击模式以及网页的内容,机器学习模型可以自动调整搜索结果的排序,以提供更符合用户需求的结果。
需要注意的是,Google 搜索引擎的高速度是整个系统综合运作的结果,包括硬件、分布式架构、算法优化等多个方面。这种高效性是通过多年来不断的研究和工程实践来实现的。
延伸:外部排序算法
外部排序算法用于处理不能完全装入内存的大型数据集。由于数据量超出了内存容量,需要借助外存(如磁盘)进行排序。外部排序算法的主要思想是将数据分成适当大小的块,逐块排序后再进行合并。以下是外部排序的基本步骤:
分块:假设有一个非常大的数据集,需要对其进行排序,但内存有限。首先,将数据集分成若干个块,每个块的大小应能在内存中完全处理。
- 从数据集中读取一个块的数据到内存中。
- 对该块进行内部排序。
- 将排序后的块写回外存。
- 重复上述步骤,直到所有数据块都已排序并写回外存。
多路归并排序:假设已经有n个排序后的数据块,现在需要将它们合并成一个整体的有序数据集。这一步使用多路归并排序来完成。
- 从每个已排序的块中选取第一个元素,构建一个最小堆。
- 将堆顶元素(最小的元素)输出到最终的有序输出文件中,并从相应的块中读取下一个元素,替换堆顶元素,并调整堆以维持最小堆性质。
- 重复步骤2,直到所有块中的所有元素都已处理完毕。






















 737
737

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








