【C题解题思路】2025华东杯C题解题思路+可运行代码参考（无偿分享）-CSDN博客

本文链接：https://blog.csdn.net/RS_handy/article/details/147647172

注：该内容由“数模加油站”原创，无偿分享，可以领取参考但不要利用该内容倒卖，谢谢！

C 题商品期货涨跌幅预测问题

问题1 数据预处理和特征提取的详细步骤

问题 1 分析

针对商品期货1分钟级主力合约数据的建模，首先需要对原始数据进行系统化的清洗和特征工程处理。由于数据覆盖时间跨度长、合约频繁更替，首先需构建基于品种主力合约的统一视角，确保数据连续性与可比性。其次，考虑到预测任务的本质是基于当前时刻数据预测未来30分钟的涨跌幅，需要构建滚动式窗口样本，将每一分钟的历史走势、成交行为等压缩成窗口特征。在特征构建层面，可以引入多类结构化特征，例如价格统计特征（均值、极差、波动率）、成交量/持仓量变化趋势、技术指标（如MACD、RSI、布林带宽度）等，辅以时间类变量（如分钟数、交易日内相对位置、节假日标记），以捕捉价格微观结构的演化规律。此外，涨跌幅的计算作为标签值必须严格避免数据泄露，即确保30分钟后的价格不会出现在特征提取阶段，所有标签需基于未来数据生成，而特征只能来源于历史窗口。整体的数据处理过程强调时序一致性、信息完整性以及对金融时间序列特有非线性特征的提取能力，为后续建模奠定坚实基础。

解题思路：基于1分钟高频数据的特征提取与涨跌幅标签构建

在商品期货市场中，高频数据（如每分钟K线）蕴含着丰富的市场交易行为信息。为了实现对未来30分钟价格涨跌幅的有效预测，我们首先需对原始的1分钟级主力合约数据进行清洗与结构化预处理，随后通过滑动窗口方式提取高效特征变量，并计算模型预测目标值，即未来30分钟的涨跌幅指标。以下将分步骤详细构建本问题的数学模型。

1. 数据定义与时间标签生成

设原始数据按时间 t 以分钟为间隔给出，记为

预测目标定义为未来30分钟收盘价相对当前价格的变化率，涨跌幅公式如下：

2. 滑动窗口与样本构建机制

为提取能够反映当前市场状态的特征，构造长度为 w 的滑动窗口（如 w=30 或 w=60），在每一时刻 ti 向前提取最近 w 分钟的数据构造一条样本。

窗口样本记为：

3. 时间类特征设计

考虑市场日内效应与开盘/收盘特征，可引入：

当前时间分钟数（如 540 表示第540分钟）；

当前时段类别（如上午交易段/中午停盘/下午交易段）；

当前是否为跳空日（前收盘与当日开盘差距较大）等。

4. 样本构建总结

最终样本构造为：

对应的目标变量：

Python代码：

import os
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler

# 请替换为你的实际文件夹路径
data_folder = r'D:\competition\huadongbei\cta_data\data_'  # 注意：确保路径最后没有多余斜杠

# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 读取部分csv文件（你可根据内存情况调整）
files = sorted([f for f in os.listdir(data_folder) if f.endswith('.csv')])[:10]

# 初始化数据框
all_data = pd.DataFrame()

# 拼接所有数据
for file in files:
    file_path = os.path.join(data_folder, file)
    df = pd.read_csv(file_path)
    df['date'] = file.replace('.csv', '')
    all_data = pd.concat([all_data, df])

# 假设字段名如下，确保这些列存在于CSV中
# 字段：'datetime', 'open', 'high', 'low', 'close', 'volume', 'open_interest'
# 若实际字段不同，请修改下面的字段名
all_data['datetime'] = pd.to_datetime(all_data['datetime'])
all_data.sort_values('datetime', inplace=True)
all_data.reset_index(drop=True, inplace=True)

# 生成未来30分钟涨跌幅标签
all_data['future_close'] = all_data['close'].shift(-30)
all_data['return_30min'] = (all_data['future_close'] - all_data['close']) / all_data['close'] * 100

# 提取滑动窗口特征（以30分钟为窗口）
window = 30
all_data['mean_close'] = all_data['close'].rolling(window).mean()
all_data['std_close'] = all_data['close'].rolling(window).std()
all_data['range_close'] = all_data['close'].rolling(window).apply(lambda x: x.max() - x.min())
all_data['momentum_10'] = all_data['close'] - all_data['close'].shift(10)
all_data['bias_10'] = (all_data['close'] - all_data['close'].rolling(10).mean()) / all_data['close'].rolling(10).mean() * 100

# 删除缺失值
all_data.dropna(inplace=True)

# 标准化选定特征
features = ['mean_close', 'std_close', 'range_close', 'momentum_10', 'bias_10']
scaler = StandardScaler()
all_data[features] = scaler.fit_transform(all_data[features])

# 可视化：收盘价与未来30分钟涨跌幅
plt.figure(figsize=(14, 6))

plt.subplot(1, 2, 1)
plt.plot(all_data['datetime'], all_data['close'], label='Close Price')
plt.title('收盘价走势')
plt.xlabel('时间')
plt.ylabel('价格')
plt.legend()
plt.grid(True)

plt.subplot(1, 2, 2)
plt.plot(all_data['datetime'], all_data['return_30min'], label='30分钟涨跌幅', color='darkorange')
plt.title('未来30分钟涨跌幅')
plt.xlabel('时间')
plt.ylabel('涨跌幅（%）')
plt.legend()
plt.grid(True)

plt.tight_layout()
plt.savefig('收盘价走势_未来30分钟涨跌幅.png')

问题2 模型选择的理由及模型的具体实现

问题 2 分析

本题本质是一个金融时间序列预测任务，预测变量为连续值形式的未来30分钟涨跌幅，因此可视为回归问题中的非平稳、非线性建模任务。在模型选择方面，考虑到原始数据存在时间依赖性、非线性波动和高噪声特点，传统线性回归虽然易于理解，但无法有效建模复杂的价格演化逻辑。基于梯度提升的树模型（如LightGBM或XGBoost）在处理非线性高维特征方面具有较强表现，尤其在中小规模样本下具备高精度和可解释性，适合作为基线模型。若进一步考虑时间序列的动态依赖结构，循环神经网络（如LSTM）和门控单元网络（GRU）可用于构建端到端的预测模型，其优势在于无需显式构造所有历史特征，能够直接从输入序列学习潜在涨跌趋势。此外，若硬件条件允许，基于Transformer结构的时序建模模型（如Informer、Time2Vec-Transformer）在处理长时间跨度、多通道输入数据时也具有较强建模潜力。实际实现中将根据模型类型调整输入维度、窗口长度、标签形式，并结合数据滑动窗口生成机制组织训练数据，以支持高效的并行训练与批量预测。

解题思路：基于回归建模的预测模型选择与实现

本题旨在根据1分钟级别的期货主力合约数据，预测未来30分钟的价格涨跌幅。根据第一问中所定义的标签变量：

该问题属于典型的连续型目标回归预测问题，但由于数据来自高频金融市场，涨跌幅的变化不仅受到当前价格和成交量等量化变量影响，还可能存在强烈的非线性关系和时间序列依赖性。因此，模型的选择应当从拟合能力、泛化能力和可解释性等多方面综合考虑。

一、基线模型：线性回归与岭回归

我们首先考虑传统的线性回归模型：

以 LightGBM 为例，其特点包括：

采用基于直方的叶子生长策略；

对于高维稀疏特征处理效率高；

训练速度快，支持多线程加速。

该模型对缺失值和变量尺度不敏感，且可以输出特征重要性，从而具备一定可解释性。

三、时序建模模型：LSTM（长短期记忆网络）

若考虑滑动窗口内时间结构，神经网络模型——特别是**长短期记忆网络（LSTM）**非常适合处理具有长期依赖的金融时序数据。

LSTM 能有效捕捉输入特征在时间维度上的动态演化，对具有滞后性、周期性或突变性的金融时间序列具有较强拟合能力。

综合考虑数据量、计算资源与建模目标，建议建模初期以 LightGBM 作为主力模型，并辅以 LSTM 构建时间序列端到端预测模型进行对比实验，从中择优。

Python代码：

import os
import pandas as pd
import numpy as np
import lightgbm as lgb
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error, r2_score

# === 第一步：数据读取与拼接（问题1步骤） ===
data_folder = r'D:\competition\huadongbei\cta_data\data_'  # 修改为你的文件夹路径
files = sorted([f for f in os.listdir(data_folder) if f.endswith('.csv')])[:10]  # 可扩展
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
all_data = pd.DataFrame()

for file in files:
    df = pd.read_csv(os.path.join(data_folder, file))
    df['date'] = file.replace('.csv', '')
    all_data = pd.concat([all_data, df])

# 时间格式处理
all_data['datetime'] = pd.to_datetime(all_data['datetime'])
all_data.sort_values(by='datetime', inplace=True)
all_data.reset_index(drop=True, inplace=True)

# === 第二步：特征构造与标签生成（问题1步骤） ===
all_data['future_close'] = all_data['close'].shift(-30)
all_data['return_30min'] = (all_data['future_close'] - all_data['close']) / all_data['close'] * 100

window = 30
all_data['mean_close'] = all_data['close'].rolling(window).mean()
all_data['std_close'] = all_data['close'].rolling(window).std()
all_data['range_close'] = all_data['close'].rolling(window).apply(lambda x: x.max() - x.min())
all_data['momentum_10'] = all_data['close'] - all_data['close'].shift(10)
all_data['bias_10'] = (all_data['close'] - all_data['close'].rolling(10).mean()) / all_data['close'].rolling(10).mean() * 100

# 去除缺失样本
all_data.dropna(inplace=True)

# 标准化数值特征
features = ['mean_close', 'std_close', 'range_close', 'momentum_10', 'bias_10']
scaler = StandardScaler()
all_data[features] = scaler.fit_transform(all_data[features])

# === 第三步：模型训练与验证 ===
X = all_data[features]
y = all_data['return_30min']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 使用 LightGBM 的 sklearn 风格模型
from lightgbm import LGBMRegressor
from lightgbm.callback import early_stopping, log_evaluation

# 创建模型对象
model = LGBMRegressor(
    objective='regression',
    learning_rate=0.05,
    num_leaves=31,
    feature_fraction=0.9,
    bagging_fraction=0.8,
    bagging_freq=5,
    n_estimators=200,
    random_state=42
)

# 正确方式：用 callbacks 控制 early stopping 和日志输出
model.fit(
    X_train, y_train,
    eval_set=[(X_test, y_test)],
    eval_metric='rmse',
    callbacks=[
        early_stopping(stopping_rounds=20),
        log_evaluation(period=10)  # 每10轮输出一次验证结果
    ]
)

# === 第四步：预测与可视化分析 ===
y_pred = model.predict(X_test)

mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
print(f'MSE: {mse:.4f}, R²: {r2:.4f}')

# 可视化1：预测值 vs 真实值
plt.figure(figsize=(14, 6))

plt.subplot(1, 2, 1)
plt.scatter(y_test, y_pred, alpha=0.3, s=10)
plt.xlabel("真实涨跌幅")
plt.ylabel("预测涨跌幅")
plt.title("预测值 vs 真实值")
plt.grid(True)

# 可视化2：预测误差分布
plt.subplot(1, 2, 2)
errors = y_pred - y_test
plt.hist(errors, bins=50, color='teal', edgecolor='black')
plt.title("预测误差分布")
plt.xlabel("误差")
plt.ylabel("频数")
plt.grid(True)

plt.tight_layout()
plt.savefig('真实涨跌幅_预测误差分布.png')

问题3 模型训练和验证的过程及结果

问题 3 分析

为了确保模型的泛化能力与预测性能，训练过程需要遵循时间序列建模中的“因果一致性”原则，即训练集中的数据必须早于验证集与测试集的时间点。因此我们采用前滚验证或滑动时间窗策略，将历史样本按时间顺序划分为训练集、验证集与测试集，从而真实模拟未来不可知的预测场景。在模型训练阶段，对于树模型可使用传统的均方误差（MSE）作为优化目标，并引入早停机制避免过拟合；对于神经网络模型，则采用以均方误差或Huber损失函数为核心的回归优化策略，同时结合Adam优化器与学习率衰减策略加速收敛。模型验证过程除使用MSE、MAE和R²等标准回归评价指标外，还应重点关注方向准确率这一金融预测中的关键指标，即预测方向是否与实际涨跌一致。此外，可视化预测值与真实值之间的走势对比曲线、误差残差分布等，也有助于深入理解模型拟合偏差与性能瓶颈。对于参数较多的深度模型，还可引入Dropout、L2正则化等手段以提升其稳健性。

解题思路：模型训练与验证策略设计

针对本题提出的目标变量——未来30分钟的涨跌幅预测（回归任务），我们已选定基于滑动窗口构建的历史统计特征作为模型输入。为了确保预测模型具备真实市场环境下的实用性与可推广性，我们需严格遵循时间序列预测的因果结构，在模型训练与验证过程中避免“未来信息泄露”。因此，合理的样本划分策略、训练机制与评价体系构建将直接决定模型性能优劣。

1. 样本划分：时间序列滑窗+前滚验证法

由于金融时间序列具有时序性与非平稳性，不能简单采用随机划分方式进行训练与验证。我们采用“前滚窗口验证法（Rolling-origin evaluation）”进行训练集和测试集的构造：

该策略既可模拟真实交易时的滚动预测，又能增加验证结果的稳健性。

2. 模型训练策略：正则化与早停机制

以 LightGBM 为例，模型训练过程中应采用正则化手段控制复杂度，如：

3. 性能评估指标：误差型 + 方向型双重评价体系\

本题预测变量为连续型的30分钟涨跌幅，因此我们选取以下两类指标：

（1）误差类指标：

（2）方向准确率指标：

虽然本题是回归预测问题，但其本质服务于涨跌趋势的识别，因此方向预测准确率是关键辅助评价指标：

方向预测准确率（Directional Accuracy）：

4. 模型结果验证：可视化残差分析与时间走势对比

为了更直观地呈现模型预测效果，我们还应结合图形方式进行模型验证，包括但不限于：

真实值 vs 预测值散点图：检验整体拟合程度与偏差结构；

预测误差直方图：反映残差分布形态，观察是否近似正态分布；

Python代码：

import os
import pandas as pd
import numpy as np
import lightgbm as lgb
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# ==== 第一步：读取数据并构造特征与标签 ====
data_folder = r'D:/competition/huadongbei/cta_data/data_'  # 修改为你的本地路径
files = sorted([f for f in os.listdir(data_folder) if f.endswith('.csv')])[:10]

all_data = pd.DataFrame()
for file in files:
    df = pd.read_csv(os.path.join(data_folder, file))
    df['date'] = file.replace('.csv', '')
    all_data = pd.concat([all_data, df])

all_data['datetime'] = pd.to_datetime(all_data['datetime'])
all_data.sort_values(by='datetime', inplace=True)
all_data.reset_index(drop=True, inplace=True)

# 构建标签
all_data['future_close'] = all_data['close'].shift(-30)
all_data['return_30min'] = (all_data['future_close'] - all_data['close']) / all_data['close'] * 100

# 构造滑动窗口特征
window = 30
all_data['mean_close'] = all_data['close'].rolling(window).mean()
all_data['std_close'] = all_data['close'].rolling(window).std()
all_data['range_close'] = all_data['close'].rolling(window).apply(lambda x: x.max() - x.min())
all_data['momentum_10'] = all_data['close'] - all_data['close'].shift(10)
all_data['bias_10'] = (all_data['close'] - all_data['close'].rolling(10).mean()) / all_data['close'].rolling(10).mean() * 100
all_data.dropna(inplace=True)

# 标准化特征
features = ['mean_close', 'std_close', 'range_close', 'momentum_10', 'bias_10']
scaler = StandardScaler()
all_data[features] = scaler.fit_transform(all_data[features])

X = all_data[features]
y = all_data['return_30min']

# ==== 第二步：训练/测试集划分 ====
X_train, X_test, y_train, y_test, dt_train, dt_test = train_test_split(
    X, y, all_data['datetime'], test_size=0.2, shuffle=False  # 时间序列必须保持顺序
)

# ==== 第三步：模型训练 ====
from lightgbm import LGBMRegressor
from lightgbm.callback import early_stopping, log_evaluation

model = LGBMRegressor(
    objective='regression',
    learning_rate=0.05,
    num_leaves=31,
    feature_fraction=0.9,
    bagging_fraction=0.8,
    bagging_freq=5,
    n_estimators=200,
    random_state=42
)

model.fit(
    X_train, y_train,
    eval_set=[(X_test, y_test)],
    eval_metric='rmse',
    callbacks=[early_stopping(20), log_evaluation(10)]
)

# ==== 第四步：结果评估 ====
y_pred = model.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
mae = mean_absolute_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
direction_acc = np.mean(np.sign(y_test) == np.sign(y_pred))

print(f'MSE: {mse:.4f}')
print(f'MAE: {mae:.4f}')
print(f'R²: {r2:.4f}')
print(f'方向预测准确率: {direction_acc:.4f}')

# ==== 第五步：可视化分析 ====
plt.figure(figsize=(15, 12))

# (1) 预测值 vs 真实值 散点图
plt.subplot(2, 2, 1)
plt.scatter(y_test, y_pred, alpha=0.3)
plt.xlabel("真实涨跌幅")
plt.ylabel("预测涨跌幅")
plt.title("预测值 vs 真实值")
plt.grid(True)

# (2) 预测误差分布
plt.subplot(2, 2, 2)
errors = y_pred - y_test
plt.hist(errors, bins=50, color='salmon', edgecolor='black')
plt.title("预测误差分布")
plt.xlabel("误差")
plt.ylabel("频数")
plt.grid(True)

# (3) 时间走势对比
plt.subplot(2, 1, 2)
plt.plot(dt_test.values, y_test, label='真实值', color='blue', linewidth=1)
plt.plot(dt_test.values, y_pred, label='预测值', color='orange', linewidth=1)
plt.xlabel("时间")
plt.ylabel("涨跌幅")
plt.title("预测走势 vs 真实走势")
plt.legend()
plt.grid(True)

plt.tight_layout()
plt.savefig('模型训练验证结果展示.png')

问题4 模型的预测效果分析及改进建议

问题 4 分析

模型预测效果的好坏不仅体现在数值误差指标的优劣上，更体现在对不同市场状态下的适应能力。通过对涨跌幅预测误差进行分布分析，我们可以识别模型是否对高波动时段预测不准，或是否在行情趋稳时出现滞后。此外，分析不同特征在模型中的贡献程度，如通过SHAP值分析（用于Tree模型）或注意力机制热图（用于Transformer模型），可以揭示哪些变量在涨跌预测中起到核心作用，为后续特征工程优化提供依据。对于模型改进方面，可考虑从多个方向着手：一是引入宏观经济变量或跨品种行情关联性特征（如铁矿石价格对螺纹钢的滞后影响），增强模型对外部冲击的感知能力；二是探索多模型集成策略，例如Blending或Stacking方式融合轻量模型与深度模型，以提升预测稳健性；三是将当前模型结果引入到模拟交易系统中，通过策略回测评估预测价值的实际收益能力，为模型选择提供收益导向的反馈机制。最终通过系统性的误差分析与迭代优化，形成一套能够兼顾精度、泛化性与应用价值的商品期货预测模型框架。

解题思路：模型预测效果分析与改进建议

在完成特征构建与模型训练后，为了检验所建模型在实际金融预测任务中的适用性，我们需对预测结果进行多角度的系统性评估与可视化分析，重点关注模型在方向判断、涨跌幅度控制、误差分布结构等方面的表现。此外，为提升模型性能与稳健性，有必要对现有模型进行局限性剖析，并从特征增强、模型融合与目标重定义等方向提出优化建议。

一、误差结构分析与度量指标构建

二、涨跌方向判断能力评估

在期货交易中，预测方向的准确性往往比精确的数值回归更具实用价值。因此我们定义方向预测准确率：

方向一致性率（Direction Accuracy, DA）：

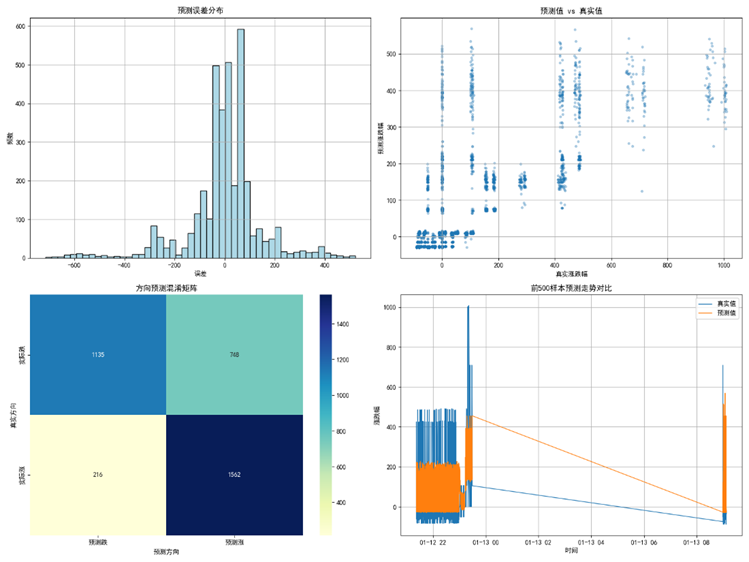
此外，可以进一步绘制混淆矩阵，区分“预测涨却下跌”、“预测跌却上涨”等类型误判，对交易系统具有直接意义。

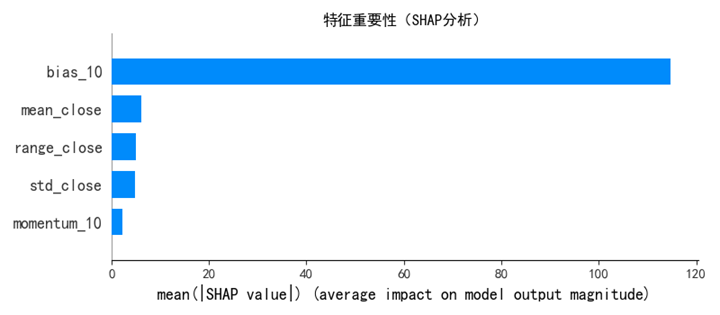
三、特征贡献度与模型可解释性分析

为探讨模型对不同输入特征的依赖程度，可对以 LightGBM 或 XGBoost 为代表的树模型计算特征重要性，主要方式有：

基于分裂增益（Gain）：

特征重要性分析可帮助识别无效或噪声特征，便于下一轮模型精简与重构。

四、模型不足与性能瓶颈分析

结合第三问中的可视化与指标结果，模型仍可能存在以下典型局限：

方向误判较多：对临界波动方向判断不稳定；

误差分布偏斜：在极端涨跌行情中预测失效；

特征信息丢失：滑动统计量过于粗糙，忽略了高阶结构变化；

序列依赖建模不足：使用静态窗口特征时，未显式建模时序结构，可能忽视惯性或趋势滞后效应。

五、模型优化建议与提升方向

针对上述问题，提出如下多维改进策略：

（1）特征层优化：

引入技术指标类特征如 RSI、MACD、KDJ；

使用高阶统计量（偏度、峰度）捕捉非对称涨跌行为；

引入跨品种特征（如铁矿对螺纹钢联动影响）构建因果推理结构。

（2）模型层改进：

使用 LSTM、Transformer 等序列模型替代滑窗输入；

尝试多模型集成策略（如 Blending、Stacking）提升稳健性；

构建分类辅助模型预测方向，同时叠加回归预测涨幅大小，形成“两阶段模型”。

（3）目标函数重构：

考虑自定义加权损失函数，对预测方向错误的样本惩罚更大，定义为：

Python代码：

import os
import pandas as pd
import numpy as np
import lightgbm as lgb
import shap
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score, confusion_matrix
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# === 1. 数据加载与特征工程 ===
data_folder = r'D:/competition/huadongbei/cta_data/data_'  # 修改为你的数据路径
files = sorted([f for f in os.listdir(data_folder) if f.endswith('.csv')])[:10]

all_data = pd.DataFrame()
for file in files:
    df = pd.read_csv(os.path.join(data_folder, file))
    df['date'] = file.replace('.csv', '')
    all_data = pd.concat([all_data, df])

all_data['datetime'] = pd.to_datetime(all_data['datetime'])
all_data.sort_values(by='datetime', inplace=True)
all_data.reset_index(drop=True, inplace=True)

# 标签生成
all_data['future_close'] = all_data['close'].shift(-30)
all_data['return_30min'] = (all_data['future_close'] - all_data['close']) / all_data['close'] * 100

# 特征生成
window = 30
all_data['mean_close'] = all_data['close'].rolling(window).mean()
all_data['std_close'] = all_data['close'].rolling(window).std()
all_data['range_close'] = all_data['close'].rolling(window).apply(lambda x: x.max() - x.min())
all_data['momentum_10'] = all_data['close'] - all_data['close'].shift(10)
all_data['bias_10'] = (all_data['close'] - all_data['close'].rolling(10).mean()) / all_data['close'].rolling(10).mean() * 100
all_data.dropna(inplace=True)

# 特征标准化
features = ['mean_close', 'std_close', 'range_close', 'momentum_10', 'bias_10']
scaler = StandardScaler()
all_data[features] = scaler.fit_transform(all_data[features])

X = all_data[features]
y = all_data['return_30min']
dt = all_data['datetime']

# === 2. 训练测试集划分 ===
X_train, X_test, y_train, y_test, dt_train, dt_test = train_test_split(
    X, y, dt, test_size=0.2, shuffle=False
)

# === 3. 模型训练 ===
from lightgbm import LGBMRegressor
from lightgbm.callback import early_stopping, log_evaluation

model = LGBMRegressor(
    objective='regression',
    learning_rate=0.05,
    num_leaves=31,
    feature_fraction=0.9,
    bagging_fraction=0.8,
    bagging_freq=5,
    n_estimators=200,
    random_state=42
)

model.fit(
    X_train, y_train,
    eval_set=[(X_test, y_test)],
    eval_metric='rmse',
    callbacks=[early_stopping(20), log_evaluation(10)]
)

# === 4. 性能评估 ===
y_pred = model.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
mae = mean_absolute_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
direction_acc = np.mean(np.sign(y_test) == np.sign(y_pred))

print(f"MSE: {mse:.4f}")
print(f"MAE: {mae:.4f}")
print(f"R²: {r2:.4f}")
print(f"方向预测准确率: {direction_acc:.4f}")

# === 5. 可视化分析 ===
plt.figure(figsize=(16, 12))

# (1) 残差直方图
plt.subplot(2, 2, 1)
errors = y_pred - y_test
plt.hist(errors, bins=50, color='lightblue', edgecolor='black')
plt.title("预测误差分布")
plt.xlabel("误差")
plt.ylabel("频数")
plt.grid(True)

# (2) 真实 vs 预测
plt.subplot(2, 2, 2)
plt.scatter(y_test, y_pred, alpha=0.3, s=10)
plt.xlabel("真实涨跌幅")
plt.ylabel("预测涨跌幅")
plt.title("预测值 vs 真实值")
plt.grid(True)

# (3) 方向预测混淆矩阵
true_direction = np.where(y_test > 0, 1, 0)
pred_direction = np.where(y_pred > 0, 1, 0)
cm = confusion_matrix(true_direction, pred_direction)
plt.subplot(2, 2, 3)
sns.heatmap(cm, annot=True, fmt='d', cmap='YlGnBu', xticklabels=["预测跌", "预测涨"], yticklabels=["实际跌", "实际涨"])
plt.title("方向预测混淆矩阵")
plt.xlabel("预测方向")
plt.ylabel("真实方向")

# (4) 时间走势预测对比（前500点）
plt.subplot(2, 2, 4)
plt.plot(dt_test.values[:500], y_test.values[:500], label='真实值', linewidth=1)
plt.plot(dt_test.values[:500], y_pred[:500], label='预测值', linewidth=1)
plt.title("前500样本预测走势对比")
plt.xlabel("时间")
plt.ylabel("涨跌幅")
plt.legend()
plt.grid(True)

plt.tight_layout()
plt.savefig("问题4_模型预测效果分析.png")
plt.close()

# === 6. SHAP 特征重要性分析 ===
explainer = shap.Explainer(model)
shap_values = explainer(X_test)

shap.summary_plot(shap_values, X_test, plot_type="bar", show=False)
plt.title("特征重要性（SHAP分析）")
plt.tight_layout()
plt.savefig("问题4_SHAP特征重要性.png")