[时序波动关联]模型CoFLUX论文要点整理

时序波动关联模型CoFLUX论文要点整理

简介

在互联网公司里面，通常都会监控成千上万的时间序列，用于保障整个系统或者平台的稳定性。在这种情况下，如果能够对多条时间序列之间判断其是否相关，则对于监控而言是非常有效的。基于以上的实际情况，清华大学与 Alibaba 集团在2019年一起合作了论文《CoFlux: Robustly Correlating KPIs by Fluctuations for Service Troubleshooting》，并且发表在 IWQos 2019 上。CoFlux 这个方法可以对多条时间序列来做分析，并且主要用途包括以下几点：

1. 告警压缩和收敛；
2. 推荐与已知告警相关的 Top N 的告警；
3. 在已有的业务范围内（例如数据库的实例）构建异常波动传播链；

问题背景

关键术语

KPIs and flux-features（波动特征）
KPI 是在等距时间戳处收集的一系列连续观测值，表示为$S=[s_1,s_2,...,s_m]$，其中s_i是对应于时间索引$i$的观测值，$i\in 1,2,...,m$，$m$是 KPI 的长度。如果两个 KPI 具有不同的采样间隔，在考虑它们的波动相关性时，我们使用它们间隔的最低公倍数作为最终间隔对它们进行重新采样。我们将预测 KPI 定义为由时间序列预测模型产生的一系列预测值，表示为$P=[p_1,p_2,...,p_m]$，其中$p_i$是$s_i$的预测值。预测误差表示为 $F=[f_1,f_2,...,f_m]$，其中 $f_i=s_i-p_i$。虽然可以很好地预测正常观测值，但波动通常会产生预测错误。因此，预测误差在分析波动时非常有用。在这项工作中，预测误差被视为fluctuation features，称为flux-features。因此，用于预测的具有特定参数的时间序列模型是一个特征检测器。我们可以通过不同的时间序列预测模型为 KPI 创建许多flux-features。
图 2 显示了一个真实 KPI 的例子，它通过历史平均值的预测值，得到相应的波动特征。 由于波动特征是由时间序列预测模型生成的，因此模型选择对于波动特征提取至关重要。 如果模型可以准确预测正常值，那么预测误差就可以很好地捕捉波动。

Flux-correlation（波动相关）
在本研究中，对于 KPI 对 X 和 Y，我们首先确定它们的波动是否相关，即波动相关（flux-correlation）。 我们定义：如果 X 和 Y 是波动相关的，表示为$X\sim Y$ 。如果 X 和 Y 不与波动相关，表示为$X\nsim Y$。 例如，图 1 显示了六个 KPI 及其波动特征。 K1 和 K2 的波动特征看起来高度相关，因此它们是波动相关的，即$K_1\sim K_2$。 然而，K1 和 K4 不是波动相关的，即$K_1\nsim K_4$。 当两个 KPI 与波动相关时，我们将继续了解它们的时间顺序以及它们是否在同一方向上波动，如下所述。

输入输出

CoFlux 的输入和输出分别是：
输入：两条时间序列
输出：这两条时间序列的以下信息

1. 波动相关性：两条时间序列是否存在波动相关性？（Q1）
2. 前后顺序：如果两条时间序列相关，那么它们的前后波动顺序是什么？是同时发生异常还是存在固定的前后顺序？（Q2）
3. 方向性：如果两条时间序列是波动相关的，那么它们的波动方向是什么？是一致还是相反？（Q3）

核心思想

为了解决上述问题，我们设计了一种无监督的方法，称为 CoFlux，如图 3 所示。 CoFlux 的输入是两个 KPI。 我们首先通过特征工程提取它们的波动特征，然后测量这些波动特征的相关性。 最后，我们提供问题 Q1∼3 的答案。 需要注意的是，CoFlux 旨在确定长期 KPI 的波动相关性，因此它是一个离线模型，时效性不是我们的目标。 此外，考虑到当前数据，波动相关结果可以定期更新（例如，每周或每月一次）。
特征工程作为该架构的一个关键组成部分，目的在于寻找合适的时间序列模型作为我们的波动特征检测器。 虽然已经提出了许多模型来预测时间序列，例如 MA（移动平均）、TSD（时间序列分解），但每种模型都只能很好地适应时间序列的某些类型的特征。 例如，对于图 1(a) 所示的两个 KPI，K4 具有很强的季节性，而 K5 是稳定的。 对于季节性 KPI，TSD 和历史平均值等模型可能是合适的。 MA 或加权 MA 可以更好地预测稳定的 KPI，因为它们的预测主要依赖于最近的值。 当然，没有通用模型可以准确预测任何类型的 KPI。 如第 1 节所述，挑战在于我们有大量具有不同特征的 KPI。 手动为每个模型搜索合适的预测模型将非常耗时且不切实际。
因此，我们不能依赖单个时间序列模型来提取波动特征。 相反，为了使 CoFlux 尽可能通用，我们采用了几个广为接受的模型，它们具有相应的参数作为波动特征检测器。 这种设计基于以下两个直觉：
● 对于任何给定的 KPI，如果我们广泛调研模型，就会有一个或多个模型能够足够准确地预测其正常观测值并产生接近真实的波动特征。
● 如果X 和Y 这两个KPI 是波动相关的，则X 的至少一个波动特征和Y 的一个波动特征是相关的。
我们使用大量实验来验证这两种直觉。 提取波动特征后，我们继续通过去噪和放大来改进它们。
为了确定波动相关性，对于每对 KPI，我们通过 Crosscorrelation （一种广泛接受的时间序列相似性测量）计算其波动特征的成对相关性。 然后，最大的一个用于确定两个 KPI 是否是波动相关的。 由于我们在 CoFlux 中包含了许多波动特征检测器，其中一些可能能够提取接近真实的波动特征，而另一些可能由于预测不准确而产生误导性的波动特征。 对所有波动特征或多数投票决定进行平均会产生假阴性。 当然，我们只考虑最大值的方法可能会导致潜在的误报。 我们将使用实验来证明使用良好的波动特征检测器，误报非常少。

算法设计

在本节中，我们将详细描述 CoFlux 的两个组件：特征工程和相关性测量。我们从特征工程开始。

特征工程

特征提取

如前所述，KPI 通常具有不同的形状和时间序列特征。为了理解它们的波动相关性，我们需要使用不同的合适的时间序列模型来生成波动特征。我们精心挑选了 7 个广泛使用的模型，如表 1 所示。 Diff只是分别使用最后一天或上周的值来预测当前模型。 Holt-Winters使用三个平滑方程（水平、趋势和季节性分量）计算预测值，其中三个参数的范围从 0 到 1。历史平均值/中值（Historical Average/Median）计算窗口内历史数据的平均值/中值如下一个预测。 TSD（时间序列分解）从 KPI 中提取四个组件：水平、趋势、季节性、噪声，然后使用前三个组件的总和进行预测。 TSD 中值类似于 TSD，但它在计算这三个分量时使用中值而不是均值。小波分解（Wavelet decomposition）可以覆盖 KPI 的整个频域，我们将高频部分设置为预测。
大多数时间序列模型都有一个或多个参数，并且必须调整它们的参数以最适合 KPI。 但是，参数调整可能很耗时，并且通常需要领域知识。 在我们的研究中，我们的最终目标是确定波动相关性。 只要模型能够做出足够准确的预测，使得获得的波动特征能够捕捉到真实的波动模式，就没有必要争取最佳拟合参数。 因此，在 CoFlux 中，对于每个模型参数，我们根据经验枚举可能值的列表。 例如，Wavelet 的参数可以取几个可能的值。 对于每个参数配置（例如，win=1 天），Wavelet 模型可以生成一个预测 KPI，然后是一个波动特征。我们将具有特定参数配置的时间序列模型视为波动特征检测器。 总的来说，我们从表 1 所示的模型和参数配置中得到 86 个检测器。因此，对于每个 KPI，它们产生 86 个波动特征。
当然，如果需要，我们在 CoFlux 中的波动特征提取模块可以配置其他模型或参数值。 请注意，我们已经仔细评估了最广泛使用的时间序列模型。 通过我们的实验，我们发现其中一些，例如 MA（移动平均）、WMA（加权MA）和指数 WMA，在从我们的测试 KPI 中提取波动特征方面表现不佳，因为这些模型的预测主要是 依赖最近的数据，无法处理季节性 KPI。 图 4 显示了一个示例，MA 错误地将 KPI 主要模式中的季节性捕获为波动特征，从而导致误报。

特征放大

特征提取后，我们为每个 KPI 获得 86 个原始波动特征。 不同 KPI 的原始波动特征通常具有不同尺度和单位的值。 我们应用 z-score 对每个波动特征进行归一化。 归一化波动特征中的值越接近零，KPI 波动就越小。
通常，KPI 中的大多数值看起来都非常正常，并且主要由于噪声而与预测值略有不同。 为了减少噪音的影响，我们使用修正指数激活（方程 1）来加强大波动。 方程 1 放大显著偏离零的值，而对接近零的值几乎没有影响。 这种放大可以使波动特征更加可区分，并有助于波动相关性识别。 在CoFlux中，我们设置α=0.5（增长程度，值越大，增长越快）和β=10（如果|x|>β，f值不会增长）。 修正指数激活的有效性将通过实验进行评估，并在后面的章节中讨论。

相关性度量

互相关（Cross-correlation）是时间滞后时间序列的相似性度量，已广泛用于信号和图像处理。互相关可以很好地确定两个时间序列的形状相似度，同时考虑到它们在幅度和相位上的失真，适用于判断 CoFlux 中的三个问题。 因此，我们选择互相关来测量 CoFlux 中波动特征之间的相关性。 对于两个放大的波动特征$G=[g_1,g_2,\dots ,g_l]$和 $H=[h_1,h_2,\dots ,h_l]$，考虑到 G 和 H 沿时间轴的偏移，互相关始终保持一个向量（ 例如，H) 静态并使另一个（例如，G）滑过 H 以计算 G 的每个移位 s 的内积（其中
$s\in (-l,l)$,$l$是放大的波动特征的长度）。$G_s$是具有移位值$s$（尤其是$G_0=G$）的向量，可以表示为：

$G_s$和$H$的内积，以及它们的互相关值可以计算如下：
$R(G_S,H)={\sum }_{i=-l+1}^{l-1}{G}_S[i]\times H[i](3a)$
$CC(G_S,H)=\frac{R(G_S,H)}{\sqrt{R(G,G)\times R(H,H)}}(3b)$
枚举 s 的所有可能值，我们可以得到一个长度为$2l-1$的互相关值向量。设向量的最小值和最大值分别为$minCC$和$maxCC$ ，分别对应于移位值$s1$和$s2$。 那么 $G$和 $H$的最终互相关值可以表示为$FCC$：
$minCC=\underset{s}{\min }(CC(G_S,H)),s1=\underset{s}{argmin(CC(G_S,H))}(4a)$
$maxCC=\underset{s}{\max }(CC(G_S,H)),s2=\underset{s}{argmax(CC(G_S,H))}(4b)$

从方程3，我们知道$FCC\in [-1,1]$。 FCC 越接近 1 或 -1，G 和 H 之间的相关性越强。此外，正 FCC 表示它们沿同一方向移动，而负 FCC 表示一个波动特征增加而另一个减少，反之亦然。 互相关的有效性可以在后续实验中看到。

如算法 1 所示，通过放大波动特征，我们可以轻松分析两个 KPI 的波动相关性。 我们枚举所有放大的波动特征对来计算它们的互相关值。 在这些值中，选择绝对值最大的一个作为最终得分，并与阈值进行比较，以确定 KPI 之间是否存在波动相关性。 这个阈值可以由实际要求决定，或者由 precision-recall 曲线决定。 如果最终得分的绝对值低于阈值，则为$X\nsim Y$； 否则$X\sim Y$。 如果$X\sim Y$，我们继续找出时间顺序和方向。 时间顺序可以由 X 的移位值确定。如果它为零（即没有移位），则 X↔Y ； 如果为负（即 X 向左移动），则 X→Y ； 否则，Y→X。 这种波动相关性可以是正的也可以是负的，如最终得分所示。

模型验证

CoFlux 的数据集基本上是小于 60 条时间序列曲线。其中包括 CPU，错误率，错误数，内存使用率，成功率等不同的指标。


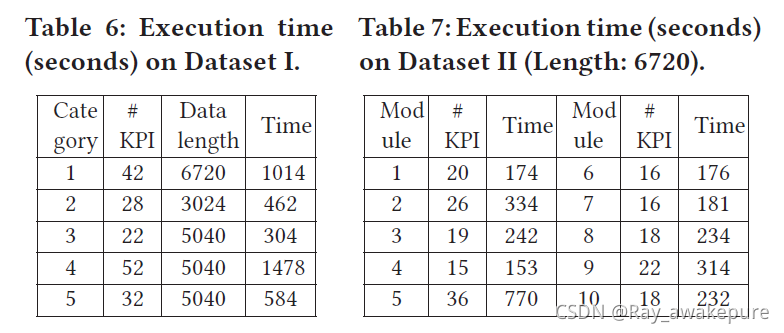
从运行时间上来看，对于一周的时间序列集合（< 60条）而言，CoFlux 基本上能够在 30 分钟内计算完毕，得到最终的运算结果。

其效果的评价指标是机器学习中的常见评价指标：准确率，召回率，F1_Score。

从 F1-Score 的评价指标来看，CoFlux 的效果优于其他算法。

相关引用文献

研究KPI之间的相关性的论文

标题：
Granger causality for time-series anomaly detection
摘要：
工业系统的最新发展为我们提供了来自传感器、日志、系统设置和物理测量等的大量时间序列数据。这些数据对于提供有关复杂系统的见解非常有价值，可用于早期检测异常.然而，这些时间序列数据的特殊性，如高维、变量间依赖复杂、数据量大等特点，对现有的异常检测算法提出了极大的挑战。在本文中，我们提出 Granger 图形模型作为一种有效且可扩展的异常检测方法，其结果可以很容易地解释。具体来说，格兰杰图形模型是一系列图形模型，它们通过将 L1 正则化学习应用于格兰杰因果关系来利用变量之间的时间依赖性。我们的目标是通过 Granger 图形模型有效地为每个变量计算一个强大的“相关异常”分数，该模型可以提供有关异常可能原因的见解。我们评估了我们提出的算法在合成和应用数据集上的有效性。结果表明，该算法的性能明显优于其他基线算法，并且对于大规模应用具有可扩展性

标题：Braid: Stream mining through group lag correlations
摘要：
目标是监控多个数字流，并确定哪些对与滞后相关，以及每个此类滞后的值。滞后相关（和反相关）很常见，而且在实践中非常有趣：例如，利率下降通常先于房屋销售增加几个月；若干年后，饮用水中含氟量越高，蛀牙就越少。其他设置包括网络分析、传感器监控、财务数据分析和移动对象跟踪。这样的数据流通常是相关的（或反相关的），但具有未知的滞后。我们提出了 BRAID，一种检测数据流之间滞后相关性的方法。 BRAID 可以处理半无限长的数据流，增量、快速、资源消耗小。我们还提供了一个理论分析，该分析基于 Nyquist 采样定理，表明 BRAID 可以几乎没有错误地估计滞后相关性，并且通常根本没有错误。我们对真实数据的实验表明，BRAID 在大多数情况下都能完美地检测到正确的滞后（最大相对误差约为 1%）；虽然它比简单的实现快 40,000 倍。

标题：Cyclostationarity: Half a century of research
摘要：
在本文中，简要介绍了关于循环平稳性的文献，并提供了广泛的参考书目。 包括已发表大量研究的所有语言的文献。 开创性的贡献是这样确定的。 引文分为 22 类，并按时间顺序列出。 处理信号分析的随机和非随机方法。 在经典的前者中，信号被建模为随机过程的实现。 在后者中，信号被建模为时间的单一函数，统计函数通过无限时间平均值而不是整体平均值来定义。 考虑了循环平稳性在通信、信号处理和许多其他研究领域的应用。

研究事件之间的相关性的论文

标题：Mining causality graph for automaticweb-based service diagnosis
摘要：
互联网公司提供高度可靠的基于网络的服务至关重要。基于 Web 的服务总是有许多组件运行在具有复杂交互的大规模基础设施中。作为高可靠性不可或缺的一部分，诊断仍然是一个棘手的问题。随着系统规模和复杂性的增长，它变得更加困难。在本文中，我们提出了一种基于因果关系图的自动诊断系统，以帮助系统操作员找到根本原因。因果关系图主要从监控系统的历史数据中提取，该方法包括四个步骤。 1）它利用数据挖掘方法提取初始因果关系图。 2) 一旦发生故障，它会根据因果关系图使用排名算法列出前 k 个嫌疑人。 3) 然后系统操作员检查嫌疑人并标记他们是对还是错。 4）监督学习算法将标签作为输入来调整因果关系图，以迭代地提高步骤2的诊断准确性。这种方法既不需要有关基于 Web 的服务的设计和实现细节的知识，也不需要检测服务的源代码。我们的受控实验表明，经过可数的学习迭代后，根本原因可以以 100% 的准确率排在前 3 名。

研究事件和KPI的相关性的论文

标题：Correlating events with time series for incident diagnosis
摘要：
随着在线服务越来越流行，事件诊断已成为最大限度减少服务停机时间和确保所提供服务质量的关键任务。对于大多数在线服务，事件诊断主要是通过分析运行时从服务中收集的大量遥测数据来进行的。时间序列数据和事件序列数据是遥测数据的两种主要类型。相关分析技术是工程师广泛用于数据驱动事件诊断的重要工具。尽管它们很重要，但以前很少有工作解决用于事件诊断的两类异构数据之间的相关性：连续时间序列数据和时间事件数据。在本文中，我们提出了一种评估时间序列数据和事件数据之间相关性的方法。我们的方法能够在事件诊断的背景下发现事件-时间序列相关性的三个重要方面：相关性的存在、时间顺序和单调效应。我们在模拟数据集和两个真实数据集上的实验结果证明了该算法的有效性。

VARMA模型

标题：Forecasting with varma models
摘要：
矢量自回归移动平均 (VARMA) 过程是用于生成时间序列变量集的线性预测的合适模型。 它们提供了线性数据生成过程的简约表示。 考虑在存在平稳变量和协整变量的情况下这些过程的设置。 此外，还提供了基于梯形形式的独特或识别的参数化。 讨论了模型规范、估计、模型检查和预测。 特别注意与同期和时间聚合的 VARMA 过程相关的预测问题。 比较基于聚合变量中的过去信息或分解信息的聚合变量的预测变量。

基础模型

CoFLUX的子模型

Diff

Holt-Winters

在做时序预测时，一个显然的思路是：认为离着预测点越近的点，作用越大。比如我这个月体重100斤，去年某个月120斤，显然对于预测下个月体重而言，这个月的数据影响力更大些。假设随着时间变化权重以指数方式下降——最近为0.8，然后0.82，0.83…，最终年代久远的数据权重将接近于0。将权重按照指数级进行衰减，这就是指数平滑法的基本思想。
指数平滑法有几种不同形式：一次指数平滑法针对没有趋势和季节性的序列，二次指数平滑法针对有趋势但没有季节性的序列，三次指数平滑法针对有趋势也有季节性的序列。“Holt-Winters”有时特指三次指数平滑法。

Historical average/median

TSD

Wavelet

用于对比的Baseline模型

J-measure

SIG

Pearson

Granger

Cross-correlation