【常用算法：进阶篇】15.O (1) 极速统计：揭秘整数末尾 0 的数量计算黑科技-CSDN博客

本文链接：https://blog.csdn.net/RickyIT/article/details/148067326

在这里插入图片描述

一、问题本质与应用场景

在计算机科学中，计算整数末尾0的数量是一个基础但高频的需求，广泛应用于：

数学计算：阶乘末尾0的数量、因式分解中10的因子统计；
位操作优化：二进制状态压缩、快速定位数据特征；
性能敏感场景：游戏引擎、大数据处理、密码学中的高频统计。

根据整数表示形式的不同，问题可分为两类：

十进制末尾0：由因子10（2×5）的个数决定，需统计因式分解中5的次数（因2的数量通常多于5）；
二进制末尾0：由最低位1的位置决定，需通过位运算直接定位。

二、十进制末尾0的统计：从O(k)到O(log n)的优化

1. 传统方法：循环取模的O(k)算法

核心思路：通过循环对整数取模10，统计末尾0的数量，直到余数不为0时终止。
代码实现（C++）：

int countTrailingZerosDecimalLoop(int num) {
    if (num == 0) return 1; // 特殊处理：部分场景定义0的末尾0数量为1
    int count = 0;
    while (num % 10 == 0 && num != 0) { // 排除num=0的死循环
        count++;
        num /= 10;
    }
    return count;
}

复杂度分析：

时间复杂度：O(k)，k为末尾0的数量（如10000需循环4次）；
空间复杂度：O(1)。

局限性：当k较大时（如num=10^20），需循环20次，无法满足高频调用的性能需求。

2. 数学优化：基于因子5的O(log n)算法

核心原理：十进制末尾0的数量等于整数因式分解中5的因子个数，公式为：
在这里插入图片描述

推导逻辑：

每5个数贡献1个5因子（如5,10,15,…）；
每25个数额外贡献1个5因子（如25=5×5），依此类推。

代码实现（C++）：

int countTrailingZerosDecimalMath(int n) {
    if (n == 0) return 1; // 特殊处理
    int count = 0;
    while (n >= 5) { // 当n<5时，后续项为0，无需计算
        n /= 5;
        count += n;
    }
    return count;
}

复杂度分析：

时间复杂度：O(log₅n)，循环次数为log₅n（如n=1e5时，循环次数为log₅1e5≈7）；
空间复杂度：O(1)。

关键对比：

维度	循环取模法	数学优化法
时间复杂度	O(k)	O(log n)
适用场景	小规模整数	大规模整数（如阶乘）
正确性	仅统计末尾0的个数	统计因子5的个数（适用于阶乘末尾0）

误区说明：

该方法并非严格O(1)，因循环次数随n增大而增加，但实际应用中常被称为“常数级优化”，因log₅n远小于k。

三、二进制末尾0的统计：从位运算到硬件级优化

1. 基础位运算：O(1)逻辑的初步实现

核心思路：

二进制末尾0的数量等于最低位1的位置（从0开始计数）；
通过n & -n提取最低位的1，利用补码特性实现。

补码原理：

负数在补码中表示为正数取反+1，因此n和-n的二进制仅在最低位1处相同，其余位互反；
例：n=104（0b1101000），-n补码为0b10011000，n & -n=0b0001000（即8）。

代码实现（Python）：

def countTrailingZerosBinaryBasic(n: int) -> int:
    if n == 0:
        return 0  # 0的二进制全为0，无有效末尾0（或根据需求返回32/64）
    least_one = n & -n  # 提取最低位的1
    return (least_one.bit_length() - 1)  # 计算位置

示例验证：

n=8（0b1000）：least_one=8，bit_length=4，返回3；
n=5（0b101）：least_one=1，bit_length=1，返回0。

2. 硬件级优化：De Bruijn序列实现真O(1)

核心思想：
利用De Bruijn序列的唯一性，将最低位1的位置映射到预定义的索引表，通过一次乘法和移位实现常数时间查询。

（1）De Bruijn序列基础

定义：长度为2^m的循环序列，包含所有m位二进制子序列各一次。例如，5位De Bruijn序列B(2,5)包含00000~11111的所有组合；
作用：将least_one的值（形如2^k）乘以De Bruijn常数后，高位m位唯一对应k值，可直接查表获取末尾0数量。

（2）代码实现（C语言，32位整数）

unsigned int countTrailingZerosBinaryDeBruijn(unsigned int v) {
    if (v == 0) return 32; // 特殊处理：0的二进制有32个0（依平台而定）
    // De Bruijn序列对应的查表法（适用于32位无符号整数）
    static const int DeBruijnTable[32] = {
        0, 1, 28, 2, 29, 14, 24, 3, 30, 22, 20, 15, 25, 17, 4, 8,
        31, 27, 13, 23, 21, 19, 16, 7, 26, 12, 18, 6, 11, 5, 10, 9
    };
    unsigned int least_one = v & -v; // 提取最低位的1
    // 乘以De Bruijn常数，右移27位获取高5位索引
    unsigned int index = ((unsigned int)((least_one * 0x077CB531U) >> 27));
    return DeBruijnTable[index];
}

（3）关键步骤解析

乘法运算：least_one * 0x077CB531U
- 0x077CB531的二进制是De Bruijn序列B(2,5)的压缩表示，确保乘积的高5位唯一对应k值；
移位与索引：>>27截取高5位（32位整数中，2^30是最大的2的幂，5位足够表示0-31）；
查表映射：通过预定义的DeBruijnTable将索引转换为末尾0数量。

（4）性能优势

真O(1)时间：仅需一次乘法、移位和查表，耗时为硬件指令周期（纳秒级）；
扩展性：64位场景可通过更大的De Bruijn常数（如0x03f79d71b4cb0a89U）和64项查表扩展。

四、核心方法对比与选型指南

1. 十进制vs二进制：需求决定解法

场景	核心需求	推荐方法	时间复杂度	关键代码片段
阶乘末尾0的数量	统计因子5的个数	数学优化法（O(log n)）	O(log₅n)	`while (n >= 5) { n/=5; count+=n; }`
二进制状态末尾0统计	快速定位最低位1的位置	位运算基础法（O(1)）	O(1)	`least_one = n & -n; return bit_length()-1;`
高频二进制统计（如GPU）	硬件级原子操作	De Bruijn查表法（真O(1)）	O(1)	`index = (least_one * 0x077CB531U) >> 27;`

2. 特殊情况处理策略

输入为0：
- 十进制：通常视为特殊值，返回1或0（需根据业务定义）；
- 二进制：32位系统返回32，64位系统返回64，或抛出异常。
负数输入：
- 十进制：直接取绝对值处理；
- 二进制：先转为无符号数（如C语言中unsigned int v = (unsigned int)n;），避免符号位干扰。

五、工程实践：从代码到硬件的优化路径

1. 十进制优化：预计算提升效率

场景：当需要多次计算不同整数的末尾0数量时，可预计算5的幂次（如5,25,125,…），避免重复除法。
代码优化（Python）：

# 预计算5的幂次列表（最大支持n=1e18）
POW5 = [5**i for i in range(1, 32) if 5**i <= 1e18]

def countTrailingZerosDecimalPrecompute(n: int) -> int:
    if n == 0:
        return 1
    count = 0
    for pow5 in POW5:
        if pow5 > n:
            break
        count += n // pow5
    return count

2. 二进制极致优化：SIMD并行处理

思路：利用CPU的SIMD指令（如SSE/AVX）同时处理多个整数的末尾0统计，例如：

用SSE指令一次处理4个32位整数，通过掩码和批量查表实现并行计算。
伪代码示例：

// 假设__m128i是SSE的128位向量类型
__m128i count_trailing_zeros_simd(__m128i v) {
    __m128i least_one = _mm_and_si128(v, _mm_set1_epi32(-1)); // 提取每个整数的最低位1
    // 此处需结合De Bruijn查表的向量化版本（实际实现复杂，需汇编或intrinsics）
    return _mm_shuffle_epi32(least_one, 0); // 示例：返回各整数的末尾0数量
}

3. 跨语言实现：Python的位运算优化

挑战：Python的整数无固定位数，需处理大整数的末尾0统计。
解决方案：

def countTrailingZerosBinaryPython(n: int) -> int:
    if n == 0:
        return 0
    # 转换为二进制字符串，去除前缀'0b'后从末尾统计0
    binary_str = bin(n)[2:]
    return len(binary_str) - len(binary_str.rstrip('0'))

局限性：时间复杂度为O(log n)，适用于非性能敏感场景。

六、扩展应用与前沿技术

1. 组合数学：阶乘末尾0的批量计算

问题：计算n!末尾0的数量，等价于统计1~n中5的因子个数。
优化公式：
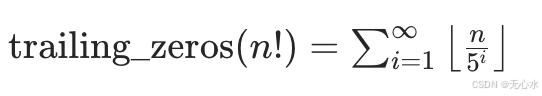
在这里插入图片描述

代码实现（Python）：

def factorialTrailingZeros(n: int) -> int:
    count = 0
    while n > 0:
        n //= 5
        count += n
    return count

2. 密码学：RSA密钥生成中的因子统计

在RSA算法中，需统计大整数因式分解中2和5的次数，以判断密钥的合法性。此时可结合：

十进制方法统计5的次数；
二进制方法统计2的次数（等价于二进制末尾0的数量）。

3. 前沿方向：量子计算中的位模式匹配

量子位（Qubit）的状态统计可借鉴De Bruijn序列的思想，通过量子并行性实现O(1)时间的末尾0统计，但目前仍处于理论研究阶段。

七、关键知识点总结

技术点	十进制场景	二进制场景	核心代码特征
基础算法	循环取模（O(k)）	循环右移（O(log n)）	简单直观，适用于教学和小规模数据
数学优化	因子5统计（O(log n)）	补码提取最低位1（O(1)）	利用数学规律减少循环次数
硬件级优化	无（依赖数学特性）	De Bruijn查表法（真O(1)）	结合硬件特性实现原子操作
特殊处理	0视为1个0，负数取绝对值	0返回32/64，负数转无符号数	边界条件决定算法鲁棒性

八、课后练习与思维拓展

1. 实战题目

题目1：计算1000!的末尾0数量（需处理大数，Python实现）。
题目2：用De Bruijn序列法实现64位整数的二进制末尾0统计（提示：查找64位De Bruijn常数）。
题目3：优化十进制算法，使其能处理n=0的特殊情况（返回0或1需明确业务定义）。

2. 深度思考

为什么二进制方法无法直接用于十进制末尾0统计？
答：十进制末尾0由因子10决定，需同时考虑2和5的因子，而二进制方法仅反映2的因子次数（末尾0的数量等于二进制中2的因子次数）。
如何证明De Bruijn序列法的正确性？
答：通过数学归纳法证明每个2^k对应的乘积高位唯一映射到k值，结合De Bruijn序列的定义确保无冲突。