2016.8.7+8.8+8.9+8.10+8.12 炒鸡无敌程序大集合

总结一下，这几天的学习情况大概是这样的。
8.7：后缀数组
8.8：字典树
8.9：最大流
8.10：考试（无内容）
8.12：组合数学+拓扑图+强连通分量

后缀数组

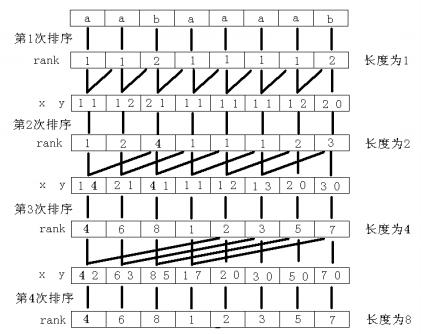
　　后缀数组的主要内容就是两个算法：倍增算法以及基数排序。这是两个很马叉虫的算法。
　　先阐述一下倍增算法。这是一个对字符串以及其后缀排序大小的排序，速度灰常快，只需要执行$logN$次。这是一个怎么样的排序呢？
　　是这样的，首先我们根据字符串S的每一个字符串长度为1的字符串进行比较，不用多说，这是线性时间就可以得出的结果。然后，我们可以发现，只根据第一个字母排序是不能得出每一个字符串的唯一大小的。所以我们要进行其他的高级运算。
　　在得出字符串长度为1时的大小之后，我们就可以通过获取第2位，或者说得到总长度为2（其实应该叫做$2^1$）的字符串。由于我们之前已经得到了每一个长度为1字符串的大小，我们就能通过双关键字排序，其实也不完全是，就是根据已经存在的长度为1的字符串大小得出长度为2的字符串的大小，这依旧是线性时间就能得出的。
　　然后就很好理解了，既然$2^1$这个东西存在，那么它就有它存在的意义。为什么这样称呼2呢？这还不简单吗？看名字就知道了啊！既然是倍增算法，那么肯定是倍增的啊！为什么是倍增呢？因为当我们处理完长度为2的字符串的大小关系（这里还不用管字符串的大小是否唯一），我们就可以直接得出每一个长度为2的字符串的大小，那么问题来了。2+2=？不就是4 lor~然后，如此类推，当我们得到长度为4的字符串大小关系的答案时，我们就可以得出4+4=8长度的字符串的大小。所以这个算法只需要$NlogN$的时间就可以解决这个问题。
　　如果还不懂，那就来看我这张从度娘那盗来的图吧~
　　
　　
　　解决了倍增算法，我们就来了解一下什么是基数排序吧。这也是个很有趣的东西。
　　何谓基数排序，那就是一个根据基（础）数（据）加上后来的辅助数据来解决一些多关键字排序的问题。其实叫做基数排序，我感觉就是桶排序的加强版。因为桶排序是储存一个关键字，其实也就是直接得出答案。而基数排序就要记录多个关键字，然后将它们合并。因为这些数据是不变的，是固定的，而且基数排序只是自身的后缀进行处理，也就是倍增算法的具体操作罢了。所以，我们就开始解决这个简单且simple的问题吧。
　　首先，基数排序也是需要用第一次的数据做基础的，从倍增算法中我们可以得知，这很简明易懂。

Next Day

=================请叫我分割线=================

字典树

　　字典树，字典树，顾名思意，就是一棵像字典一样的树。而每一条边记录的都是各种的字符。总而言之就是一种对不同字符的处理和解决。反正就是一种很朴素的方法，存放的时间为字符串总长度，储存空间一般是存储 总长度*字符数（26之类的）。
　　好吧好吧。我承认我不太会讲这个辣么简单的东西。所以我只好来讲讲关于字典树的构造方法吧。
　　字典树的构造方法有两种。
　　第一种是用邻接矩阵的方法，直接开 长度*字符状态 的空间大小，第一维用来做数组模拟链表的下标，然后第二维用来做字符状态的转移和限制，这个二维数组里面有一个一定要记的值，就是指向下一层的下标，因为只有记录这个才能把这个数组模拟成链表，不然直接用下标来做字典树的话就不叫链表了。虽然这种方法很简单也很常见，但是有某些阴险狡诈，卑鄙无耻的出题人总爱用这种硬性的空间卡你的数据范围，按理来说只开 长度 个空间其实就可以存储所有的内容了，但是为了记录状态我们又不得不开多一维。那么问题来了，这道题既然放在这，那就一定又解决的办法，是什么呢？就是我们神奇的指针大法！
　　第二种，没错就是指针。指针是个好东西啊！因为指针不需要事先开好数组，只需要每一次访问到一个新的节点就从空间里申请一个节点，把指针指向新节点的地址，然后这个新的节点就可以拿来用了。所以指针基本上就只需要用 长度 个空间就可以解决这个问题。具体怎么实现呢？其实跟第一种方法是一样的，也是用链表的方法，记录他的下一个，然后把他们链接起来就形成一个跟第一种方法一样的链表了，唯一不同的是，第一种是事先开好空间大小，而第二种则是每次访问到需要一个新的节点的时候，就申请一个新的节点。
　　差不多就是这样了，我觉得还是举个例子加强一下印象吧。
　　例如说，求‘aab’‘aabaa’‘aca’这三个字符串的最长公共前缀，怎么办呢？
　　看下图。
　　
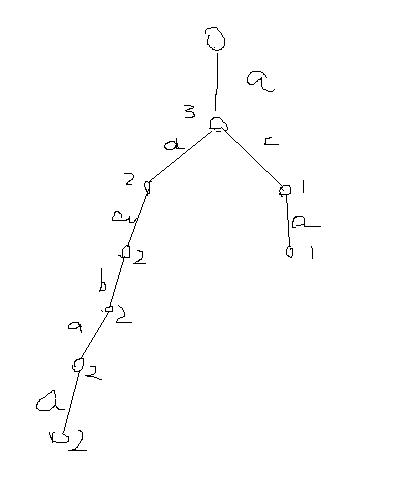
　　讲述的是一段凄婉的爱情故事，啊呸，什么东西卡在我喉咙里。讲述的是把这几个字符串放进字典树后的样子，而每一个节点上都记录一个数值，那就是被经过的次数，我们可以看到，根结点下面那个点被经过了三次，就说明他是所有字符串的公共前缀，然后在看到下面一层，发现左边是被经过了两次，另一边是被经过了一次，所以就不是公共前缀了啊！所以我们只需要从根节点往下数，数到一个被访问次数小于前面的节点，那么从他的上一层到根结点都是这些字符串的最长公共前缀。
　　贴段程序压压惊~
　

题目意思很清楚：就是判断输入的电话号码中是否有号码是其他号码的前缀，很显然要用到字典树。根据分析可知:
如果字符串Xn=X1X2….Xn是字符串Ym=Y1Y2….Ym的前缀，有在插入的时候有两种情况:Xn在Yn之前插入，Xn在Yn之后插入。
1)如果Xn在Yn之前插入，那么在插入Yn的时候必然经过Xn的路径，此时可以根据判断在这条路径上是否已经有结点被标记已经构成完成的字符串序列来判断是否存在Yn的前缀；
2)如果Xn在Yn之后插入，那么插入完成之后当前指针指向的结点的数组中的元素必定不全为0。
这是一道模板题，不需要多说什么废话。

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std ;
int point=0;
int val[10001*10][15];
int tree[10001*10][15];
char chr[10005][15];
bool check(char *a)
{
    int len=strlen(a);
    int p=0,state;
    for (int i=0;i<len;i++)
    {
        int now=a[i]-'0';
        if (i==len-1) state=-1;
            else state=1;
        if (val[p][now]==-1)
            return 0;
        if (val[p][now]==1&&state==-1)
            return 0; 
        if (tree[p][now]==0)
        {
            tree[p][now]=++point;
            val[p][now]=state;
        }
        p=tree[p][now];
    }
    return 1;
}
int main()
{
    int t;
    scanf("%d",&t);
    while (t--)
    {
        point=0;
        memset(tree,0,sizeof tree);
        memset(val,0,sizeof val);
        int n;
        scanf("%d",&n);
        for (int i=0;i<n;i++)
            scanf("%s",chr[i]);
        bool flag=1;
        for (int i=0;i<n;i++)
        {
            flag=check(chr[i]);
            if (!flag)
            {
                printf("NO\n");
                break;
            }
        }
        if (flag)
        {
            printf("YES\n");
        }
    }
    return 0;
} 

就是这样。
下一题走你！
【下一题是一道用第一种方法会被卡空间范围的题目，所以我用指针来做，让你们在座的各位辣鸡见识一下】

题意是给定如干个字符串，将其两两组合，有n × n种组合方式，求有多少个回文组合。
You can assume that the total length of all strings will not exceed 2,000,000. Two strings in different line may be the same.
需要注意的就是那一串数字，你没有看错，长度就是这么长，足足又两百万！！额，好吧，是一共两百万个字符~
然后，就没有然后了，这个数据范围还是比较大的。
所以指针走你。

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std ;
const int N=2000002;
struct Trie
{
    int val,num;
    Trie *nxt[27];
};
Trie node[N];
Trie *root;
int begin[N],end[N],d[N*2+10];
char S[N],T[N],now[N*2+10];
bool flag[2][N],tmp[N*2+10];
long long ans=0;
int pos=0;
void manachar(char *a,bool *ok)
{
    int len=strlen(a);
    now[0]='!';
    now[1]='z'+1;
    for (int i=0,j=1;i<len;i++)
        now[++j]=a[i],now[++j]=now[1];
    len=strlen(now);
    int r=0,mid=0;
    for (int i=1;i<len;i++)
    {
        if (r>i)
            if (d[2*mid-i]<r-i)
                d[i]=d[2*mid-i];
            else d[i]=r-i;
        else d[i]=1;
        while(now[i-d[i]]==now[i+d[i]])
            d[i]++;
        if (i+d[i]>r)
            r=i+d[i],mid=i;
    }
    int j=0;
    for (int i=0;i<len;i++)
        if (i+d[i]==len&&i!=len-1)
            tmp[i-d[i]]=1;
    for (int i=0;i<len;i++)
        if (now[i]>='a'&&now[i]<='z'||now[i]=='!')
            ok[j++]=tmp[i];
    ok[j-1]=0;
    for (int i=0;i<len;i++) 
        d[i]=0,now[i]=0,tmp[i]=0;
}
void add(char S[],int l,int r)
{
    Trie *temp=root;
    for (int i=l;i<=r;i++)
    {
        int ch=S[i]-'a';
        temp->val+=flag[0][i];
        if (temp->nxt[ch]==NULL)
            temp->nxt[ch]=&node[pos++];
        temp=temp->nxt[ch];
    }
    ++temp->num;
}
void query(char S[],int l,int r)
{
    Trie *temp=root;
    for (int i=l;i<=r;i++)
    {
        int ch=S[i]-'a';
        temp=temp->nxt[ch];
        if (temp==NULL) break;
        if ((i<r&&flag[1][i+1])||i==r)
            ans+=temp->num;
    }
    if (temp) ans+=temp->val;
}
int main()
{
    int n,l,L=0;
    scanf("%d",&n);
    root=&node[pos++];
    for (int i=0;i<n;i++)
    {
        scanf("%d",&l);
        scanf("%s",S+L);
        for (int j=0;j<l;j++)
            T[L+j]=S[L+(l-1-j)];
        begin[i]=L;
        end[i]=L+l-1;
        manachar(S+begin[i],flag[0]+begin[i]);
        manachar(T+begin[i],flag[1]+begin[i]);
        add(S,begin[i],end[i]);
        L+=l;
    }
    for (int i=0;i<n;i++)
        query(T,begin[i],end[i]);
    printf("%lld\n",ans);
    return 0;
}

大力戳我！没错要题目就是要戳这里！
【妈卵，懒得翻译了，直接给链接自己看题目sa~

　　还有一道很有意思的题目，是一道存储二进制状态的题。这道题是一道在树上做的题【咳咳，别想太多，在树上你怎么做题？】这道题要求在一棵树上任意两个点的路径异或和最大！！！
　　这道题是字典树？字典树？字典树？没错，还真是。首先我们要解决的是，将这个问题转化一下，变成另一个样子。我们知道，X^X=0【不懂的小伙伴让老司机度娘带你去科普】所以当两个节点同时连接根结点的时候，这两条路的异或和正好等于它们到根结点这两条路的异或和。是不是很神奇，其实就相当于把他们最近公共祖先到根结点的路径异或和去掉了，所以不会有什么影响。啊呸，谁说没有影响的，这就可以把问题转化成求这棵树上每一个点到公共祖先的路径异或和了！然后我们就可以把这些异或和放进字典树中。有人肯定要问，不都是一个数字吗？怎么放啊？切，那你就把它变成N个数字lor。因为异或这种运算是相同为“1”，不相同为“0”的。所以我们就可以把它们的二进制放进去，然后就很简单了。我们把所有路径异或和放进字典树后，我们就可以根据枚举所有到根节点的路径异或和然后找字典树里面尽量跟这个数相反，也就是异或为“1”的数。但是还有一个小细节需要注意，那就是最大数据也只有30位，因为<2^31所以只有30位，所以我们就需要把这30位都记录下来，因为高位的大小比后面的更能影响整个数的大小。
　　例如说：
　　10000
　　01111
　　即使后面的全都满足又怎么样？老子，啊呸，劳资第一位就比你大，你能咋地？嗯？不服？嗯，没错，就是这种情况。
　　
程序走你！【注：因为没有卡空间大小，所以我就懒得用指针了。

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std ;
int edge[4*100001],edgew[4*100001],Next[4*100001];
int head[2*100001],sum[2*100001],tree[35*100001][3];
bool go[2*100005];
int e=0,point=0;
void addedge(int u,int v,int w)
{   
    edge[e]=v; Next[e]=head[u]; edgew[e]=w; head[u]=e++;
    edge[e]=u; Next[e]=head[v]; edgew[e]=w; head[v]=e++;
}
void dfs(int k,int val)
{
    sum[k]=val;
    go[k]=1;
    for (int i=head[k];i!=-1;i=Next[i])
    {
        if (!go[edge[i]])
            dfs(edge[i],edgew[i]^val);
    }
}
void add(int val)
{
    int p=0; 
    for(int i=30;i>=0;i--)
    {
        int state=0;
        if (val&(1<<i))
            state=1;
        if (!tree[p][state])
            tree[p][state]=++point;
        p=tree[p][state];
    } 
}
int query(int val)
{
    int p=0;
    int num=0;
    for (int i=30;i>=0;i--)
    {
        int state=0;
        if (val&(1<<i)) 
            state=1;
        if (tree[p][1-state])
        {
            num|=1<<i;
            p=tree[p][1-state];
        }
        else p=tree[p][state];
    }
    return num;
}
void clean()
{
    memset(edge,0,sizeof edge);
    memset(edgew,0,sizeof edgew);
    memset(Next,0,sizeof Next);
    memset(head,-1,sizeof head);
    memset(tree,0,sizeof tree);
    memset(go,0,sizeof go);
    memset(sum,0,sizeof sum);
}
int main()
{
    int n; 
    while (~scanf("%d",&n))
    {
        point=0;
        clean();
        for (int i=0;i<n-1;i++)
        {
            int u,v,w;
            scanf("%d%d%d",&u,&v,&w);
            addedge(u,v,w);
        }
        dfs(1,0);
        for (int i=0;i<n;i++)
            add(sum[i]);
        int ans=0;
        for (int i=0;i<n;i++)
            ans=max(ans,query(sum[i]));
        printf("%d\n",ans);
    }
    return 0;
}

Next Day

=================请叫我分割线=================

最大流

最大流的概念：这个东西主要是拿来处理一个有源点和汇点的一个有u个点，v条边的有向图G(u,v)。每条边上面都有一个权值，当这条边流过了一定的东西之后，是不能再通过这条边流其他东西了，而这个决定能不能流【咳咳，don’t think too more】就在于它的流量是多少。所以怎样使流到汇点的值最大就是这个算法的存在意义。

最大流的一些小技巧：因为这不是什么神奇的算法，也不是那种一股脑可以完成的东西，所以我们就需要一个【悔棋】按钮。啊呸，说马叉虫话。总之就是这个意思，我们需要将一些流量等价的从另外一个方向流出去，这是可行的！至于怎么完成，可以透露的是，这叫做反向边，正向边的残量减少时，反向边的残量就增加。这是相对应的。然后就是因为这个东西，我们就会使用大量的时间去反复更新。

【注：还有一些需要注意，这是我第一次做的时候错误的地方，挺值得分享的。
那就是，流量是相对于边来说的，而不是一个点，一个点是不叫做流量的。
还有我们只需要记录一个残量就足够了，因为残量=总量-已用流量。记录一个值明显比两个好多了。
还有还有，要记录每一条边上的最小瓶颈，因为根据木桶原理，流量的多少不是根据最长的那条边，而是最短的那条边决定的。
最后，要记得将数组清空。

啊！终于熬到贴程序的地方了！
依旧是放题目链接：
没错，要题目就猛戳这里！！！

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std ;
int n,m;
int re[205],from[205],a[205][205],que[2000000];
bool go[205];
int maxstream(int s,int t)
{
    memset(que,0,sizeof que);
    int sum=0;
    while (true)
    {
        memset(go,0,sizeof go);
        memset(re,0,sizeof re);
        go[s]=1;
        re[s]=100000000;
        int head=0,tail=0;
        que[0]=s;
        while (head<=tail)
        {
            int u=que[head];
            head++;
            for (int i=1;i<=t;i++)
            {
                if (!go[i]&&a[u][i]>0)
                {
                    go[i]=1;
                    que[++tail]=i;
                    from[i]=u;
                    re[i]=min(re[u],a[u][i]);
                }
            }
        }
        if (re[t]==0) break;
        for (int i=t;i!=s;i=from[i])
        {
            a[i][from[i]]+=re[t];
            a[from[i]][i]-=re[t];
        }
        sum+=re[t];
    }
    return sum;
}
int main()
{
    while (~scanf("%d%d",&n,&m))
    {
        memset(a,0,sizeof a);
        for (int i=1;i<=n;i++)
        {
            int u,v,w;
            scanf("%d%d%d",&u,&v,&w);
            a[u][v]+=w;
        }
        printf("%d\n",maxstream(1,m));
    }
    return 0;
}

差不多就这样了。
嗯。

Next Day

=================请叫我分割线=================

考试总结

　　蛤蛤蛤蛤蛤！
　　好吧，155分没什么好笑的。做了三题，第一题本该满分的。没错说得的就是你，出题人，看什么看？要不是你的mod没有写上去，我会只有这么一丢丢分？然后，第二题，理所当然的满分了。第三题就有点坑爹了。我的flag立错位置了，所以大部分数据都没过，而且我的这个算法是有那么一丢丢的问题，很容易超市，需要在处理一个反向next【这道题是KMP】才能达到O(N)级别的算法。不然的话就要用扩展KMP来做。坑爹的题目说了巴拉巴拉一大堆，然后又说KMP，KMP，KMP，别™KMP了伤身又伤肾【咳咳，没什么，就当没看见】。于是我就天真的用KMP来做了。前面的做法与标程一致，只不过少处理了一个数组，时间复杂度升了一维，其实好运的话可以卡过比较多的数据的。至于第四题，还有五分钟，看看题目消遣消遣就好。【消音】【消音】【消音】的，要不是为了看懂第一题浪费了我这么多时间，我会介么惨？？？好吧，最后一题其实也就是搜索加最大流，因为最大流只能处理二分图，所以我们要把三分图【乱入的名字】合并成二分图。由于木桶原理，最后的答案是由最短的那个决定的【第一次看见短小有人权啊！没什么，当我没说】于是我们在把三分图读入进二分图的时候，我们需要在两个节点之间去min值。然后最大流！最大流！最大流！嗯。就是这样。
　　先看题【为什么没有链接！！为什么！！为什么！！】

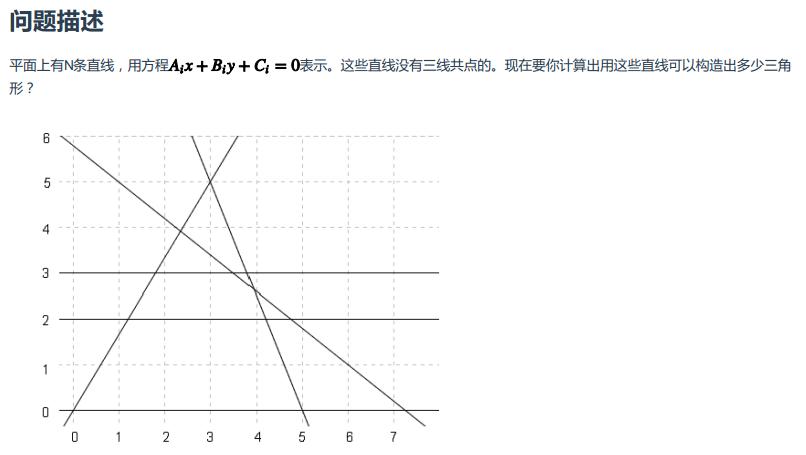
　　大小不一，别怪我，要怪就怪画图软件，怪windows系统，不关我事，尽情甩锅。

好了，又是贴程序的欢乐时光。

#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std ;
struct Tline
{
    double xl,yloc;
}line[300005];
long long val[300005];
bool cmp(Tline a,Tline b)
{
    return a.xl<b.xl;
}
int main()
{
    freopen("trokuti.in","r",stdin);
    freopen("trokuti.out","w",stdout);
    int n;
    cin>>n;
    for (int i=0;i<n;i++)
    {
        double a,b,c;
        cin>>a>>b>>c;
        line[i].xl=-a/b;
        line[i].yloc=-c/b;
    }
    sort(line,line+n,cmp);
    int flag=1;
    val[flag]=1;
    for (int i=1;i<n;i++)
    {
        if (line[i].xl==line[i-1].xl)
        {
            if (line[i].yloc!=line[i-1].yloc)
                val[flag]++;
        }
        else val[++flag]++;
    }
    long long tmp=(flag-1)*(flag-2)/2;//=(flag)*(flag-1)*(flag-2)/6*3/flag
    long long ans=(flag)*(flag-1)*(flag-2)/6;
    for (int i=1;i<=flag;i++)
            ans+=(val[i]-1)*tmp;
    cout<<ans<<endl;
    return 0;
}

　　至于哪里需要mod，什么时候要重测，嗯根本就没有说过嘛，懂你的。

程序猿走你！

#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std ;
const int INF=2000000000;
struct Tbe
{
    int a,b,c=0;
}be[100005];
struct Tstack
{
    int want,costl,costr,num;
}stack[100005*10];
int cost[10005],begin[10005],end[10005];
bool cmp(Tbe a,Tbe b)
{
    return a.c<b.c;
}
int main()
{
    freopen("dwarf.in","r",stdin);
    freopen("dwarf.out","w",stdout);
    int n,m;
    cin>>n>>m;
    for (int i=1;i<=n;i++)
        cin>>cost[i];
    for (int i=1;i<=m;i++)
        cin>>be[i].c>>be[i].a>>be[i].b;
    sort(be+1,be+m+1,cmp);
    be[0].c=be[1].c-1;
    be[m+1].c=be[m].c+1;
    for (int i=1;i<=m+1;i++)
        if (be[i].c!=be[i-1].c)
        {
            begin[be[i].c]=i;
            end[be[i-1].c]=i-1;
        }
    int top=1;
    int flag=1;
    stack[1].want=0;
    stack[1].costl=cost[1];
    stack[1].num=1;
    stack[1].costr=0;
    while(flag<=top)
    {
        int now=stack[flag].num;
        for (int i=begin[now];i!=0&&i<=end[now];i++)
        {
            top++;
            stack[top].want=flag;
            stack[top].num=be[i].a;
            stack[top].costl=cost[be[i].a];
            stack[top].costr=INF;
            top++;
            stack[top].want=flag;
            stack[top].num=be[i].b;
            stack[top].costl=cost[be[i].b];
            stack[top].costr=INF;
            stack[flag].costr=0;
        }
        flag++;
    }
    while(top)
    {
        int now=stack[top].num;
        int nxt=stack[top].want;
        for (int i=begin[now];i<=end[now];i++)
            stack[top].costl=min(stack[top].costl,stack[top].costr);
        stack[nxt].costr+=stack[top].costl;
        top--;
    }
    cout<<stack[top+1].costl<<endl;
    return 0;
}

AC不解释，就是这么强！

让你们感受下被炒鸡长的题目支配的恐惧吧！

又是一段不AC的代码。。。
不过我知道怎么做也懒得改了。。。
就是这么懒，就是这么任性。

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std ;
const int mod=1000000007;
char chr[1000005];
int Next[1000005],num[1000005];
int main()
{
    freopen("zoo.in","r",stdin);
    freopen("zoo.out","w",stdout);
    int t;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%s",chr);
        int len=strlen(chr);
        Next[0]=Next[1]=0;
        int k=0;
        for (int i=1;i<len;i++)
        {
            while (k>0&&chr[i]!=chr[k])
                k=Next[k];
            if (chr[i]==chr[k]) k++;
            Next[i+1]=k;
        }
        num[0]=0;
        int flag=0;
        for (int i=1;i<len;i++)
        {
            num[i]=num[Next[i]];
            if ((Next[i]==0&&chr[i]==chr[0])||Next[i]!=0)
            {
                int tmp=i;
                while (!(Next[tmp]<=flag))
                    tmp=Next[tmp];
                if ((i+1)/2>Next[tmp]) 
                {
                    num[i]++;
                    flag=Next[tmp]+1;
                }
            }
        }
        long long ans=1;
        for (int i=0;i<len;i++)
            ans=(ans*(num[i]+1))%mod;
        printf("%lld\n",ans);
    }
    return 0;
}

最后一题求大神check一下，感觉是没错的。但是不是超时就是错…

蛤蛤蛤蛤蛤，换文本了，是不是很气啊~
咳咳，题目太长了，你叫我怎么截图？？
太小你们又看不见。

样例输入
15 15 15
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 1 1 1 1 1 1 1 1 1 0 1 1 1 1
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 1 1 1 1 1 1 1 1 1 0 1 1 1 1
1 1 1 1 1 1 1 1 1 1 0 1 1 1 1
1 1 1 1 1 1 1 1 1 1 0 1 1 1 1
1 1 1 1 1 1 1 1 1 1 0 1 1 1 1
1 1 1 1 1 1 1 1 1 1 0 1 1 1 1
1 1 1 1 1 1 1 1 1 1 0 1 1 1 1
1 1 1 1 1 1 1 1 1 1 0 1 1 1 1
1 1 1 1 1 1 1 1 1 1 0 1 1 1 1
1 1 1 1 1 1 1 1 1 1 0 1 1 1 1
1 1 1 1 1 1 1 1 1 1 0 1 1 1 1
1 1 1 1 1 1 1 1 1 1 0 1 1 1 1
1 1 1 1 1 1 1 1 1 1 0 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
样例输入
13

错误代码还有三十秒到达战场，碾碎它们。
全军出击~

#include<queue>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int INF=2100000000;
int G,B,P;
int level[100];  
bool bg[100][100],bp[100][100],pg[100][100];
struct Tdinic
{
    int c,f;
}edge[100][100];
bool dinic_bfs()
{
    queue<int>Q;
    memset(level,0,sizeof level);
    Q.push(0);
    level[0];
    int u,v;
    while (!Q.empty())
    {
        u=Q.front();
        Q.pop();
        for (v=1;v<=G;v++)
        {
            if (!level[v]&&edge[u][v].c>edge[u][v].f)
            {
                level[v]=level[u]+1;
                Q.push(v);
            }
        }
    }
    return level[G];
}
int dinic_dfs(int u,int cp)
{
    int tmp=cp;
    int v,t;
    if (u==G)
        return cp;
    for (v=B;v<=G&&tmp;v++)
    {
        if (level[u]+1==level[v])
        {
            if (edge[u][v].c>edge[u][v].f)
            {
                t=dinic_dfs(v,min(tmp,edge[u][v].c-edge[u][v].f));
                edge[u][v].f+=t;
                edge[v][u].f-=t;
                tmp-=t;
            }
        }
    }
    return cp-tmp;
}
int dinic()
{  
    int sum,tf;
    sum=tf=0;
    while(dinic_bfs())
    {
        while(tf=dinic_dfs(1,INF))
            sum+=tf;
    }
    return sum;
} 
int main()
{
    freopen("freeopen.in","r",stdin);
    freopen("freeopen.out","w",stdout);
    memset(edge,-1,sizeof edge);
    scanf("%d%d%d",&G,&B,&P);
    for(int i=1;i<=G;i++)
        for(int j=1;j<=B;j++)
            scanf("%d",&bg[j][i]);
    for (int i=1;i<=G;i++)
        for(int j=1;j<=P;j++)
            scanf("%d",&pg[j][i]);
    for (int i=1;i<=B;i++)
        for(int j=1;j<=P;j++)
            scanf("%d",&bp[i][j]);
    for (int i=1;i<=B;i++)
        for (int j=1;j<=P;j++)
            if (bp[i][j])
                for (int k=1;k<=G;k++)
                    if (bg[i][k]&&pg[j][k])
                        edge[i][B+k].c=1;
    G=G+B+1;
    for (int i=1;i<=B;i++)
        edge[0][i].c=0;
    for (int i=B+1;i<G;i++)
        edge[i][G].c=0;
    printf("%d\n",dinic());
    return 0;
}

啊啊啊啊啊！

Next Day

=================请叫我分割线=================

组合数学

　　其实都没什么东西学，早都学过了，但还是总结一下吧。
　　总结个屁。
　　哼唧，就是这么膨胀，地心引力根本抓不住我。
　　我就是要上天，和太阳肩并肩。
　　详情请见：戳我你就上天了

下一个！

拓扑图+强连通分量

　　
　　这个就很高级了。其实还不是那【消音】样。所谓拓扑图，就是一些点，分别指向另一个点，然后每个点有入度和出度。但是还有可能形成环。所谓强连通分量，其实不要被这个名字吓到，他只是虚有其表罢了。很简单很simple的。其实就是指一个图是完全连通的，算了，先说连通分量吧。连通分量就是拓扑图中，为什么叫拓扑图，就是因为他是可以拓扑排序的，然后把入度为0的点全部删掉，最后会剩下一个环或者多个环，然后，这些环就叫做连通分量，而所有的环可以互相连接时，这些东西就叫做强连通分量。
　　好了，让我来告诉你，强连通分量有什么用吧。
　　例如说：有N个人，每个人都有他自己心目中的老大。假如A认为B是老大，B认为C是老大，那么C就是A的老大。依此类推。但是，如果A认为B是老大，B认为C是老大，C认为A是老大，那么，A，B，C都是老大。然后，不要以为这是单纯的并查集，因为，老大这个词不单纯，所以不是单纯的并查集【咳咳，别跑题】然后，我们就可以找到强连通分量，而强连通分量就是通过拓扑图，删掉所有入度为0的节点，直到只剩下一个强连通分量，这就是总的做法。
　　是不是很神奇！
　　才不。
　　so easy！
　　妈妈再也不用担心我的学习【咳咳，又乱入了】
　　好了好了。

　　是时候结束了。

Next Day

Next你ma了ge【哔】
/再见/再见

END.