[算法导论]第八章《线性时间排序》

    本章先回顾了前面介绍的合并排序、堆排序和快速排序的特点及运行运行时间。合并排序和堆排序在最坏情况下达到O(nlgn)，而快速排序最坏情况下达到O(n^2)，平均情况下达到O(nlgn)，因此合并排序和堆排序是渐进最优的。这些排序在执行过程中各元素的次序基于输入元素间的比较，称这种算法为比较排序。接下来介绍了用决策树的概念及如何用决策树确定排序算法时间的下界，最后讨论三种线性时间运行的算法：计数排序、基数排序和桶排序。这些算法在执行过程中不需要比较元素来确定排序的顺序，这些算法都是稳定的。

1、决策树模型

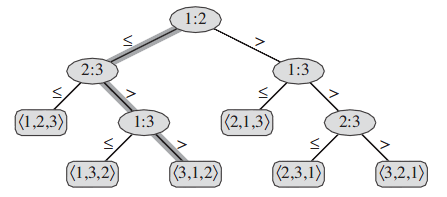
　　 在比较排序算法中，用比较操作来确定输入序列<a1,a2,......,a3>的元素间次序。决策树是一棵完全二叉树，比较排序可以被抽象视为决策树，表示某排序算法作用域给定输入所做的比较。在决策树中，节点表示为i:j，其中1≤i,j≤n，n是待排序元素个数，叶子节点是排序的结果。节点的左子树满足ai≤aj，右子树满足ai>aj。排序算法正确工作的必要条件是：n个元素的n！中排列中的每一种都要作为决策树的一个叶子而出现。举例说明，先有序列A<3,2,1>，对其进行有小到达进行插入排序，排序的决策树如下图所示：

在决策树中，从跟到任意一个可达叶子节点之间最长路径的长度，表示对应的排序算法中最坏情况下的比较次数。

定理:对于一个比较排序算法在最坏情况下，都需要做Ω(nlgn)此比较。

推论：堆排序和合并排序都是渐进最优的比较排序算法。

任何比较的排序在最坏的情况下都要用Ω(nlgn)次比较来进行排序，所以合并排序和堆排序是渐近最优的。 注意的是：快排不是渐近最优的，因为它在最坏的情况下是O(n2)。

2. 三种以线性时间运行的排序算法：计数排序、基数排序和桶排序。它们都是非比较的。

2.1计数排序

a) 计数排序的一个重要性就是它是稳定的排序算法，这个稳定性是基数排序的基石。
b) 计数排序的想法真的很简单、高效、可靠
c) 缺点在于：

i. 需要很多额外的空间（当前类型的值的范围）

ii. 只能对离散的类型有效比如int（double就不行了）

iii. 基于假设：输入是小范围内的整数构成的。

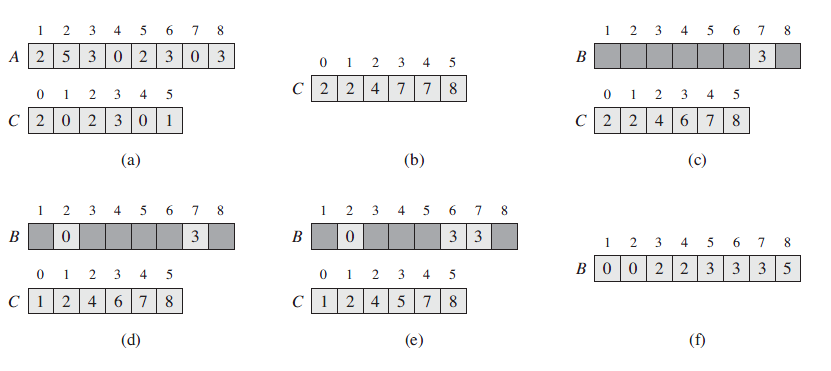
    计数排序假设n个输入元素中的每一个都介于0和k之间的整数，k为n个数中最大的元素。当k=O(n)时，计数排序的运行时间为θ(n)。计数排序的基本思想是：对n个输入元素中每一个元素x，统计出小于等于x的元素个数，根据x的个数可以确定x在输出数组中的最终位置。此过程需要引入两个辅助存放空间，存放结果的B[1...n]，用于确定每个元素个数的数组C[0...k]。算法的具体步骤如下：
（1）根据输入数组A中元素的值确定k的值，并初始化C[1....k]= 0；
（2）遍历输入数组A中的元素，确定每个元素的出现的次数，并将A中第i个元素出现的次数存放在C[A[i]]中，然后C[i]=C[i]+C[i-1]，在C中确定A中每个元素前面有多个元素；
（3）逆序遍历数组A中的元素，在C中查找A中出现的次数，并结果数组B中确定其位置，然后将其在C中对应的次数减少1。
举个例子说明其过程，假设输入数组A=<2,5,3,0,2,3,0,3>，计数排序过程如下：

    书中的伪代码：

COUNTING_SORT(A,B,k)
    for i=0 to k
      do C[i] = 0
    for j=1 to length(A)
        do C[A[j]] = C[A[j]]+1   //C[i]中包含等于元素i的个数
    for i=1 to k
        do C[i] = C[i] + C[i-1]  //C[i]中包含小于等于元素i的个数
    for j=length[A] downto 1
        do B[C[A[j]]] = A[j]
             C[A[j]] = C[A[j]] -1

    代码实现C++：

/*
 *Created by RogerKing
 *Email:jin_tengfei@163.com
 */


#include <iostream>

using namespace std;

int get_K(int A[],int n)
{
	int k=A[0];
	for( int i=1; i<n ; i++ )
	{
		if( k<A[i] )
			k=A[i];
	}
	return k;
}

void Counting_Sort(int A[],int B[], int k,int n)
{
	int* C=new int[k+1];
	int i;
	for( i=0; i<=k ; i++ )
		C[i]=0;
	for( i=0; i<n ; i++ )
		C[A[i]]++;
	for( i=1; i<=k ; i++ )
		C[i]=C[i]+C[i-1];
	for( i=n-1; i>=0 ; i-- )
	{
		B[C[A[i]]-1]=A[i];
		C[A[i]]--;
	}
	delete[] C;
}

void display(int A[],int n)
{
	for( int i=0; i<n ; i++)
		cout<<A[i]<<" ";
	cout<<endl;
}

int main(int argc, char *argv[])
{
	int A[100],B[100];  
    int n;  
    while (cin >> n)  
    {
		for (int i = 0; i < n; i++)  
			cin >> A[i];  
        int k=get_K(A,n);
		Counting_Sort(A,B,k,n);
        display(B, n);  
    }  
	return 0;
}

2.2基数排序

a) 基数排序时对每一维进行调用子排序算法时要求这个子排序算法必须是稳定的。
b) 基数排序与直觉相反：它是按照从底位到高位的顺序排序的。 我觉得原因在于：高有效位对底有效位有着决定性的作用。

基数排序排序过程无须比较关键字，而是通过“分配”和“收集”过程来实现排序，它的时间复杂度可达到线性阶：O(n)。对于十进制数来说，每一位的在[0,9]之中，d位的数，则有d列。基数排序首先按低位有效数字进行排序，然后逐次向上一位进行排序，直到最高位排序结束。举例说明基数排序过程，如下图所示：

    书中的伪代码：

1 RADIX_SORT(A,d）
2    for i=1 to d
3          do usage a stable sort to sort array A on digit i

    代码实现C++：

/*
 *Created by RogerKing
 *Email:jin_tengfei@163.com
 */


#include <iostream>

using namespace std;

int get_K(int A[],int n)
{
	int k=A[0];
	for( int i=1; i<n ; i++ )
	{
		if( k<A[i] )
			k=A[i];
	}
	return k;
}

int get_digit(int n)
{
	int digit=1;
	while( n )
	{
		n/=10;
		digit++;
	}
	return digit;
}

void Radix_Sort(int A[],int n)
{
	int* B=new int[n];
	int C[10];
	int i,j,t,d,radix=1;

	d=get_digit(get_K(A,n));
	for( i=0; i<d ;i++,radix*=10  )
	{
		for( j=0; j<10 ; j++ )
			C[j]=0;
		for( j=0; j<n ; j++ )
		{
			t=A[j]/radix%10;
			C[t]++;
		}
		for( j=1; j<10 ; j++ )
			C[j]=C[j]+C[j-1];
		for( j=n-1; j>=0 ; j-- )
		{
			t=A[j]/radix%10;
			B[C[t]-1]=A[j];
			C[t]--;
		}
		for( j=0; j<n ; j++ )
			A[j]=B[j];
	}
	delete[] B;
}

void display(int A[],int n)
{
	for( int i=0; i<n ; i++)
		cout<<A[i]<<" ";
	cout<<endl;
}

int main(int argc, char *argv[])
{
	int A[100];  
    int n;  
    while (cin >> n)  
    {
		for (int i = 0; i < n; i++)  
			cin >> A[i];  
		Radix_Sort(A,n);
        display(A,n);  
    }  
	return 0;
}

2.3桶排序

a) 桶排序也只是期望运行时间能达到线性，对于最坏的情况，它的运行时间取决于它内部使用的子排序算法的运行时间，一般为O(nlgn)。
b) 桶排序基于假设：输入的的元素均匀的分布在区间[0, 1]上。
c) 感觉桶排没有什么大的实现价值，因为它限定了输入的区间，还要求最好是均匀分布，它的最坏情况并不好。

    计数排序假设输入是由一个小范围内的整数构成，而桶排序则假设输入由一个随机过程产生的，该过程将元素均匀而独立地分布在区间[0，1)上。当桶排序的输入符合均匀分布时，即可以线性期望时间运行。桶排序的思想是：把区间[0，1)划分成n个相同大小的子区间，成为桶（bucket），然后将n个输入数分布到各个桶中去，对各个桶中的数进行排序，然后按照次序把各个桶中的元素列出来即可。

所有的线性时间内的排序算法，都作出了一定的假设，是建立在一定的假设基础上的。