孩子兄弟表示法(二叉链表树)

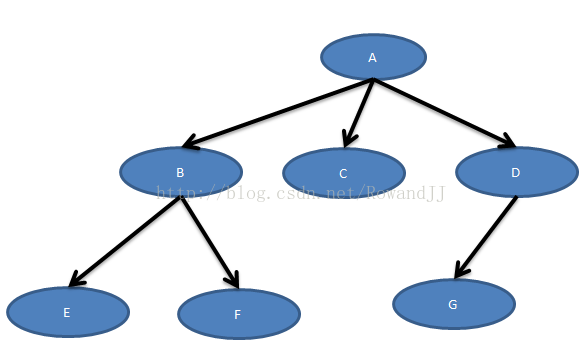
考虑下面这森林：

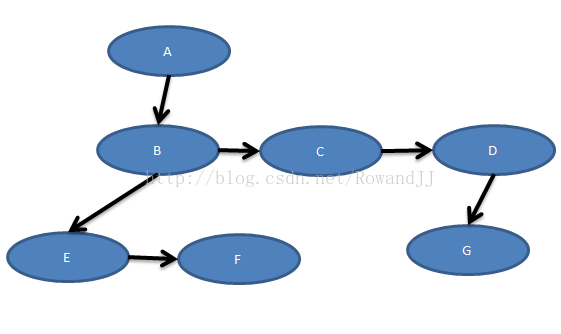
如果用孩子兄弟表示法可以表示为：

顾名思义，孩子兄弟表示法的每个节点有两个指针域，一个指向其长子，另一个指向其兄弟.

实现：

/**************************************************
树的孩子兄弟表示法(二叉链表树)
by Rowandjj
2014/5/25
**************************************************/
#include<iostream>
using namespace std;

typedef char ElemType; 
//--------二叉链表（孩子-兄弟）存储表示-------
typedef struct _TREENODE_
{
    struct _TREENODE_ *pFirstChild;
    struct _TREENODE_ *pNextSibling;
    ElemType data;
}TreeNode,*pTreeNode,**ppTreeNode;

//----------辅助队列-------------------
typedef struct _QUEUENODE_
{
    struct _QUEUENODE_ *pNext;
    pTreeNode data;
}QueueNode,*pQueueNode;

typedef struct _QUEUE_
{
    pQueueNode pHead;
    pQueueNode pTail;
    int nodeCount;
}Queue,*pQueue;

//-----------队列操作定义-----------------------
void InitQueue(pQueue pQueueTemp);
void Enqueue(pQueue pQueueTemp,pTreeNode pTreeNodeTemp);
void Dequeue(pQueue pQueueTemp,ppTreeNode ppTreeNodeTemp);
bool IsQueueEmpty(Queue QueueTemp);
void DestroyQueue(pQueue pQueueTemp);


//------------二叉树操作定义--------------------

void CreateTree(ppTreeNode ppTreeNodeTemp);
void DestroyTree(ppTreeNode ppTreeNodeTemp);
int GetDepth(pTreeNode pTreeNodeTemp);

void PreTravel(pTreeNode pTreeNodeTemp);
void PostTravel(pTreeNode pTreeNodeTemp);
void MidTravel(pTreeNode pTreeNodeTemp);
void LevelTravel(pTreeNode pTreeNodeTemp);

pTreeNode Point(pTreeNode pTreeNodeTemp,ElemType e);
ElemType GetParent(pTreeNode pTreeNodeTemp,ElemType e);

void InsertTree(ppTreeNode ppTreeNodeTemp,ElemType data,int i,pTreeNode pSub);//将psub插入到ppTreeNodeTemp中的值为data的节点的第i个子树
void DeleteTree(ppTreeNode ppTreeNodeTemp,ElemType data,int i);//删除ppTreeNodeTemp中的值为data的节点的第i个子树


//---------队列操作实现---------------
void InitQueue(pQueue pQueueTemp)
{
    pQueueTemp->pHead = pQueueTemp->pTail = (pQueueNode)malloc(sizeof(QueueNode));
    if(pQueueTemp->pHead == NULL)
    {
        return;
    }
    pQueueTemp->nodeCount = 0;
    pQueueTemp->pHead->pNext = NULL;
}
void Enqueue(pQueue pQueueTemp,pTreeNode pTreeNodeTemp)
{
    if(pQueueTemp == NULL)
    {
        return;
    }
    pQueueNode pNew = (pQueueNode)malloc(sizeof(QueueNode));
    if(pNew == NULL)
    {
        return;
    }
    pNew->data = pTreeNodeTemp;
    pNew->pNext = NULL;

    pQueueTemp->pTail->pNext = pNew;
    pQueueTemp->pTail = pNew;
    pQueueTemp->nodeCount++;
}
void Dequeue(pQueue pQueueTemp,ppTreeNode ppTreeNodeTemp)
{
    if(pQueueTemp == NULL)
    {
        return;
    }
    pQueueNode pDel = pQueueTemp->pHead->pNext;
    pQueueTemp->pHead->pNext = pDel->pNext;
    if(pDel == pQueueTemp->pTail)
    {
        pQueueTemp->pTail = pQueueTemp->pHead;
    }
    *ppTreeNodeTemp = pDel->data;
    free(pDel);
    pQueueTemp->nodeCount--;
}
bool IsQueueEmpty(Queue QueueTemp)
{
    return QueueTemp.nodeCount == 0;
}
void DestroyQueue(pQueue pQueueTemp)
{
    if(pQueueTemp != NULL)
    {
        pQueueNode pTravel = pQueueTemp->pHead->pNext;
        while(pTravel != NULL)
        {
            pQueueTemp->pHead->pNext = pTravel->pNext;
            free(pTravel);
            pTravel = pQueueTemp->pHead->pNext;
        }
        free(pQueueTemp->pHead);
        pQueueTemp->nodeCount = 0;
    }
}

//------------二叉树操作实现-------------------------

void CreateTree(ppTreeNode ppTreeNodeTemp)//创建
{
    char szBuffer[20];
    char a;
    cout<<"输入根节点:";
    cin>>a;
    Queue queue;
    InitQueue(&queue);
    if(a != '#')
    {
        *ppTreeNodeTemp = (pTreeNode)malloc(sizeof(TreeNode));
        (*ppTreeNodeTemp)->data = a;
        (*ppTreeNodeTemp)->pNextSibling = NULL;
        Enqueue(&queue,*ppTreeNodeTemp);//入队根节点

        pTreeNode pTemp,pTemp1;
        while(!IsQueueEmpty(queue))
        {
            Dequeue(&queue,&pTemp);
            cout<<"输入"<<pTemp->data<<"的孩子节点:";
            cin>>szBuffer;
            if(szBuffer[0] != '#')
            {
                pTemp->pFirstChild = (pTreeNode)malloc(sizeof(TreeNode));
                
                pTemp->pFirstChild->data = szBuffer[0];
    
                pTemp1 = pTemp->pFirstChild;
                for(int i = 1; i < strlen(szBuffer); i++)
                {
                    pTemp1->pNextSibling = (pTreeNode)malloc(sizeof(TreeNode));
                    Enqueue(&queue,pTemp1);
                    pTemp1->pNextSibling->data = szBuffer[i];
                        
                    pTemp1 = pTemp1->pNextSibling;
                }
                pTemp1->pNextSibling = NULL;
                Enqueue(&queue,pTemp1);

            }else
            {
                pTemp->pFirstChild = NULL;
            }
            
        }

    }else
    {
        *ppTreeNodeTemp = NULL;
    }

}
void DestroyTree(ppTreeNode ppTreeNodeTemp)
{
    if(*ppTreeNodeTemp != NULL)
    {
        if((*ppTreeNodeTemp)->pFirstChild != NULL)
        {
            DestroyTree(&(*ppTreeNodeTemp)->pFirstChild);    
        }
        if((*ppTreeNodeTemp)->pNextSibling != NULL)
        {
            DestroyTree(&(*ppTreeNodeTemp)->pNextSibling);
        }
        free(*ppTreeNodeTemp);
        *ppTreeNodeTemp = NULL;
    }
}


int GetDepth(pTreeNode pTreeNodeTemp)
{
    if(pTreeNodeTemp == NULL)
    {
        return 0;
    }
    if(pTreeNodeTemp->pFirstChild == NULL)
    {
        return 1;
    }
    int depth,max = 0;
    pTreeNode pTemp = pTreeNodeTemp->pFirstChild;
    for(;pTemp != NULL; pTemp = pTemp->pNextSibling)
    {
        depth = GetDepth(pTemp);
        if(depth > max)
        {
            max = depth;
        }
    }
    return max+1;
}

void PreTravel(pTreeNode pTreeNodeTemp)
{
    if(pTreeNodeTemp)
    {
        cout<<pTreeNodeTemp->data<<" ";
        PreTravel(pTreeNodeTemp->pFirstChild);
        PreTravel(pTreeNodeTemp->pNextSibling);
    }
}

void MidTravel(pTreeNode pTreeNodeTemp)
{
    if(pTreeNodeTemp)
    {
        MidTravel(pTreeNodeTemp->pFirstChild);
        cout<<pTreeNodeTemp->data<<" ";
        MidTravel(pTreeNodeTemp->pNextSibling);
    }
}


void PostTravel(pTreeNode pTreeNodeTemp)
{
    if(pTreeNodeTemp)
    {
        PostTravel(pTreeNodeTemp->pFirstChild);
        PostTravel(pTreeNodeTemp->pNextSibling);
        cout<<pTreeNodeTemp->data<<" ";
    }
}

pTreeNode Point(pTreeNode pTreeNodeTemp,ElemType e)
{
    Queue queue;
    InitQueue(&queue);
    if(pTreeNodeTemp != NULL)
    {
        Enqueue(&queue,pTreeNodeTemp);

        pTreeNode pTemp;
        while(!IsQueueEmpty(queue))
        {
            Dequeue(&queue,&pTemp);
            if(pTemp->data == e)
            {
                DestroyQueue(&queue);
                return pTemp;
            }else
            {
                pTreeNode pSibling = NULL;
                if(pTemp->pFirstChild != NULL)
                {
                    Enqueue(&queue,pTemp->pFirstChild);//入队长子
                     pSibling = pTemp->pFirstChild->pNextSibling;
                }
                 
                while(pSibling != NULL)
                {
                    Enqueue(&queue,pSibling);//入队兄弟
                    pSibling = pSibling->pNextSibling;
                }
            }
        }

    }
    return NULL;
}

ElemType GetParent(pTreeNode pTreeNodeTemp,ElemType e)
{
    Queue queue;
    InitQueue(&queue);
    
    if(pTreeNodeTemp != NULL)
    {
        if(pTreeNodeTemp->data == e)
        {
            return -1;
        }
        Enqueue(&queue,pTreeNodeTemp);

        pTreeNode pTemp,pTemp1;
        while(!IsQueueEmpty(queue))
        {
            Dequeue(&queue,&pTemp);
            if(pTemp->pFirstChild)
            {
                if(pTemp->pFirstChild->data == e)
                {
                    return pTemp->data;
                }
                pTemp1 = pTemp;
                
                Enqueue(&queue,pTemp->pFirstChild);//入队长子
                pTemp = pTemp->pFirstChild;

                while(pTemp->pNextSibling)
                {
                    pTemp = pTemp->pNextSibling;
                    if(pTemp->data == e)
                    {
                        return pTemp1->data;
                    }
                    Enqueue(&queue,pTemp);//入队兄弟
                }
            }
        }
    }

    return -1;
}

void LevelTravel(pTreeNode pTreeNodeTemp)//层次遍历
{
    Queue queue;
    InitQueue(&queue);

    if(pTreeNodeTemp != NULL)
    {
        cout<<pTreeNodeTemp->data<<" ";
        Enqueue(&queue,pTreeNodeTemp);
        
        pTreeNode pTemp;
        while(!IsQueueEmpty(queue))
        {
            Dequeue(&queue,&pTemp);
            
            if(pTemp->pFirstChild != NULL)
            {
                pTemp = pTemp->pFirstChild;
                cout<<pTemp->data<<" ";
                Enqueue(&queue,pTemp);//入队长子
                while(pTemp->pNextSibling != NULL)
                {
                    pTemp = pTemp->pNextSibling;
                    cout<<pTemp->data<<" ";
                    Enqueue(&queue,pTemp);
                }
            }

        }    
    }
}

void InsertTree(ppTreeNode ppTreeNodeTemp,ElemType data,int i,pTreeNode pSub)
{
    if(*ppTreeNodeTemp == NULL)
    {
        return;
    }

    pTreeNode pTreeNodeTemp = Point(*ppTreeNodeTemp,data);
    if(pTreeNodeTemp != NULL)
    {
        if(i==1)
        {
            pSub->pNextSibling = pTreeNodeTemp->pFirstChild;
            pTreeNodeTemp->pFirstChild = pSub;
        }else
        {
            int j = 2;
            pTreeNodeTemp = pTreeNodeTemp->pFirstChild;
            while (j < i && pTreeNodeTemp)
            {
                pTreeNodeTemp = pTreeNodeTemp->pNextSibling;
                j++;
            }
            if(j == i)
            {
                pSub->pNextSibling = pTreeNodeTemp->pNextSibling;
                pTreeNodeTemp->pNextSibling = pSub;
            }else
            {
                return;
            }
        }
    }
}

void DeleteTree(ppTreeNode ppTreeNodeTemp,ElemType data,int i)
{
    if(*ppTreeNodeTemp == NULL)
    {
        return;
    }
    pTreeNode pTemp;
    pTreeNode pTreeNodeTemp = Point(*ppTreeNodeTemp,data);
    if(pTreeNodeTemp != NULL)
    {    
        if(i == 1)//删除长子
        {
            pTemp = pTreeNodeTemp->pFirstChild;
            pTreeNodeTemp->pFirstChild = pTemp->pNextSibling;
            pTemp->pNextSibling = NULL;
            DestroyTree(&pTemp);
        }else
        {
            pTreeNodeTemp = pTreeNodeTemp->pFirstChild;
            int j = 2;
            while(j < i && pTreeNodeTemp)
            {
                pTreeNodeTemp = pTreeNodeTemp->pNextSibling;    
                j++;
            }

            if(j == i)
            {
                pTemp = pTreeNodeTemp->pNextSibling;
                pTreeNodeTemp->pNextSibling = pTemp->pNextSibling;
                pTemp->pNextSibling = NULL;
                DestroyTree(&pTemp);
            }
        }
    }
}