十字链表是有向图的另一种链式存储结构。可以看成是将有向图的邻接表和逆邻接表(只考虑入度)结合起来得到的一种链表。在十字链表中,对应于有向图中每一个顶点有一个节点,每一条弧也有一个结点。
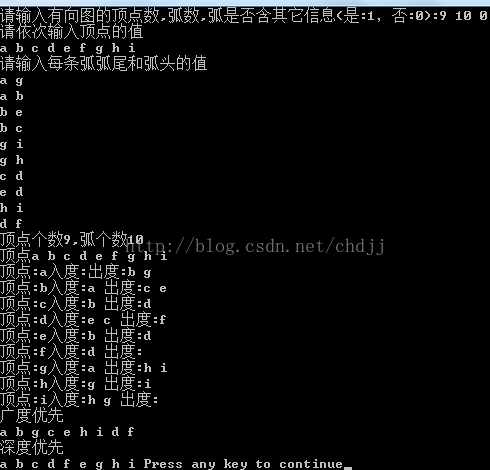
测试:
顶点之间是数组顺序存储,而弧是链式存储。
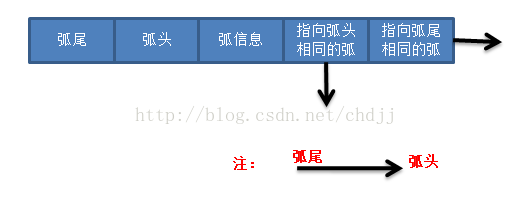
弧结点结构:
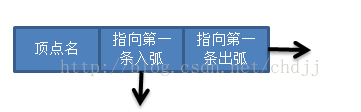
顶点结点结构:

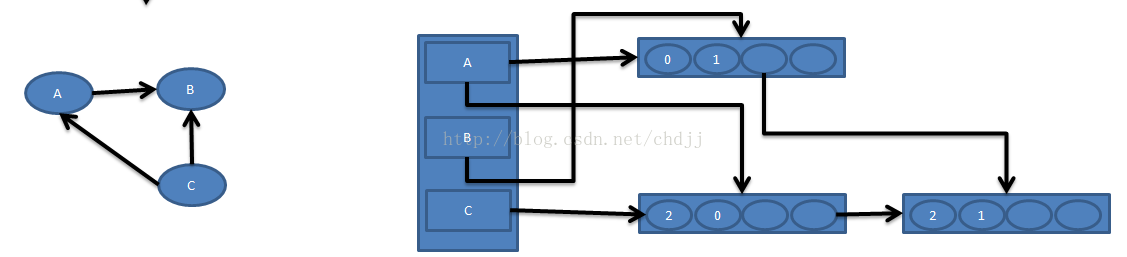
十字链表形态:
实现:
/***********************************************
有向图的存储形式——十字链表
by Rowandjj
2014/6/27
***********************************************/
#include<IOSTREAM>
using namespace std;
#define MAX_VERTEX_NUM 20//顶点最大长度
#define MAX_INFO 20//弧信息的最大长度
typedef struct _ARCBOX_//弧结点
{
int tailvex,headvex;//该弧的尾和头顶点的位置
struct _ARCBOX_ *hlink,*tlink;//分别为弧头相同和弧尾相同的弧的链域
char *info;
}ArcBox;
typedef struct _VEXNODE_//顶点
{
char data;//顶点名称
ArcBox *firstin,*firstout;
}VexNode;
typedef struct _OLGRAPH_//图
{
VexNode xlist[MAX_VERTEX_NUM];//表头向量(数组)
int vexnum,arcnum;//顶点数目,弧数目
}OLGraph;
//------------------操作定义---------------------------------
int LocateVex(OLGraph G,char u);//返回顶点u在有向图G中的位置(序号),如不存在则返回-1
bool CreateDG(OLGraph* G);//采用十字链表存储表示,构造有向图G
void Display(OLGraph G);//输出有向图G
void DestroyGraph(OLGraph* G);//销毁有向图G
char GetVex(OLGraph G,int v);//返回v的值
bool PutVex(OLGraph* G,char v,char value);//对v赋新值value
int FirstAdjVex(OLGraph G,char v);//返回v的第一个邻接顶点的序号。若顶点在G中没有邻接顶点,则返回-1
int NextAdjVex(OLGraph G,char v,char w);//返回v的(相对于w的)下一个邻接顶点的序号,若w是v的最后一个邻接顶点,则返回-1
void InsertVex(OLGraph* G,char v);//在有向图G中增添新顶点v(不增添与顶点相关的弧,留待InsertArc()去做)
bool DeleteVex(OLGraph* G,char v);//删除G中顶点v及其相关的弧
bool InsertArc(OLGraph* G,char v,char w);//在G中增添弧<v,w>
bool DeleteArc(OLGraph* G,char v,char w);//在G中删除弧<v,w>
void DFSTravel(OLGraph G,void (*Visit)(char));
void DFS(OLGraph G,int v);
void BFSTravel(OLGraph G,void (*Visit)(char));
void (*VisitFunc)(char); //全局函数指针
bool visited[MAX_VERTEX_NUM]; /* 访问标志数组(全局量) */
//-----------------------------------------------------------
void Visit(char p)
{
cout<<p<<" ";
}
//辅助队列
typedef struct _QUEUENODE_
{
int data;
struct _QUEUENODE_ *next;
}QueueNode;
typedef struct _QUEUE_
{
QueueNode *pHead;
QueueNode *pTail;
int size;
}Queue;
bool InitQueue(Queue *Q);
bool DestroyQueue(Queue *Q);
bool DeQueue(Queue *Q,int* e);
bool EnQueue(Queue *Q, int e);
bool QueueEmpty(Queue Q);
//-----------------------------------------------------------
bool InitQueue(Queue *Q)
{
Q->pHead = Q->pTail = (QueueNode*)malloc(sizeof(QueueNode));
if(!Q->pHead)
{
return false;
}
Q->pHead->next = NULL;
Q->size = 0;
return true;
}
bool EnQueue(Queue *Q, int e)
{
QueueNode *newNode = (QueueNode *)malloc(sizeof(QueueNode));
if(!newNode)
{
return false;
}
newNode->data = e;
newNode->next = NULL;
Q->pTail->next = newNode;
Q->pTail = newNode;
Q->size++;
return true;
}
bool DeQueue(Queue *Q,int* e)
{
QueueNode *pDel = Q->pHead->next;
if(!pDel)
{
return false;
}
*e = pDel->data;
if(Q->pTail == pDel)
{
Q->pTail = Q->pHead;
}
Q->pHead->next = pDel->next;
free(pDel);
Q->size--;
return true;
}
bool QueueEmpty(Queue Q)
{
return Q.size == 0;
}
bool DestroyQueue(Queue *Q)
{
QueueNode *p,*q;
p = Q->pHead->next;
while(p)
{
q = p->next;
free(p);
p = q;
}
free(Q->pHead);
Q->pHead = NULL;
Q->size = 0;
return true;
}
//-----------------------------------------------------------
int LocateVex(OLGraph G,char u)
{
int i;
for(i = 0; i < G.vexnum; i++)//用循环查找该结点
{
if(u == G.xlist[i].data)
{
return i;
}
}
return -1;
}
bool CreateDG(OLGraph* G)
{
int i,j,k;
int IncInfo;//弧是否包含其他信息
ArcBox *pArc;
char v1,v2;//弧尾、弧头
char str[MAX_INFO];//弧的相关信息
cout<<"请输入有向图的顶点数,弧数,弧是否含其它信息(是:1,否:0):";
cin>>G->vexnum;
cin>>G->arcnum;
cin>>IncInfo;
cout<<"请依次输入顶点的值"<<endl;
for(i = 0; i < G->vexnum; i++)
{
cin>>G->xlist[i].data;
G->xlist[i].firstin = NULL;
G->xlist[i].firstout = NULL;
}
cout<<"请输入每条弧弧尾和弧头的值"<<endl;
for(k = 0; k < G->arcnum; k++)//输入各弧并构造十字链表
{
//注意:如果i------>j 则代表i为弧尾,或者起始点。j代表弧头,又叫终端点
cin>>v1;//输入弧尾(起始点)
cin>>v2;//输入弧头(终端点)
pArc = (ArcBox *)malloc(sizeof(ArcBox));
//得到弧尾和弧头的位置
i = LocateVex(*G,v1);//弧尾的位置
j = LocateVex(*G,v2);//弧头的位置
if(i == -1 || j == -1)
{
return false;
}
pArc->tailvex = i;
pArc->headvex = j;
pArc->tlink = G->xlist[i].firstout;
pArc->hlink = G->xlist[j].firstin;
G->xlist[i].firstout = pArc;
G->xlist[j].firstin = pArc;
if(IncInfo)
{
cout<<"输入弧的相关信息:"<<endl;
cin>>str;
pArc->info = (char *)malloc(sizeof(char)*(strlen(str)+1));
strcpy(pArc->info,str);
}else
{
pArc->info = NULL;
}
}
return true;
}
void Display(OLGraph G)
{
int i;
ArcBox *pArc;
cout<<"顶点个数"<<G.vexnum<<",弧个数"<<G.arcnum<<endl;
cout<<"顶点";
for(i = 0; i < G.vexnum; i++)
{
cout<<G.xlist[i].data<<" ";
}
cout<<endl;
for(i = 0; i < G.vexnum; i++)
{
cout<<"顶点:"<<G.xlist[i].data<<"入度:";//弧头相同
pArc = G.xlist[i].firstin;
while(pArc)
{
cout<<G.xlist[pArc->tailvex].data<<" ";
pArc = pArc->hlink;
}
cout<<"出度:";
pArc = G.xlist[i].firstout;
while(pArc)
{
cout<<G.xlist[pArc->headvex].data<<" ";
if(pArc->info)
{
cout<<pArc->info<<" ";
}
pArc = pArc->tlink;
}
cout<<endl;
}
}
void DestroyGraph(OLGraph* G)
{
int i;
ArcBox *pArc1,*pArc2;
for(i = 0 ; i < G->vexnum; i++)
{
pArc1 = G->xlist[i].firstout;
while(pArc1)
{
pArc2 = pArc1->tlink;
if(pArc1->info)
{
free(pArc1->info);
}
free(pArc1);
pArc1 = pArc2;
}
}
}
char GetVex(OLGraph G,int v)
{
if(v < 0 || v >= G.vexnum)
{
exit(0);
}
return G.xlist[v].data;
}
bool PutVex(OLGraph* G,char v,char value)
{
int i = LocateVex(*G,v);
if(i < 0)
{
return false;
}
G->xlist[i].data = value;
return true;
}
int FirstAdjVex(OLGraph G,char v)
{
int i;
i = LocateVex(G,v);
ArcBox *p = G.xlist[i].firstout;
if(p)
{
return p->headvex;
}else
{
return -1;
}
}
int NextAdjVex(OLGraph G,char v,char w)
{
int i,j;
ArcBox *pArc;
i = LocateVex(G,v);
j = LocateVex(G,w);
pArc = G.xlist[i].firstout;
while(pArc && pArc->headvex!=j)
{
pArc = pArc->tlink;
}
if(pArc)
{
pArc = pArc->tlink;
}
if(pArc)
{
return pArc->headvex;
}else
{
return -1;
}
}
void InsertVex(OLGraph* G,char v)
{
G->xlist[G->vexnum].data = v;
G->xlist[G->vexnum].firstin = G->xlist[G->vexnum].firstout = NULL;
G->vexnum++;
}
bool DeleteVex(OLGraph* G,char v)
{
int j,k;
ArcBox *p,*q;
k = LocateVex(*G,v);
if(k < 0)
{
return false;
}
//1.删除v的出弧
//1.1v的出弧也就是其他顶点的入弧,我们需要在其他弧的入弧链表中删除v的出弧
for(j = 0; j < G->vexnum; j++)
{
if(j == k)
{
continue;
}
p = G->xlist[j].firstin;
while(p)
{
if(k == p->tailvex && p == G->xlist[j].firstin)//如果待删结点为首结点
{
G->xlist[j].firstin = p->hlink;
break;
}else if(k != p->tailvex)//当前结点不是待删结点
{
q = p;
p = p->hlink;
}else//待删结点不是首节点
{
q->hlink = p->hlink;
break;
}
}
}
//1.2删除v的出弧
p = G->xlist[k].firstout;
while(p)
{
q = p->tlink;
if(p->info)
{
free(p->info);
}
free(p);
G->arcnum--;
p = q;
}
//2.删除顶点v的入弧
//2.1顶点v的入弧也就是其他顶点的出弧,我们需要在其他弧的出弧链表中删除v的入弧
for(j = 0; j < G->vexnum; j++)
{
if(j == k)
{
continue;
}
p = G->xlist[j].firstout;
while(p)
{
if(k == p->headvex && p == G->xlist[j].firstout)
{
G->xlist[j].firstout = p->tlink;
break;
}else if(k != p->headvex)
{
q = p;
p = p->tlink;
}else
{
q->tlink = p->tlink;
break;
}
}
}
//2.2删除顶点v的入弧
p = G->xlist[k].firstin;
while(p)
{
q = p->hlink;
if(p->info)
{
free(p->info);
}
free(p);
p = q;
G->arcnum--;
}
//3.序号>k的顶点依次向前移
for(j = k+1; j < G->vexnum; j++)
{
G->xlist[j-1] = G->xlist[j];
}
G->vexnum--;
//4.结点序号>k的要减1
for(j = 0; j < G->vexnum; j++)
{
p = G->xlist[j].firstout;
while(p)
{
if(p->headvex > k)
{
p->headvex--;
}
if(p->tailvex > k)
{
p->tailvex--;
}
p = p->tlink;
}
}
return true;
}
bool InsertArc(OLGraph* G,char v,char w)
{
int IncInfo;
char str[MAX_INFO];
int i,j;
ArcBox *pArc;
i = LocateVex(*G,v);//弧尾
j = LocateVex(*G,w);//弧头
if(i < 0 || j < 0)
{
return false;
}
pArc = (ArcBox *)malloc(sizeof(ArcBox));
pArc->tailvex = i;
pArc->headvex = j;
pArc->tlink = G->xlist[i].firstout;
pArc->hlink = G->xlist[j].firstin;
G->xlist[i].firstout = pArc;
G->xlist[j].firstin = pArc;
G->arcnum++;
cout<<"要插入的弧是否含有其它信息(是: 1,否: 0):";
cin>>IncInfo;
if(IncInfo)
{
cout<<"输入弧信息:";
cin>>str;
pArc->info = (char *)malloc(sizeof(char)*(strlen(str)+1));
strcpy(pArc->info,str);
}else
{
pArc->info = NULL;
}
return true;
}
bool DeleteArc(OLGraph* G,char v,char w)
{
int i,j;
ArcBox *p,*q;
i = LocateVex(*G,v);
j = LocateVex(*G,w);
if(i < 0 || j < 0)
{
return false;
}
//先删除顶点v出弧
p = G->xlist[i].firstout;
if(p && p->headvex == j)//待删结点为首节点
{
G->xlist[i].firstout = p->tlink;
}
else
{
while(p && p->headvex != j)
{
q = p;
p = p->tlink;
}
if(p)
{
q->tlink = p->tlink;
}
}
//删除顶点w的入弧
p = G->xlist[j].firstin;
if(p && p->tailvex == i)
{
G->xlist[j].firstin = p->hlink;
}else
{
while(p && p->tailvex != i)
{
q = p;
p = p->hlink;
}
if(p)
{
q->hlink = p->hlink;
}
}
if(p->info)
{
free(p->info);
}
G->arcnum--;
return true;
}
void DFS(OLGraph G,int v)
{
int i;
char v1,w1;
v1 = GetVex(G,v);
visited[v] = true;
VisitFunc(v1);
for(i = FirstAdjVex(G,v1);i>=0;i = NextAdjVex(G,v1,w1 = GetVex(G,i)))
{
if(!visited[i])
{
DFS(G,i);
}
}
}
void DFSTravel(OLGraph G,void (*Visit)(char))
{
int i;
for(i = 0; i < G.vexnum; i++)
{
visited[i] = false;
}
VisitFunc = Visit;
for(i = 0; i < G.vexnum; i++)
{
if(!visited[i])
{
DFS(G,i);
}
}
}
void BFSTravel(OLGraph G,void (*Visit)(char))
{
int i,u,w;
char u1,w1;
Queue queue;
InitQueue(&queue);
for(i = 0; i < G.vexnum; i++)
{
visited[i] = false;
}
for(i = 0; i < G.vexnum; i++)
{
if(!visited[i])
{
visited[i] = true;
Visit(G.xlist[i].data);
EnQueue(&queue,i);
while(!QueueEmpty(queue))
{
DeQueue(&queue,&u);
u1 = GetVex(G,u);
for(w = FirstAdjVex(G,u1);w>=0;w = NextAdjVex(G,u1,w1=GetVex(G,w)))
{
if(!visited[w])
{
visited[w] = true;
Visit(G.xlist[w].data);
EnQueue(&queue,w);
}
}
}
}
}
}
int main()
{
OLGraph graph;
CreateDG(&graph);
Display(graph);
cout<<"广度优先"<<endl;
BFSTravel(graph,Visit);
cout<<"\n深度优先"<<endl;
DFSTravel(graph,Visit);
return 0;
}
测试:










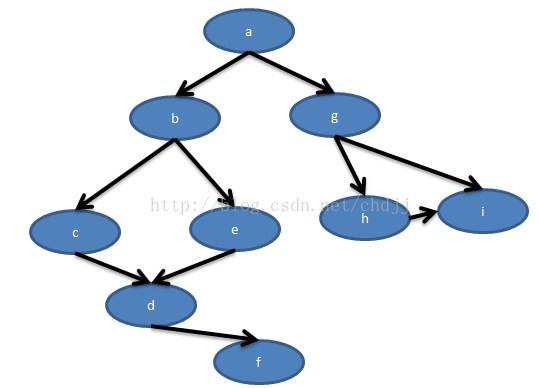
















 4900
4900

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








