数据结构复习六：图

图的存储结构

邻接矩阵

邻接矩阵是表示顶点之间相邻关系的矩阵。

无向图中两点有边相连为1，否则为0；

有向图中vi指向vj则记为wij，否则记为无穷

优点：便于判断两个顶点间是否有边；便于计算顶点的度（无向图：行为度；有向图：行为出度，列为入度）

缺点：不便于增删顶点；不便于统计边的数目；空间复杂度高；

邻接表

邻接表是图的一种链式存储结构。

在邻接表中，对图中每一个顶点vi建立一个单链表，把与vi相邻的顶点放在这个链表中；

优点：便于增删顶点；便于统计边的数目；空间效率高；

缺点：不便于判断顶点之间是否有边；不便于计算有向图各个顶点的度；

十字链表

十字链表可以看成是将有向图的邻接表和逆邻接表结合起来得到的一种链表。其中对应于每一条弧有一个结点，对应于每一个顶点也有一个结点。适用于有向图。

弧结点

tailvex

headvex

hlink

tlink

info

顶点结点

data

firstin

firstout

弧结点中：尾域（tailvex）和头域（headvex）分别指示弧尾和弧头这两个顶点在图中的位置，链域hlink指向弧头相同的下一条弧，info域指向该弧的相关信息。弧头相同的弧在同一链表上，弧尾相同的弧也在同一链表上。

它们的头结点即为顶点结点，其中data域存储和顶点相关的信息，如顶点名称等；firstin和firstout为两个链域，分别指向以该顶点为弧头或弧尾的第一个弧结点。

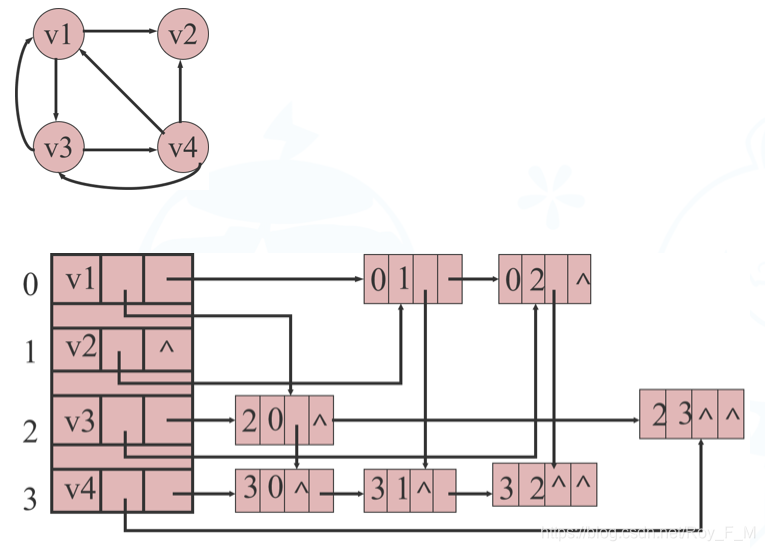
邻接多重表

邻接多重表的结构和十字链表的结构类似，适用于无向图。

边结点

mark

ivex

ilink

jvex

jlink

info

顶点结点

data

firstedge

边结点中，mark为标志域，用以标记该条边是否被搜索过；ivex和jvex为该边依附的两个顶点在图中的位置；ilink指向下一条依附于顶点ivex的边；jlink指向下一条依附于顶点jvex的边，info为指向和边相关的各种信息的指针域

顶点结点中，data域存储和该顶点相关边的信息，firstedge域指示第一条依附于该顶点的边。

图的遍历

图的遍历是从图中某一顶点出发，按照某种方法对图中所有顶点访问且仅访问一次。

深度优先搜索（DFS）

深度优先搜索遍历的过程如下：

1、从图中某个顶点v出发，访问v

2、找出刚访问过的顶点的第一个未被访问的邻接点，访问该顶点。以该顶点为新顶点，重复此步骤，直至刚访问过的顶点没有被访问过的邻接点为止

3、返回前一个访问过的且仍有未被访问的邻接点的顶点，找出该顶点的下一个未被访问的邻接点，访问该顶点

4、重复步骤2和3，直至图中所有顶点都被访问过，搜索结束。

算法步骤：

1、从图中某个顶点v出发，访问v，并置visited[v]的值为true

2、依次检查v所有邻接点w，如果visited[w]的值为false，再从w出发进行递归遍历，直到图中所有顶点都被访问过

算法实现（连通图，邻接矩阵实现）：

bool visited[MVNum];//初始化为false
void DFS(Graph G,int V){
    cout<<v;
    visited[v]=true;
    for(w=0;w<G.vexnum;w++)
    if(G.arcs[v][w]!=0&&!visited[w]) DFS(G,w);
}

算法实现（非连通图）

void DFSTraverse(Graph G){
    for(v=0;v<G.vexnum;++v)visited[v]=false;
    for(v=0;v<G.vexnum;++v)
    if(!visited[v]) DFS(G,v);
}

时间复杂度：邻接矩阵：O(n^2)；邻接表：O(n+e)。

广度优先搜索（BFS）

广度优先搜索遍历的过程如下：

1、从图中某个顶点v出发，访问v

2、依次访问v的各个未曾访问过的邻接点

3、分别从这些邻接点出发依次访问它们的邻接点，并使“先被访问的顶点的邻接点”先于“后被访问的顶点的邻接点”被访问。重复步骤3，直至图中所有已被访问的顶点的邻接点都被访问到。

算法步骤：

1、从图中某个顶点v出发，访问v，并置visited[v]为true，然后将v进队

2、只要队列不空，则重复以下操作：

（1）队头顶点u出队；

（2）依次检查u的所有邻接点w，如果visited[w]的值为false，则访问w，并置visited[w]的值为true，然后将w进队。

算法实现（邻接矩阵）：

void BFS(Graph G,int v){
    cout<<v;
    visited[v]=true;
    initQueue(Q);
    EnQueue(Q,v);
    while(!QueueEmpty(Q)){
        DeQueue(Q,u);
        for(w=0;w<G.vexnum;w++){
            if(G.arcs[u][w]!=0&&!visited[w]){
                cout<<w;
                visited[w]=true;
                EnQueue(Q,w);
            }
        }
    }
}

 

时间复杂度：邻接矩阵：O(n^2)；邻接表：O(n+e)

图的应用

最小生成树

Prim算法

寻找已选点U集与未选点V集最近的点，记为u0，v0，将v0加入U集中，同时将u0记为v0的邻接点，记下此时最小花费

值为0的是已加入U集的点

v1	v2	v3	v4	v5	v6
0	6	1	5	INF	INF	(v1,v3),cost=1
0	5	0	5	6	4	(v3,v6),cost=4
0	5	0	2	6	0	(v6,v4),cost=2
0	5	0	0	6	0	(v3,v2),cost=5
0	0	0	0	3	0	(v2,v5),cost=3
0	0	0	0	0	0	结束

代码：

struct edge{
    int adjvex;        //连接的顶点
    int lowcost;
}closedge[maxn];
int Min_edge(edge e[],int n){
    int min_edge=INF,min_ans;
    for(int i=1;i<=n;++i){
        if(e[i].lowcost<min_edge&&e[i].lowcost!=0){
            min_edge=e[i].lowcost;
            min_ans=i;
        }
    }
    return min_ans;
}
void MiniSpanTree_Prim(AMGraph G,int u){
    for(int j=1;j<=G.vexnum;++j){
        if(j!=u) closedge[j]={u,G.arcs[u][j]};//初始化
    }
        closedge[u].lowcost=0;          //初始 U={u}
        for(int i=1;i<G.vexnum;++i){
            int x=Min_edge(closedge,G.vexnum);     
            int u0=closedge[x].adjvex;
            int v0=x;
            cout<<"<v"<<u0<<",v"<<v0<<">\n";
            closedge[x].lowcost=0;          //第x个顶点并入U集
            for(int j=1;j<=G.vexnum;++j){           //新顶点并入U后，重新选择最小边,更新lowcost
                if(G.arcs[x][j]<closedge[j].lowcost)
                    closedge[j]={x,G.arcs[x][j]};
            }
        }
}

适用于稠密图，时间复杂度为O(n^2)。

Kruskal算法

将边按权值由小到大排序，按顺序选择边加入无边非连通图T中，若在T中不形成回路则加入，否则选择下一边，直至T中所有顶点都在同一连通分量中；

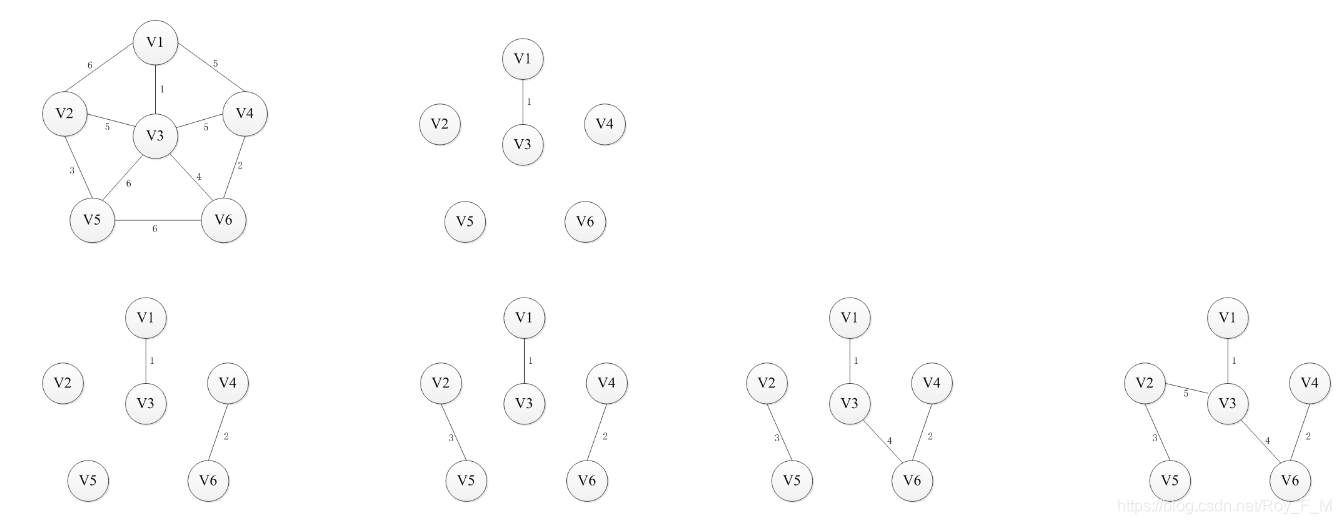
代码：

void MiniSpanTree_Kruskal(AMGraph &G){
    sort(Edge+1,Edge+G.vexnum*2,cmp);
    int Vexset[maxn];
    for(int i=1;i<=G.vexnum;++i){
        Vexset[i]=i;
    }
    int k=1;
    for(int i=1;i<=G.vexnum;++i){
        int v1=Edge[k].head;
        int v2=Edge[k].tail;
        int vs1=Vexset[v1];
        int vs2=Vexset[v2];
        if(vs1!=vs2){
            cout<<"<v"<<Edge[k].head<<",v"<<Edge[k].tail<<">\n";
            for(int j=1;j<=G.vexnum;++j){
                if(Vexset[j]==vs2)
                    Vexset[j]=vs1;
            }
        }
        k=k+2;
    }
}

最短路径

Dijkstra算法

将顶点分为两组：

S：已求出最短路径的点的集合，初始只有v0

V-S：待求出最短路径的顶点的集合，初始为V-{v0}

算法将按各顶点与v0间最短路径长度递增的次序，逐个将集合V-S中的顶点加入到S中

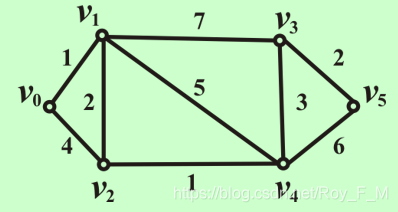
如上图，每行为当前最短路径（直接从v0到达，或经过S中其他点中转到达），取出最小的加入S中，再更新剩余点的最短距离，直至S=V

代码：

void dij(int s){
    int minn;//临时保存当前的最短距离
    dis[s]=0;
    for(int i=1;i<=n;i++){//选出权值最小的点
        int ui=-1;//即将加入s集合的顶点的编号
        minn=MAX_INT;
        for(int j=1;j<=n;j++){
            if(!vis[j]&&dis[j]<minn){
                minn=dis[j];
                ui=j;
            }
        }
        if(ui==-1) break;
        vis[ui]=1;
        for(int j=1;j<=n;j++){//更新距离
            if(!vis[j]&&dis[j]>dis[ui]+graph[ui][j])
            {
                dis[j]=dis[ui]+graph[ui][j];
                dist[s][j]=dis[j];
            }
        }
    }
    return;
}

Floyd算法

比较简单粗暴的算法，所求结果是各个点之间的最短路

直接上代码：

void Floyd(){
    for(int k=1;k<=n;k++){
        for(int i=1;i<=n;i++){
            for(int j=1;j<=n;j++){
                if(dist[i][k]+dist[k][j]<dist[i][j]){
                    dist[i][j]=dist[i][k]+dist[k][j];
                }
            }
        }
    }
}

拓扑排序

AOV-网：用顶点表示活动，用弧表示活动的优先关系的有向图；包含某个或某些活动是其他某个或某些活动的先决条件的信息

拓扑排序就是将AOV-网中所有顶点排成一个线性序列，该序列满足：若在AOV-网中由顶点vi到vj有一条路径，则在该线性序列中的顶点vi必定在vj之前；

算法实现过程：

（删入度为0的点及其所射出的弧，重复此操作）

算法步骤：

1、求出各顶点的入读存入数组indegree[]中，把入读为0的顶点入栈

2、只要栈不空，则重复以下操作：

（1）将栈顶顶点vi出栈并保存在拓扑序列数组topo中

（2）对顶点vi的每个邻接点vk的入度减1，如果vk入度变为0，vk入栈；

3、如果输出顶点个数少于网中顶点个数，则网中存在有向环，无法进行拓扑排序，否则拓扑排序成功。

时间复杂度：O(n+e)。

关键路径

AOE-网：与AOV-网相对，是以边表示活动的网。

 

————————————————————————————————————————————————————————

图片来源：https://www.cnblogs.com/wkfvawl/p/9985083.html

https://www.cnblogs.com/lbrs/p/11879357.html

https://blog.csdn.net/qq_41713256/article/details/80805338

注：本文所有内容均来源于《数据结构（C语言第二版）》（严蔚敏老师著）