线段树专题

最新推荐文章于 2021-07-10 09:51:05 发布

Royecode

最新推荐文章于 2021-07-10 09:51:05 发布

阅读量826

点赞数

分类专栏： Study 文章标签：线段树区间查询区间更新

本文链接：https://blog.csdn.net/Royecode/article/details/46917483

版权

Study 专栏收录该内容

8 篇文章 0 订阅

订阅专栏

引入：

有一个数组arr[1]…..arr[n]，共n个元素，现在有q次操作，操作有两种类型：

1.询问[L,R]区间的和（或极值）
2.将区间[L,R]的每个元素加上val

如有arr[] = {1, 2, 3, 4, 5}（下标从1开始），区间[2, 3]的和等于5，将区间[1, 3]每个元素加1，数组就变成了arr[] = {2, 3, 4, 4 , 5}。
若用朴素的方法，直接在arr[]数组上扫描区间求值，或者修改。时间复杂度：每次询问区间的和（或极值）的时间复杂度是 $O(n)$ ；每次将区间加上一个val时间复杂度是 $O(n)$ 。共q次操作，所以总的时间复杂度 $O(nq)$ ，当n = q = 10w时，这钟做法就显得非常非常低效。
现在有一种树能将实现上述的功能，并且将时间复杂度降为 $O(nlogn)$ ，这种树就叫做线段树。
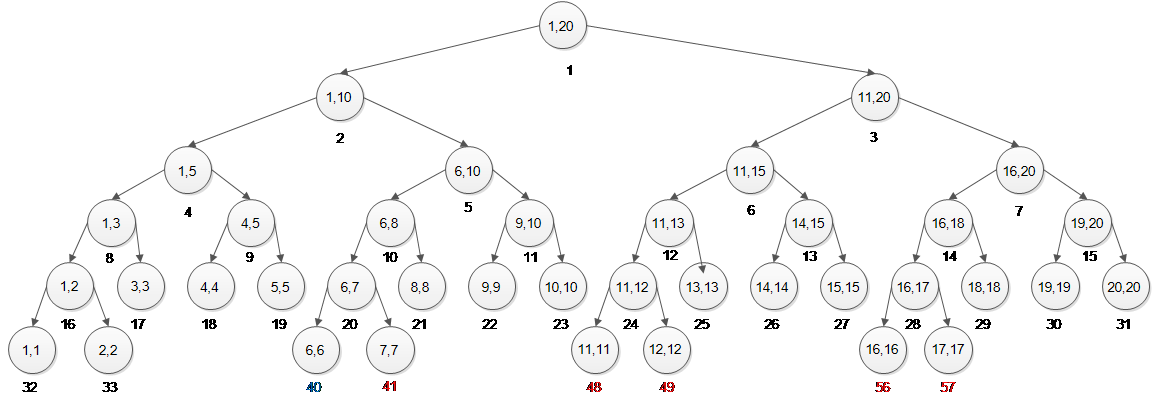
线段树（segment tree）是一种二叉树，与区间树相似，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点，用于维护区间信息。

一棵线段树，记为节点tree[rx]维护区间(l,r)的信息，区间的长度r - l记为L，递归定义为：

若L > 1：设m = l + (r - l ) / 2，则tree[rx]的左儿子是tree[rx * 2]维护区间[l, m]的信息，右儿子是tree[rx * 2 + 1]维护区间[m + 1, r]的信息
若L = 1：则tree[rx]为一个叶子节点，维护[l,r]区间，此时l = r

这里写图片描述

线段树有如下如下函数：

1.建树
2.询问[L, R]区间的和（或极值）
3.将区间[L, R]每个元素的加上val
【注】：将询问某点的情况，当作一个区间看待，修改某个点同理

所以线段树能完成的如下功能：

1.单点询问
2.单点更新
3.区间询问
4.区间更新

下面以查询区间和，修改区间值为例介绍线段树。

求极值的情况类似，这里不在举例。

建树：

void bulid(int rx, int l, int r)，即建立当前节点的标号是rx，维护[l, r]区间的信息的树。

1.如果l = r，则当前节点只需维护一个点的信息
2.否则创建tree[rx]的左子树，创建tree[rx]的右子树
3.合并tree[rx]的左右子树

//建树的节点是rx，tree[rx] 表示l到r的和
void bulid(int rx, int l, int r)
{
    //只需维护一个点的信息
    if(l == r)
    {
        tree[rx] = arr[l];// or arr[r];
        return ;
    }
    //创建左子树
    bulid(rx * 2, l, (l + r) / 2);
    //创建右子树
    bulid(rx * 2 + 1, (l + r)/ 2 + 1, r);
    //合并左右子树的和
    tree[rx] = tree[rx * 2] + tree[rx * 2 + 1];
}

建树，只需要一次即可完成，时间复杂度 $O(nlogn)$ 。

询问区间[L, R]的和：

[L, R]区间的和可以划分为部分小的区间之和。
int query(int rx, int l, int r, int L, int R)，即当前节点是rx，所维护的区间是[l, r]，要查询[L, R]的和

1.若区间[l, r]跟[L, R]完全没有关系，即 $R < l或者 r < L$ ，则表明当前这个区间不是[L, R]的部分和，故此部分贡献的和是0，返回0
2.若[L, R]区间完全包含区间[l, r]，即 $L<= l 并且 r <= R$ ,则这部分和是区间[L, R]和的一部分，返回tree[rx]的值
3.否则这两个区间交叉了，此时[L, R]区间的和就是区间[l, (r - l) / 2]的部分区间加上区间[(r - l) / 2 + 1, r]的部分和，返回这两部分和。

//查询L到R的和
int query(int rx, int l, int r, int L, int R)
{
    //两区间完全不包含
    if(R < l || r < L) return 0;
    //两区间完全包含
    if(L >= l && r <= R) return tree[rx];
    //两区间交叉，返回左子树的和加右子树的和
    return query(rx * 2, l, (l + r) / 2, L, R) + query(rx * 2 + 1, (l + r) / 2 + 1, r, L, R);
}

线段树上每层的节点最多会被选取2个，一共选取的节点数也是 $O(log n)$ ，因此查询的时间复杂度也是 $O(logn)$ 。

更新区间[L, R]

void update(int rx, int l, int r, int L, int R, int val)，即当前节点为rx，维护区间[l, r]的和，将区间[L, R]区间的每个元素加上val

1.如区间[l, r]跟[L, R]完全没有关系，即 $R < l或者 r < L$ ，则表明当前这个区间不需要更新
2.若[L, R]区间完全包含区间[l, r]，即 $L<= l 并且 r <= R$ ，则这部分和是区间[L, R]和的一部分，则应将区间[l, r]的值更新
3.更新左子树，更新右子树
4.合并左右子树的和

//区间更新
void update(int rx, int l, int r, int L, int R, int val)
{
    //区间完全不包含
    if(R < l || r < L) return ;
    //区间完全包含
    if(L <= l && r <= R) 
    {
        tree[rx] += (r - l + 1) * val;
        return ;
    }
    //更新左子树
    update(rx * 2, l, (l + r) / 2, L, R, val);
    //更新右子树
    update(rx * 2 + 1, (l + r) / 2 + 1, r, L, R, val);
    //合并左右子树
    tree[rx] = tree[rx * 2] + tree[rx * 2 + 1];
}

更新区间，几乎想到会更新到[L, R]区间下的所有节点，其实跟建树差不多，时间复杂度 $O(nlogn)$ 。
现在分析一下总的时间复杂度，建树 $O(nlogn)$ ，查询 $O(logn)$ ，更新 $O(nlogn)$ ，共q次询问，总时间复杂度 $O(qnlogn)$ ，呃呃呃，怎么时间复杂度更高了，怎么用了线段树怎么更高了。
其实不然，线段树还得有一种优化叫做Lazy操作,中文翻译叫做懒操作，咋一看名字就不由想到发明这种操作的人肯定是个懒人，但是万事没有绝对的。
这种懒操作是这样的：当更新区间的时候，并不是将该更新的区间的叶子节点都更新，而是将更新一部分。用一个数组add[]记录某个节点所包括的区间需要更新的值，当询问区间的值的时候，并不是将所有的更新信息都更新。举个例子：假设要改变[L, R]区间的值，但是接下来所有的询问中都不会询问到[L, R]的子区间的和，即询问区间没有[L1, R1]， $L<L1 并且R1 < R$ ，所以继续更新下去是没有任何意义的，故若在询问过程中，你需要查询tree[rx]的值，那么就将这个区间的更新的值下放（pushdown），这一点很重要，这也是为什么线段树高效的原因之一吧。

//下放rx更新的值，记录在add[]数组里
void pushdown(int rx, int l, int r)
{
    //如果add[rx]不等于0，则下放更新值
    if(add[rx] != 0)
    {
        //下放到左右子树
        add[rx * 2] += add[rx];
        add[rx * 2 + 1] += add[rx];
        //更新左右子树
        tree[rx * 2] += ((l + r) / 2 - l + 1) * add[rx];
        tree[rx * + 1] += （r - （l + r） / 2 - 1） * add[rx];
        add[rx] = 0;
    }
}

//将更新区间完全包含的情况修改
if(L <= l && r <= R) 
{
    tree[rx] += (r - l + 1) * val;
    add[rx] += val;
    return ;
}

//在询问的时候，下放add[rx]的更新
pushdown(rx, l, r);

有了Lazy操作之后，实践证明可将时间查询的时间复杂度降为 $O(logn)$ 。

完整代码，仅供参考：

/*
    Author: Royecode
    Date: 2015-7-16
*/
#include <iostream>
#define m l + (r - l) / 2
#define lson rx * 2, l, m
#define rson rx * 2 + 1, m + 1, r
#define MAXN 100005
using namespace std;
int tree[MAXN*4], add[MAXN*4];//开4倍的空间

//下放
void pushdown(int rx, int l, int r)
{
    if(add[rx] != 0)
    {
        add[rx * 2] += add[rx];
        add[rx * 2 + 1] += add[rx];
        tree[rx * 2] += (m - l + 1) * add[rx];
        tree[rx * 2 + 1] += (r - m) * add[rx];
        add[rx] = 0;
    }
}

//建树
void bulid(int rx, int l, int r)
{
    if(l == r)
    {
        cin >> tree[rx];
        return ;
    }
    bulid(lson);
    bulid(rson);
    tree[rx] = tree[rx * 2] + tree[rx * 2 + 1];
}

//更新区间
void update(int rx, int l, int r, int L, int R, int v)
{
    if(R < l || L > r) return;
    if(L <= l && r <= R)
    {
        tree[rx] += (r - l + 1) * v;
        add[rx] += v;
        return ;
    }
    update(lson, L, R, v);
    update(rson, L, R, v);
    tree[rx] = tree[rx * 2] + tree[rx * 2 + 1];
}

//询问区间
int query(int rx, int l, int r, int L, int R)
{
    if(R < l || L > r) return 0;
    pushdown(rx, l, r);
    if(L <= l && r <= R) return tree[rx];
    return query(lson, L, R) + query(rson, L, R);
}

int main()
{
    int n, q;
    cin >> n >> q;
    bulid(1, 1, n);
    while(q--)
    {
        int op; //操作类型1.更新区间2.查询区间
        cin >> op;
        if(op == 1)
        {
            int L, R, v;
            cin >> L >> R >> v;
            update(1, 1, n, L, R, v);
        }
        else
        {
            int L, R;
            cin >> L >> R;
            cout << query(1, 1, n, L, R) << endl;
        }
    }
    return 0;
}

需要维护的区间是[1, n]，共n个元素，[1, n]会分为[1, (1 + n) / 2]和[(1 + n) / 2 + 1, n]…..，一直会分下去，直到左边界等于右边界。所以总共有 $2*n-1$ 个节点，此处的线段树是用一个数组模拟一颗树，应将线段树理解成满二叉树，故总共的节点是 $2的(logn+1)幂个$ ，经实践证明小于4*n个，故这个线段树大空间应开 $tree[n*4]$ 。当n=q时，总时间复杂度为 $O(nlogn)$ ，相比朴素的方法，降低了时间复杂度。