今天专题是数论 曾yl大佬给我们讲的 太强了 我要赞美他...!!!
好了进入正题
今天大概有四个内容
1.容斥原理 2.欧拉函数
3.同余 4.莫比乌斯函数
进入主题
容斥
有个口诀 奇加偶减
差不多是这样子 没什么好讲的 上道例题 bzoj1042
这道题可以先用没有限制的背包跑出装满i的容量有多少种方法 用dp[i]表示
但是每种硬币都有限度 怎么办呢
第i种硬币是不是用di + 1 枚就是超出限制了呀 那么容量为si - ci * (di +1)就是容量超出限制不合法方案数
那么就用dp[s] - dp[si - ci * (di +1)]就好了 以此类推 (需要特判不合法容量是否大于0)
然饿这样是错的...
为什么呢 我们很容易发现方案中会出现1号硬币不合法同时2号也不合法的方案
我们在减一号不合法方案和二号时减了两次 多减了一次 怎么办呢 加回来就好了啊...
以此类推 就发现这满足容斥原理 就奇加偶减 就好了
使用递归实现加减不好写的容斥原理
差不多就这。
同余
1.同余的同除性
因为(d,c) = 1 所以d有在模c意义下的逆元(数论倒数)
所以在同余式两边同时乘以d的逆元就好了 而不是两边同时除以d
2.gcd实质
平常我们使用辗转相除法求(a,b) 正确性是因为这个
使用乘法分配律 将gcd提出来 发现y + x 与 y - x 仍然有这个因子
模就相当于一直减一直减就好了
利用这个 就有了一个常数很小的求gcd的板子
先将x y 都变成奇数 将他们的2提出来 取min就相当于把gcd里的2都提出来
然后再辗转相减 因为此时开始x y 是奇数 肯定没有因子2 但是相减出现了偶数 所以位运算弄掉x身上的2。
3.逆元的线性递推
A[i] 表示i的逆元
证明 :
p ≡ 0 (mod p) 将p变成 p / i * i + p % i ≡ 0 令p / i为r ,p % i 为k
有 r * i + k ≡ 0 两边同乘 r k 逆元 (k (-1)) 有 i * k (-1) + r (-1) ≡ 0
移过去 代回去 得证
4.威尔逊定理
证法大概是 1 2 3 4 .... p - 1是p的一个完全剩余系 (概念自个儿查去)
然后有个定理是1 ~ p - 1 内只有1 和 p - 1 他们mod p的逆元是他们自己 别的数都可以两两配对
别问我怎么整的 没讲
然后就配对呗.. 配完了就完了
5.费马小定理 (a p 互质)
证明 :
引理 : 给定一个p的最小的完全剩余系(1 2 3 ... p - 1) 这个剩余系里每个元素乘上一个与p互质的数a后仍然是p的一个完全剩余系
证明引理 : 反证法 假设原本剩余系中两元素 k1 k2 乘上a之后余数相同 (即不满足完全剩余系性质)
则a * k1 - a * k2 ≡ 0 -> a * (k1 - k2) ≡ 0
因为 a p 互质 且p为质数 那么剩余系里的两个元素k1 k2与p互质 所以k1 - k2 也与p互质 所以不可能≡0
假设错误 所以乘上a之后仍然是完全剩余系
所以我们得到了一个新的剩余系 将这两个剩余系自己的所有元素乘起来 显然这两个乘积是同余的
有 1 * 2 * 3 * 4 * .... * (p - 1) ≡ a ^ (p - 1) * 1 * 2 * 3 * 4 * .... * (p - 1) (mod p)
显然1 * 2 * 3 * 4 * .... * (p - 1) 与 p 互质
再有同余的同除性两边乘上1 * 2 * 3 * 4 * .... * (p - 1) 的逆元 即有a ^ (p - 1) ≡ 1 (mod p) 得证
6.BSGS 算法 (c is prime,a c 互质)
用处 求解 a ^ x ≡ b (mod c) 的解x
做法
先令j从1 ~ c 预处理出所有的a ^ j mod c 用数字哈希存入一个邻接表中
将这个转化为根号下算法 令m = √c 就有x = i * m + j ( 0 <= i <= √c)
那么我们就枚举 i
令D = a ^ (i * m) 有 D * a^j ≡ b (c) 令X = a^j -> DX + c * y ≡ b (c)
这是不是一个同余方程呀! 用exgcd求解即可 求得的X0再用 X0 + k * c / (a,c) 包括所有可行解
在这样求得最小正整数解 再去hash表中找是否有对应的a ^ j 如果有 就求出来了...
exgcd貌似讲的时候出了点小问题 以后有时间来弄吧..
同余差不多
欧拉函数 概念自个儿查去
先给你三个定理 (zyl大哥手写第三条..)
要求p is prime.
证明定理1 :
还是比较容易的 因为p是一个质数 那么每隔p个数出现一个p的倍数 只有这个倍数才与p不互质
所以p ^ k 个数里 有 p ^ k / p 个数不与p互质 也就是p ^ (k - 1)
作差得证
证明定理2 :
首先将n进行质因数分解 n = p1 ^ r1 * p2 ^ r2 ... pk ^ rk (pi是n的因数)
然后我们需要知道phi函数是一个积性函数 概念自个儿查去
再分别对pi ^ ri 使用定理1 有phi(n) = phi(p1 ^ r1) * phi(p2 ^ r2 )...* phi(pk ^ rk ) =
p1 ^ r1 * p2 ^ r2 ... pk ^ rk * (1 - 1/p1) * (1 - 1/p2)* ....(1 - 1/pk) 把前面那一大坨代成n 得证
证明定理3 :
我们对1 ~ n的所有数进行分组
我们令cd 为(i,n) = d 的一个集合 |cd|表示这个集合的元素个数
那么我们能保证1 ~ n 里的每一个数都能分且只能分进一组当中
因为(i,n)只有一个且必有(1,n)
满足条件的(i,n) = d 同时除以d -> (1 / d,n / d) = 1 这是什么? 是phi(n / d) 啊
也就是说|cd| = phi(n / d)
并且我们发现每一个i只能分入cd (d | n)的组里 因为d必定是n的因子
所以统计时只需要统计能整除n的d 的|cd|就好了
换句话说 ∑|cd| (d | n) = ∑phi(n / d) (d | n) = (将n / d转化成n的因子d是等价的) = ∑phi(d) (d | n) =
集合中所有元素的个数 = n
得证
用定理2可以求单个数的phi值
欧拉线性筛
不多说了只需要知道两个定理
phi(n * m) = phi(m) * phi(n) (m n 互质 n is prime)
phi(n * m) = phi(m) * n (m n 不互质 n is prime 也就是m是n的倍数)
欧拉定理
证明
首先我们需要知道什么是缩系(既约剩余系) 概念自个儿查去
现在我有一个1 ~ n 的完全缩系(p1 p2 p3 p4 ... pk) 将这个缩系中 每个元素乘上a (a n 互质)
我们很容易知道若一个数其余数原本与n互质 则它乘上一个与n 互质的数a之后 模n余数仍然与n互质
又因为他原是一个完全剩余系 那么现在肯定还是一个完全剩余系
(因为元素mod n余数两两不同 证明方法与上述费马小定理中引理的证明相同)
所以将这个缩系里每个元素相乘 由缩系概念可知 缩系元素的个数肯定是phi(n) 即k = phi(n)
有p1 * p2 * p3 * ... pk ≡ p1 * p2 * p3 * ... pk * a ^ k
又由同余的同除性有 a ^ phi(n) ≡ 1 (mod n)
扩展欧拉定理
别问了我也不会证明 没讲
先写这么多吧 莫比乌斯函数写不完了...









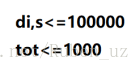




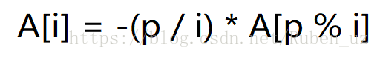

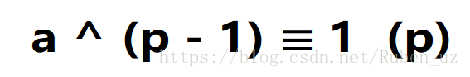
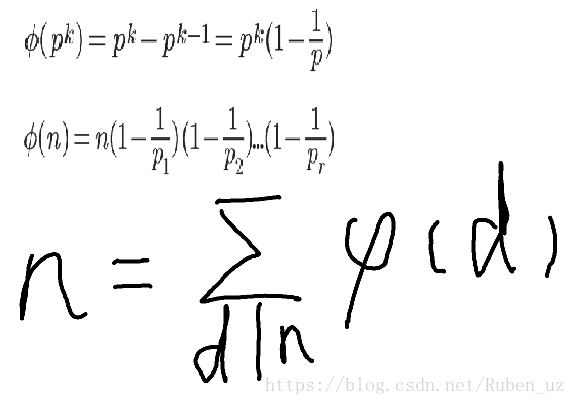



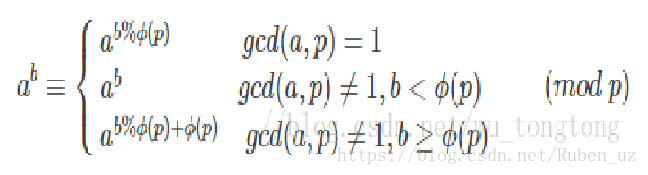













 695
695











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








