【复杂网络学习笔记】2：无标度网络的建立_选取一个无标度网络利用主方程法求模型的入度分布-CSDN博客

本文链接：https://blog.csdn.net/SHU15121856/article/details/71308176

scale - free network, 现实世界的网络大部分都不是随机网络，少数的节点往往拥有大量的连接，而大部分节点却很少，一般而言他们符合二八定律。将度分布符合幂律分布的复杂网络称为无标度网络。

如互联网，大型软件的结构特性都属于无标度网络：

只要攻击那些度数很多的关键节点就能引起最大的攻击效益。

这也正体现了无标度网络对蓄意攻击的脆弱性(李青老师用了一个有趣的阿喀琉斯踵的故事)，总结如下：

*通用异常类Error.h

#ifndef ERROR_H
#define ERROR_H
#include<iostream>
using namespace std;
//通用异常类
class Error
{
private:
	char message[100];//异常信息
public:
	Error(const char *mes = "一般性异常!"); //构造函数 
	~Error(void) {}; //析构函数	
	void Show() const; //显示异常信息
};

Error::Error(const char *mes)
{
	strcpy_s(message, 100, mes); //复制异常信息
}

void Error::Show()const
{
	cout << message << endl; //显示异常信息	
}
#endif

*无向图邻接网的边节点类Arc.h

#ifndef NULL
#define NULL (void *)0
#endif

#ifndef ARC_H
#define ARC_H

//边节点类
struct Arc
{
	int iNum; //弧的另一端的节点的序号
	Arc* pNext; //指向下一边节点的指针

	Arc(int n, Arc* next); //构造序号为n，下一节点指向next的边节点
};
Arc::Arc(int n, Arc* next)
{
	iNum = n;
	pNext = next;
}
#endif

*无向图邻接表的顶点节点类Vex.h

#ifndef NULL
#define NULL 0
#endif

#ifndef VEX_H
#define VEX_H
#include "arc.h"
struct Vex
{
	int k;//度数
	Arc* pFirst; //指向边节点表
	Vex();//空构造
};
Vex::Vex()
{
	k = 0;//度数一开始为0
	pFirst = NULL;
}
#endif

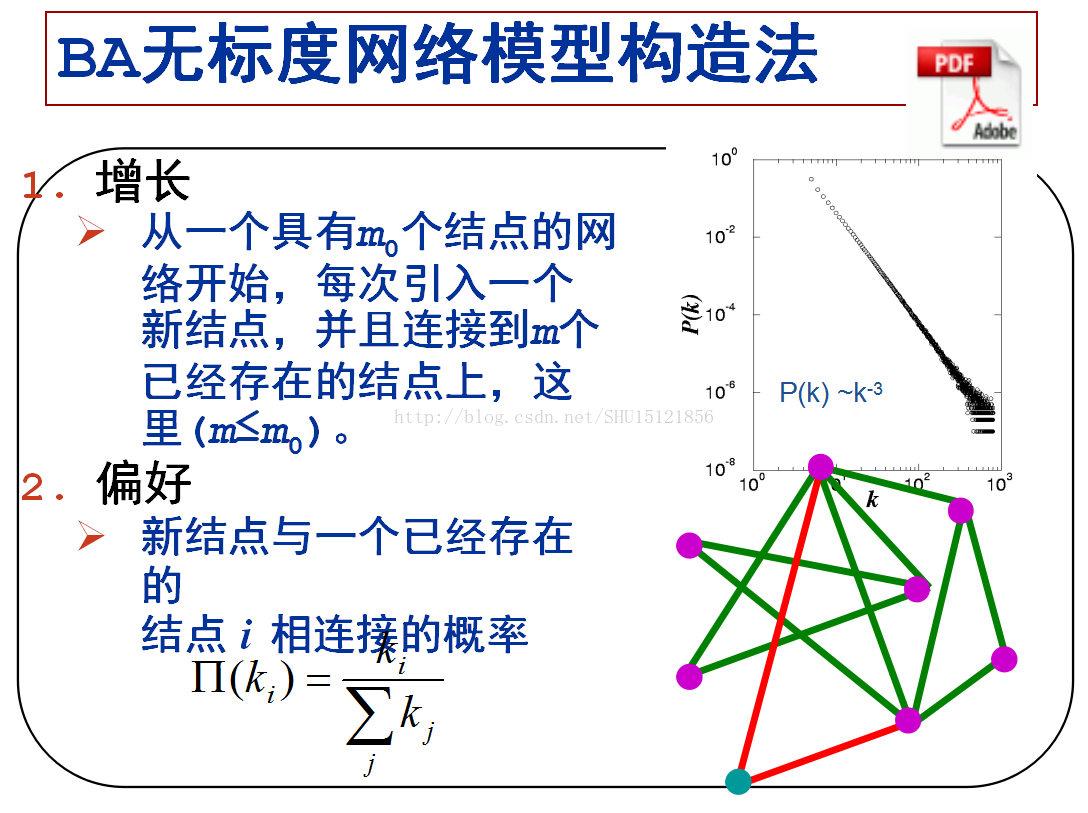
这里补充一下无标度网络的生成过程，直接搬老师PPT好了：

*邻接网络(无标度模型)类NetWork.h

#ifndef NULL
#define NULL (void *)0
#endif

#ifndef NETWORK_H
#define NETWORK_H
#include "vex.h"
#include "error.h"
#define N 4//最近邻网络

//邻接网络(无标度模型)类
struct NetWork
{
	int vexNum; //顶点的数目
	Vex* vexTable; //顶点表
	int maxNum;//最大数目
	int numMod;//k值总和，用于求余

	NetWork(int v,int n); //构造有v个顶点的空表
	void Clear(); //清空边节点
	void BuildArc(int a, int b); //构造从a到b的边
	void Step1(); //清空全表，然后形成部分最近邻网络
	void Step2();//每次引入一个新节点，以概率连接到之前的点上
	void Show(); //简易的显示该网络
	void DelArc(int a, int b); //删除从a到b的边
	bool HasArc(int a, int b); //查询是否有从a到b的边
};

NetWork::NetWork(int v,int n) //构造有v个顶点，最大为n的空表
{
	if (n < v)
		throw Error("n不能比v小");
	vexTable = new Vex[maxNum = n];
	vexNum = v;
	numMod = 0;
}

void NetWork::Clear() //清空边节点
{
	Arc* p;
	for (int i = 0; i < vexNum; i++)
	{
		p = vexTable[i].pFirst; //从第一个边节点开始
		while (p != NULL)
		{
			vexTable[i].pFirst = p->pNext; //first域连到p后去
			delete p; //删掉p
			p = vexTable[i].pFirst; //再次指向first的节点
		}
		vexTable[i].k = 0;
	}
	numMod = 0;//清空numMod
}

void NetWork::DelArc(int a, int b) //删除从a到b的边
{
	if (a < 0 || b < 0 || a >= vexNum || b >= vexNum)
		throw Error("数组越界");
	if (a == b)
		throw Error("自身没有环");
	Arc *p, *q;
	//删除a->b
	if (vexTable[a].pFirst->iNum == b) //如果是第一个点
	{
		p = vexTable[a].pFirst;
		vexTable[a].pFirst = p->pNext;
		delete p;
		vexTable[a].k--;
		numMod -= 2;//维护
	}
	else //如果不是第一个点
	{
		q = vexTable[a].pFirst; //q在p前
		p = q->pNext;
		while (p != NULL)
		{
			if (p->iNum == b) //找到了b的位置
			{
				q->pNext = p->pNext;
				delete p;
				vexTable[a].k--;
				numMod -= 2;//维护
				break;
			}
		}
	}
	//删除b->a
	if (vexTable[b].pFirst->iNum == a) //如果是第一个点
	{
		p = vexTable[b].pFirst;
		vexTable[b].pFirst = p->pNext;
		delete p;
		vexTable[b].k--;
		numMod -= 2;//维护
	}
	else //如果不是第一个点
	{
		q = vexTable[b].pFirst; //q在p前
		p = q->pNext;
		while (p != NULL)
		{
			if (p->iNum == a) //找到了a的位置
			{
				q->pNext = p->pNext;
				delete p;
				vexTable[b].k--;
				numMod -= 2;//维护
				break;
			}
		}
	}
}

bool NetWork::HasArc(int a, int b) //查询是否有从a到b的边
{
	if (a < 0 || b < 0 || a >= vexNum || b >= vexNum)
		throw Error("数组越界");
	if (a == b)
		throw Error("自身没有环");
	Arc* p;
	bool k = 0; //k=1时表示从a到b有边
	p = vexTable[a].pFirst; //不妨看a->b有没有，从第一个边节点开始
	while (p != NULL) //检索是否已经有边
	{
		if (p->iNum == b) //检索到，做标记并跳出
		{
			k = 1;
			break;
		}
		p = p->pNext; //没检索到，继续找
	}
	return k;
}

void NetWork::BuildArc(int a, int b) //建立从a到b的边
{
	if (a < 0 || b < 0 || a >= maxNum || b >= maxNum)
		throw Error("数组越界");
	if (a == b)
		throw Error("不能自身成环");
	Arc* p;
	bool k = 0; //k=1时表示从a到b有边
	p = vexTable[a].pFirst; //不妨看a->b有没有，从第一个边节点开始
	while (p != NULL) //检索是否已经有边
	{
		if (p->iNum == b) //检索到，做标记并跳出
		{
			k = 1;
			break;
		}
		p = p->pNext; //没检索到，继续找
	}
	if (k == 0) //如果没有边，建立之
	{
		vexTable[a].pFirst = new Arc(b, vexTable[a].pFirst); //a能找到b同时
		vexTable[b].pFirst = new Arc(a, vexTable[b].pFirst); //b也要能找到a
		vexTable[a].k++;
		vexTable[b].k++;
		numMod += 2;//维护
	}
}

void NetWork::Step1() //清空全表，然后形成部分近邻网络
{
	int n;
	if (N > vexNum)
		n = 2;
	else
		n = N;
	Clear(); //清空
	for (int i = 0; i < vexNum; i++) //对每个节点i
	{
		for (int j = 1; j <= n / 2; j++) //建立其n最近邻关系
		{
			BuildArc(i, (i + j) % vexNum); //向后第j个
			BuildArc(i, (i - j + vexNum) % vexNum); //向前第j个
		}
		vexTable[i].k = n;//度数肯定为n，这句可有可无，Build时已经做好了
	}
	numMod = n*vexNum;//初始化，这句可有可无，Build时已经做好了
}

void NetWork::Step2()
{
	int randomNum;//存储随机数
	int sum = 0;//sum用于寻找这个随机数落在哪里，这样就形成了概率
	for (int i = vexNum; i < maxNum; i++)//对后面未建立的每个节点
	{
		sum = 0;//每次sum都清空
		randomNum = rand() % numMod;//只要对numMod取余就一定在0~numMod之间
		for (int j = 0; j < i; j++)
		{
			sum += vexTable[j].k;//sum不断加上这个k值
			if (sum>randomNum)//说明落在这里
			{
				BuildArc(i, j);//函数里面已经对k值和numMod进行维护了
				break;//找到后跳出小for()
			}
		}
	}
	vexNum = maxNum;//执行完后vexNum可以充满整个数组
}

void NetWork::Show() //显示
{
	Arc* p; //辅助指针
	cout << "一共可以存" << maxNum << "个节点" << endl;
	for (int i = 0; i < vexNum; i++)
	{
		cout << i << "("<<vexTable[i].k<<"):";
		p = vexTable[i].pFirst; //从第一条边开始
		while (p != NULL) //对于每条边
		{
			cout << "->" << p->iNum;
			p = p->pNext;
		}
		cout << endl;
	}
}
#endif

*程序入口wbd.cpp

// wbd.cpp : 定义控制台应用程序的入口点。
//

#include "stdafx.h"
#include <iostream>
#include "NetWork.h" //邻接网络(无标度模型)类
using namespace std;
#define OK 25
#define MAXI 100
int _tmain(int argc, _TCHAR* argv[])
{
	try{
		cout << "建立空网络(" << OK << "," << MAXI << ")后：" << endl;
		NetWork *pNet = new NetWork(OK,MAXI); //建立空网络(有效OK，满MAXI)
		pNet->Show(); //显示看一下

		cout<<endl << "形成N最近邻网络后：" << endl;
		pNet->Step1(); //对有效点形成N最近邻网络
		pNet->Show(); //显示看一下

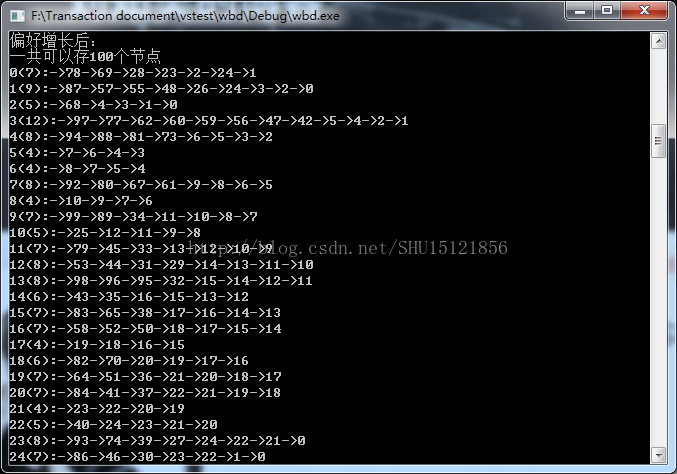
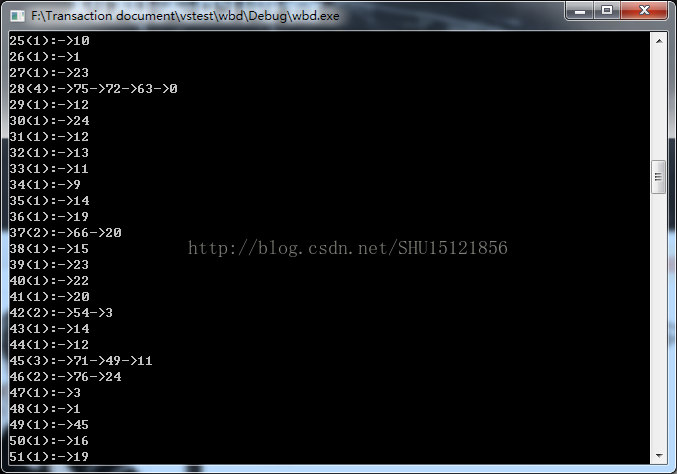
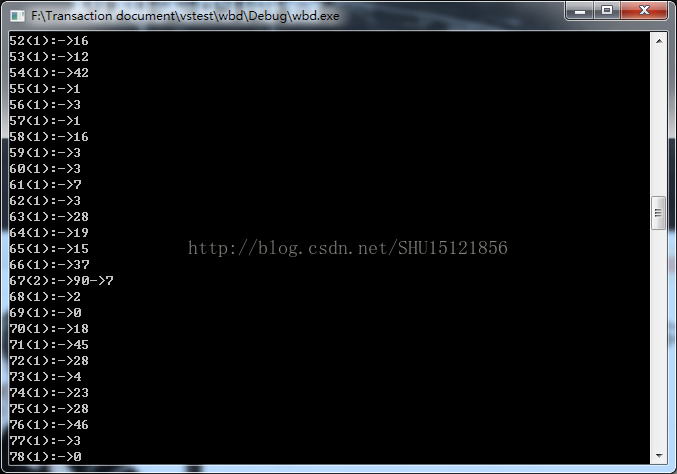
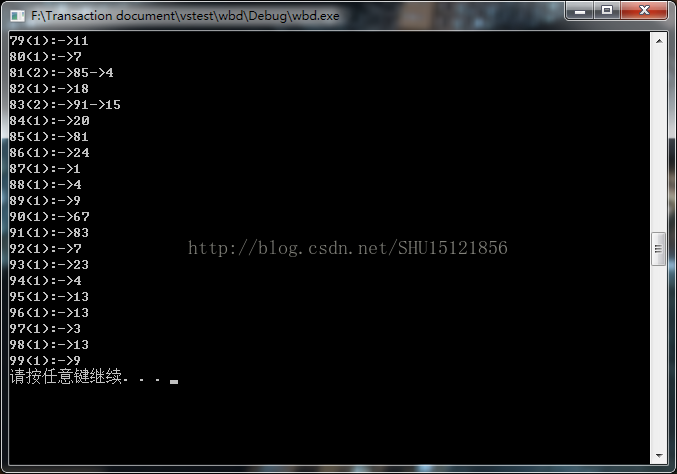
		cout <<endl<< "偏好增长后：" << endl;
		pNet->Step2(); //偏好增长
		pNet->Show(); //显示看一下
		system("pause");
		return 0;
	}
	catch (Error er)
	{
		er.Show();
	}
	return 0;
}

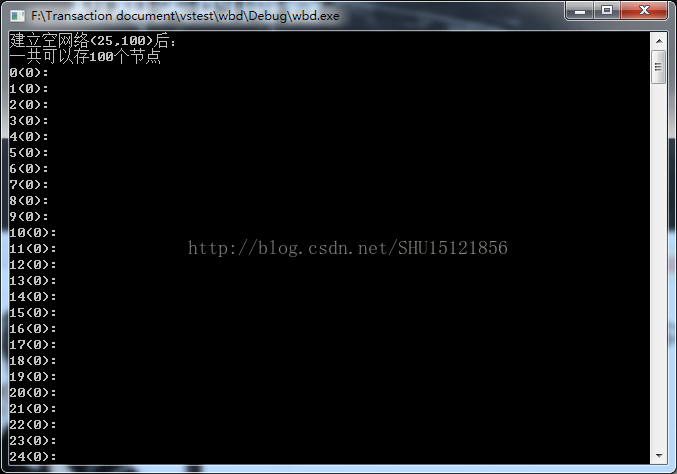
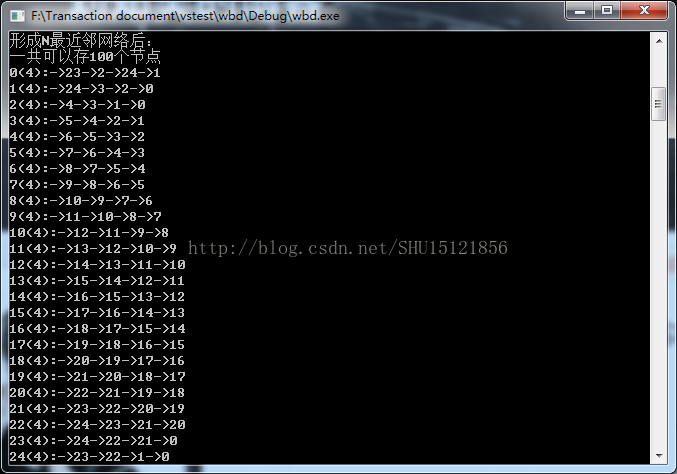
运行结果：

先生成空网络，我这里有效=25，开的数组=100