深入理解时间复杂度:从理论到C++实践
文章目录
什么是时间复杂度?
在计算机科学中,时间复杂度是描述算法执行时间随输入数据规模增长而变化趋势的度量。它不关注具体的执行时间(比如多少毫秒),因为这些会受到编程语言、CPU速度、内存等硬件因素的影响。相反,它关注的是一个宏观的、趋势性的关系。
想象一下,你要处理1000条数据和100万条数据,时间复杂度告诉我们算法性能会如何变化——是几乎不变,线性增长,还是爆炸式增长?
大 O 表示法:时间复杂度的标准语言
我们使用大 O 表示法来描述时间复杂度,它表示算法执行时间的上界,即最坏情况下的复杂度。
大 O 表示法的核心规则:
- 忽略常数项:
O(2n)和O(100n)都记作O(n) - 只保留最高次项:
O(n² + n + 1000)记作O(n²) - 忽略系数:
O(3n²)记作O(n²)
常见时间复杂度详解及C++示例
1. O(1) - 常数时间复杂度
描述:执行时间不随输入规模 n 变化,无论数据量多大,执行时间固定。
C++示例:
#include <iostream>
#include <vector>
using namespace std;
// O(1) - 访问数组元素
int getFirstElement(const vector<int>& arr) {
return arr[0]; // 无论数组多长,直接返回第一个元素
}
// O(1) - 哈希表查找(平均情况)
#include <unordered_map>
int hashLookup(const unordered_map<int, string>& map, int key) {
auto it = map.find(key);
return it != map.end() ? 1 : 0;
}
2. O(log n) - 对数时间复杂度
描述:执行时间随 n 增长呈对数增长,效率极高。
C++示例 - 二分查找:
#include <vector>
using namespace std;
int binarySearch(const vector<int>& arr, int target) {
int low = 0;
int high = arr.size() - 1;
while (low <= high) {
int mid = low + (high - low) / 2; // 防止溢出
if (arr[mid] == target) {
return mid;
} else if (arr[mid] < target) {
low = mid + 1;
} else {
high = mid - 1;
}
}
return -1; // 未找到
}
// 每一步搜索范围减半,复杂度 O(log n)
3. O(n) - 线性时间复杂度
描述:执行时间与 n 成正比。
C++示例:
#include <vector>
#include <climits>
using namespace std;
// O(n) - 查找最大值
int findMax(const vector<int>& arr) {
if (arr.empty()) return INT_MIN;
int maxVal = arr[0];
for (size_t i = 1; i < arr.size(); ++i) { // 循环 n 次
if (arr[i] > maxVal) {
maxVal = arr[i];
}
}
return maxVal;
}
// O(n) - 数组求和
int arraySum(const vector<int>& arr) {
int sum = 0;
for (int num : arr) { // 遍历所有元素
sum += num;
}
return sum;
}
4. O(n log n) - 线性对数时间复杂度
描述:许多高效排序算法的复杂度。
C++示例 - 归并排序:
#include <vector>
using namespace std;
void merge(vector<int>& arr, int left, int mid, int right) {
vector<int> temp(right - left + 1);
int i = left, j = mid + 1, k = 0;
while (i <= mid && j <= right) {
if (arr[i] <= arr[j]) {
temp[k++] = arr[i++];
} else {
temp[k++] = arr[j++];
}
}
while (i <= mid) temp[k++] = arr[i++];
while (j <= right) temp[k++] = arr[j++];
for (int p = 0; p < k; ++p) {
arr[left + p] = temp[p];
}
}
void mergeSort(vector<int>& arr, int left, int right) {
if (left >= right) return;
int mid = left + (right - left) / 2;
mergeSort(arr, left, mid); // 递归左半部分
mergeSort(arr, mid + 1, right); // 递归右半部分
merge(arr, left, mid, right); // 合并 O(n)
}
// 递归深度 O(log n),每层合并操作 O(n),总复杂度 O(n log n)
5. O(n²) - 平方时间复杂度
描述:执行时间与 n² 成正比,数据量大时性能急剧下降。
C++示例:
#include <vector>
using namespace std;
// O(n²) - 冒泡排序
void bubbleSort(vector<int>& arr) {
int n = arr.size();
for (int i = 0; i < n - 1; ++i) { // 外层循环 n 次
for (int j = 0; j < n - i - 1; ++j) { // 内层循环 ~n 次
if (arr[j] > arr[j + 1]) {
swap(arr[j], arr[j + 1]);
}
}
}
// 总操作次数 ~ n * n,复杂度 O(n²)
}
// O(n²) - 打印所有数对
void printAllPairs(const vector<int>& arr) {
int n = arr.size();
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
cout << "(" << arr[i] << ", " << arr[j] << ") ";
}
cout << endl;
}
}
6. O(2^n) - 指数时间复杂度
描述:执行时间呈指数级增长,只能处理小规模问题。
C++示例 - 斐波那契数列(低效版本):
// O(2^n) - 斐波那契数列(递归)
int fibonacci(int n) {
if (n <= 1) return n;
return fibonacci(n - 1) + fibonacci(n - 2);
// 递归树呈指数级增长
}
// 优化版本 - 动态规划 O(n)
int fibonacciDP(int n) {
if (n <= 1) return n;
vector<int> dp(n + 1);
dp[0] = 0;
dp[1] = 1;
for (int i = 2; i <= n; ++i) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
7. O(n!) - 阶乘时间复杂度
描述:最恐怖的复杂度,通常出现在排列组合问题中。
C++示例 - 生成全排列:
#include <vector>
#include <algorithm>
using namespace std;
void generatePermutations(vector<int>& arr, int start, vector<vector<int>>& result) {
if (start == arr.size()) {
result.push_back(arr);
return;
}
for (int i = start; i < arr.size(); ++i) {
swap(arr[start], arr[i]);
generatePermutations(arr, start + 1, result);
swap(arr[start], arr[i]); // 回溯
}
}
// 排列数为 n!,复杂度 O(n!)
时间复杂度对比分析
不同规模下的表现差异
让我们通过具体数字来感受各种复杂度的差异:
| 复杂度 | n=10 | n=100 | n=1000 | n=10000 |
|---|---|---|---|---|
| O(1) | 1 | 1 | 1 | 1 |
| O(log n) | ~3 | ~7 | ~10 | ~13 |
| O(n) | 10 | 100 | 1000 | 10000 |
| O(n log n) | ~30 | ~700 | ~10000 | ~130000 |
| O(n²) | 100 | 10000 | 10⁶ | 10⁸ |
| O(2ⁿ) | 1024 | 1.3×10³⁰ | 巨大 | 天文数字 |
| O(n!) | 3628800 | 9.3×10¹⁵⁷ | 无法计算 | 无法计算 |
小数据量时的特殊考虑
当数据规模较小时(n < 50),情况会有所不同:
- 常数项的影响:一个
O(n log n)的算法可能因为实现复杂、常数项大,反而不如简单的O(n²)算法 - 缓存友好性:简单算法可能更好地利用CPU缓存
- 实现复杂度:简单算法更易编写和维护
这就是为什么很多标准库的排序函数(如C++的std::sort)在小数组时会切换到插入排序等 O(n²) 算法。
大数据量时的决定性因素
当数据规模很大时(n > 1000),复杂度的等级决定了算法的生死:
O(1),O(log n),O(n):依然高效O(n log n):可接受的性能边界O(n²):需要慎重考虑,可能无法处理大规模数据O(2ⁿ),O(n!):基本不可用
经典时间复杂度趋势图
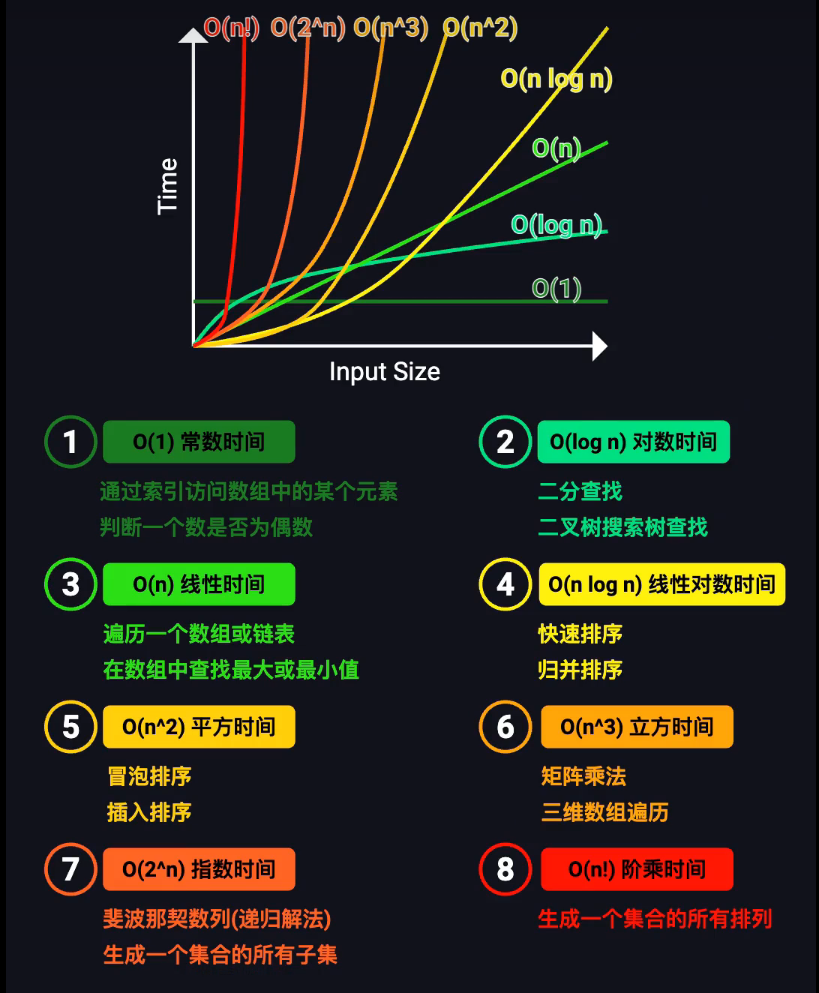
趋势分析:
- O(1):完美水平线,算法的理想状态
- O(log n):几乎贴着X轴的缓慢爬升,效率极高
- O(n):稳定的线性增长,可预测的性能
- O(n log n):高效算法的分界线,很多优秀算法在此
- O(n²):性能悬崖的开始,需要谨慎使用
- O(2ⁿ) 和 O(n!):计算灾难区,只能处理极小规模问题
实际编程中的复杂度分析技巧
1. 循环分析法则
// 单层循环 -> O(n)
for (int i = 0; i < n; ++i) {
// O(1) 操作
}
// 嵌套循环 -> O(n²)
for (int i = 0; i < n; ++i) { // O(n)
for (int j = 0; j < n; ++j) { // O(n)
// O(1) 操作
}
}
// 不同变量的循环 -> O(n × m)
for (int i = 0; i < n; ++i) { // O(n)
for (int j = 0; j < m; ++j) { // O(m)
// O(1) 操作
}
}
2. 递归分析法则
// 二分递归 -> O(log n)
int binarySearch(...) {
// 每次递归问题规模减半
}
// 线性递归 -> O(n)
void linearRecursion(int n) {
if (n <= 0) return;
linearRecursion(n - 1); // 每次递归问题规模减1
}
// 分支递归 -> O(2^n)
int fibonacci(int n) {
if (n <= 1) return n;
return fibonacci(n-1) + fibonacci(n-2); // 两个递归分支
}
3. 常用数据结构的操作复杂度
| 数据结构 | 访问 | 查找 | 插入 | 删除 |
|---|---|---|---|---|
| 数组 | O(1) | O(n) | O(n) | O(n) |
| 链表 | O(n) | O(n) | O(1) | O(1) |
| 哈希表 | O(1) | O(1) | O(1) | O(1) |
| 平衡二叉搜索树 | O(log n) | O(log n) | O(log n) | O(log n) |
总结与实践建议
核心要点回顾
- 时间复杂度是趋势分析工具,帮助我们理解算法随数据规模增长的表现
- 大 O 表示法关注最坏情况,忽略常数和低阶项
- 复杂度等级决定算法 scalability(可扩展性)
工程实践建议
- 优先选择低复杂度算法,但要考虑实际数据规模
- 小数据量时不要忽视简单算法的优势
- 分析代码瓶颈时,重点关注循环和递归
- 利用标准库(如C++ STL),它们已经过充分优化
- 在设计和评审阶段就考虑时间复杂度问题
最后的思考
理解时间复杂度不仅仅是应付面试,更是编写高效、可扩展软件的基础。当你面对大规模数据处理、高性能计算等场景时,这种思维方式将成为你最重要的工具之一。
记住:好的程序员解决问题,伟大的程序员用正确的方式解决问题。时间复杂度分析就是帮助我们找到"正确方式"的重要工具。





















 1224
1224

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








