bzoj4817 [Sdoi2017]树点涂色

传送门

LCT+树链剖分好题。
我们可以记录每一个点到根节点的路径中颜色总数，那么第一问可以用LCT的access解决，第二问可以在树链剖分后用x和y的值减去其LCA的值+1得到；第三问利用树链剖分后对子树的区间查询解决。（感觉说了一通废话）
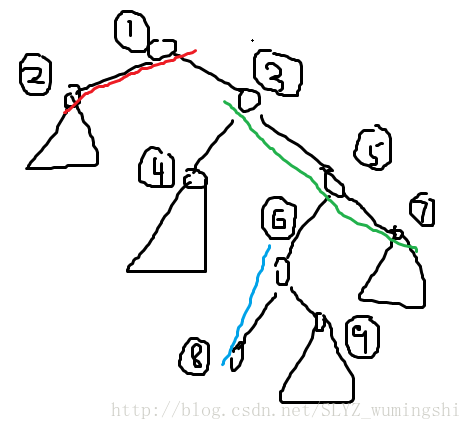
我们可以发现，对任意点来说，其到根节点的路径中颜色总数都是在LCT中路径上轻边的个数加1。那么如果我们对这个点进行第一种操作，显然会对这条链上所有的子树造成影响（画个图比较好讲）：

假设图中的每个点都被标上了颜色，如果我们对6号点进行第一种操作，那么8号点、7号点、2号点及其字数内的值都要加1；而当我们顺次连接5号点和6号点、1号点和3号点时，6号点和3号点的子树内的值要减1。所以我们在access的时候对线段树内的值也进行维护就好了，其余的细节就不说了，具体看代码。

CODE：

#include<cstdio>
#include<algorithm>
using namespace std;
const int N=1e5+10;
struct node
{
    int id;
    node *ch[2],*fa;
    inline int getwh()
    {
        return fa->ch[0]==this?0:1;
    }
    inline bool isroot();
    inline void setch(int wh,node *child);
}pool[N],*null;
inline bool node::isroot()
{
    return fa==null||(fa->ch[0]!=this&&fa->ch[1]!=this);
}
inline void node::setch(int wh,node *child)
{
    ch[wh]=child;
    if(child!=null) child->fa=this;
}
struct edge
{
    int nxt,to;
}a[N<<1];
struct tree
{
    int num,plus;
}t[N<<2];
int head[N],size[N],deep[N],f[N],son[N],pos[N],top[N],s[N];
int n,m,opt,x,y,num,tot;
inline int max(const int &a,const int &b){return a>b?a:b;}
inline int min(const int &a,const int &b){return a<b?a:b;}
inline void swap(int &a,int &b){a^=b,b^=a,a^=b;}
inline void read(int &n)
{
    n=0;char c=getchar();
    while(c<'0'||c>'9') c=getchar();
    while(c>='0'&&c<='9') n=(n<<3)+(n<<1)+c-48,c=getchar();
}
inline void add(int x,int y)
{
    a[++num].nxt=head[x],a[num].to=y,head[x]=num;
    a[++num].nxt=head[y],a[num].to=x,head[y]=num;
}
void dfs(int now,int fa,int depth)
{
    f[now]=fa,deep[now]=depth,size[now]=1;
    pos[now]=++tot,s[tot]=depth;
    if(fa)
    {
        node *Now=pool+now,*Fa=pool+fa;
        Now->fa=Fa;
    }
    int tmp=0;
    for(int i=head[now];i;i=a[i].nxt)
      if(a[i].to!=fa)
      {
        dfs(a[i].to,now,depth+1);
        size[now]+=size[a[i].to];
        if(size[a[i].to]>tmp) tmp=size[a[i].to],son[now]=a[i].to;
      }
}
void dfs2(int now,int high)
{
    top[now]=high;
    if(son[now]) dfs2(son[now],high);
    for(int i=head[now];i;i=a[i].nxt)
      if(a[i].to!=f[now]&&a[i].to!=son[now]) dfs2(a[i].to,a[i].to);
}
inline int LCA(int x,int y)
{
    while(top[x]!=top[y])
      if(deep[top[x]]>deep[top[y]]) x=f[top[x]];
      else y=f[top[y]];
    return deep[x]<deep[y]?x:y;
}
inline void pushdown(int now)
{
    if(!t[now].plus) return;
    int s1=now<<1,s2=now<<1|1;
    t[s1].num+=t[now].plus,t[s1].plus+=t[now].plus;
    t[s2].num+=t[now].plus,t[s2].plus+=t[now].plus;
    t[now].plus=0;
}
inline void update(int now)
{
    t[now].num=max(t[now<<1].num,t[now<<1|1].num);
}
void build(int l,int r,int now)
{
    if(l==r)
    {
        t[now].num=s[l];
        return;
    }
    int mid=(l+r)>>1;
    build(l,mid,now<<1);
    build(mid+1,r,now<<1|1);
    update(now);
}
void Add(int L,int R,int l,int r,int now,int num)
{
    if(L<=l&&r<=R)
    {
        t[now].num+=num,t[now].plus+=num;
        return;
    }
    int mid=(l+r)>>1;
    pushdown(now);
    if(L<=mid) Add(L,R,l,mid,now<<1,num);
    if(R>mid) Add(L,R,mid+1,r,now<<1|1,num);
    update(now);
}
int ask(int L,int R,int l,int r,int now)
{
    if(L<=l&&r<=R) return t[now].num;
    int mid=(l+r)>>1,ans=0;
    pushdown(now);
    if(L<=mid) ans=ask(L,R,l,mid,now<<1);
    if(R>mid) ans=max(ans,ask(L,R,mid+1,r,now<<1|1));
    return ans;
}
inline int Ask(int x,int y)
{
    int lca=LCA(x,y);
    return ask(pos[x],pos[x],1,n,1)+ask(pos[y],pos[y],1,n,1)-(ask(pos[lca],pos[lca],1,n,1)<<1)+1;
}
inline void clear(node *now,int id){now->ch[0]=now->ch[1]=now->fa=null,now->id=id;}
inline void rotate(node *now)
{
    node *fa=now->fa,*grand=fa->fa;
    int wh=now->getwh();
    fa->setch(wh,now->ch[wh^1]);
    if(fa->isroot()) now->fa=grand;
    else grand->setch(fa->getwh(),now);
    now->setch(wh^1,fa);
}
inline void splay(node *now)
{
    for(;!now->isroot();rotate(now))
      if(!now->fa->isroot()) now->getwh()==now->fa->getwh()?rotate(now->fa):rotate(now);
}
inline node *findroot(node *now)
{
    splay(now);
    while(now->ch[0]!=null) now=now->ch[0];
    return now;
}
inline void access(node *now)
{
    node *tmp=null;
    for(;now!=null;tmp=now,now=now->fa)
    {
        splay(now);
        node *root=findroot(tmp);
        if(root!=null) Add(pos[root->id],pos[root->id]+size[root->id]-1,1,n,1,-1);
        root=now->ch[1];now->setch(1,tmp);
        root=findroot(root);
        if(root!=null) Add(pos[root->id],pos[root->id]+size[root->id]-1,1,n,1,1);
    }
}
int main()
{
    null=pool;
    read(n),read(m);
    for(int i=0;i<=n;i++)
      clear(pool+i,i);
    for(int i=1;i<n;i++)
      read(x),read(y),add(x,y);
    dfs(1,0,1),dfs2(1,1),build(1,n,1);
    while(m--)
    {
        read(opt),read(x);
        if(opt==1) access(pool+x);
        else if(opt==2) read(y),printf("%d\n",Ask(x,y));
        else printf("%d\n",ask(pos[x],pos[x]+size[x]-1,1,n,1));
    }
    return 0;
}

总结：
学会一种知识理解其本质才能灵活运用；
一定要注意细节，不然会出现一些奇怪的错误。