镜像二叉树和求二叉树最大深度（java）

镜像二叉树。有些题目叫翻转二叉树。是同一个题。

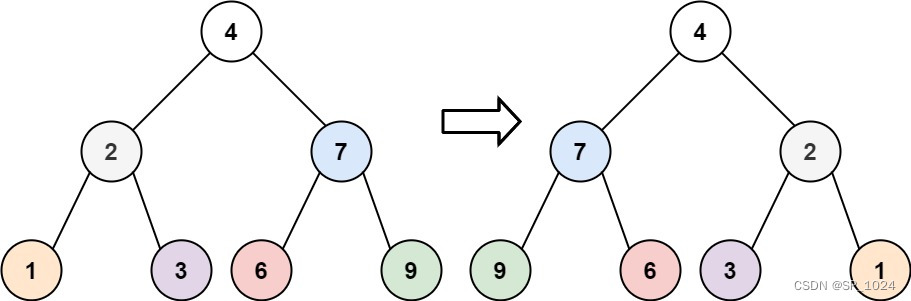
题目描述：给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。
示例：

思路：
这题用递归就很简单，递归左树和右树时，将左右交换下，直接代码演示

* Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode invertTree(TreeNode root) {
        if(root == null){
            return null;
        }
        process(root);
        return root;
    }

    public TreeNode  process(TreeNode root){
        if(root == null){
            return null;
        }
       
        TreeNode left  = process(root.left);
        TreeNode right = process(root.right);
        root.left = right;
        root.right = left;
        return root;
    }
}

LeetCode 原题链接，可以复制代码进去测试

二叉树的最大深度

题目描述：
给定一个二叉树，找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例：

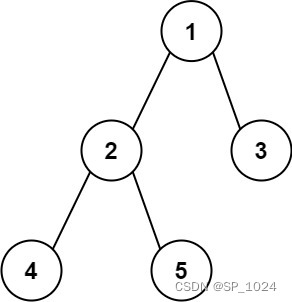
返回它的最大深度 3 。

思路：
使用递归去获取左树和右树的高度，取最大的加顶点1，就是最大高度。
代码如下：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int maxDepth(TreeNode root) {
        if(root == null){
            return 0;
        }
        int left = maxDepth(root.left);
        int right = maxDepth(root.right);
        return Math.max(left,right)+1;
    }
}

leetcode 原题链接 可以打开测试下