bzoj 2733: [HNOI2012]永无乡（线段树启发式合并）

Description

永无乡包含 n 座岛，编号从 1 到 n，每座岛都有自己的独一无二的重要度，按照重要度可 以将这 n 座岛排名，名次用 1 到 n 来表示。某些岛之间由巨大的桥连接，通过桥可以从一个岛 到达另一个岛。如果从岛 a 出发经过若干座（含 0 座）桥可以到达岛 b，则称岛 a 和岛 b 是连 通的。现在有两种操作：B x y 表示在岛 x 与岛 y 之间修建一座新桥。Q x k 表示询问当前与岛 x连通的所有岛中第 k 重要的是哪座岛，即所有与岛 x 连通的岛中重要度排名第 k 小的岛是哪 座，请你输出那个岛的编号。 
 

Input

输入文件第一行是用空格隔开的两个正整数 n 和 m，分别 表示岛的个数以及一开始存在的桥数。接下来的一行是用空格隔开的 n 个数，依次描述从岛 1 到岛 n 的重要度排名。随后的 m 行每行是用空格隔开的两个正整数 ai 和 bi，表示一开始就存 在一座连接岛 ai 和岛 bi 的桥。后面剩下的部分描述操作，该部分的第一行是一个正整数 q， 表示一共有 q 个操作，接下来的 q 行依次描述每个操作，操作的格式如上所述，以大写字母 Q 或B 开始，后面跟两个不超过 n 的正整数，字母与数字以及两个数字之间用空格隔开。 对于 20%的数据 n≤1000,q≤1000 
 
对于 100%的数据 n≤100000,m≤n，q≤300000 
 

Output

对于每个 Q x k 操作都要依次输出一行，其中包含一个整数，表 示所询问岛屿的编号。如果该岛屿不存在，则输出-1。 
 

Sample Input

5 1
4 3 2 5 1
1 2
7
Q 3 2
Q 2 1
B 2 3
B 1 5
Q 2 1
Q 2 4
Q 2 3

Sample Output

-1
2
5
1
2

中文题，题意就不说了。

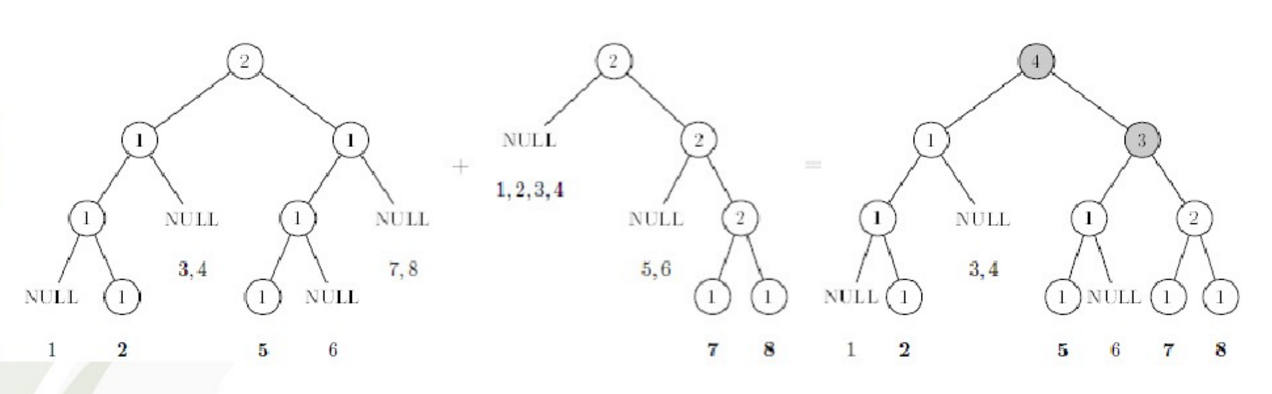
查询区间第k大的值可以用线段树，还有就是涉及到线段树的合并。

这题因为数值都是1~n，所以可以把出现的数字在线段树里的相应位置更新为1，查询的时候就类似于二分查找。

线段树合并的如下图所示：（图片转自黄嘉泰的ppt）

还有数组的大小要开比nlogn要大一些。

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>

using namespace std;

const int maxn = 100010;

int cnt;
int f[maxn];
int id[maxn],Rank[maxn];
int ls[maxn*18],rs[maxn*18],sum[maxn*18],root[maxn];


int find(int x)
{
    if(f[x] == x)
        return f[x];
    else
        return f[x] = find(f[x]);
}

void PushUp(int k)
{
    sum[k] = sum[ls[k]] + sum[rs[k]];
}
void update(int &k,int l,int r,int rk)
{
    if(k == 0)
        k = ++cnt;
    if(l == r)
    {
        sum[k] = 1;
        return;
    }
    int m = (l+r)/2;
    if(rk <= m)
        update(ls[k],l,m,rk);
    else
        update(rs[k],m+1,r,rk);
    PushUp(k);
}

int query(int k,int l,int r,int rk)
{
    if(l == r)
        return l;
    int res;
    int m = (l+r)/2;
    if(sum[ls[k]] >= rk)
        res = query(ls[k],l,m,rk);
    else
        res = query(rs[k],m+1,r,rk-sum[ls[k]]);
    return res;
}

int Merge(int x,int y)
{
    if(x == 0)
        return y;
    if(y == 0)
        return x;
    ls[x] = Merge(ls[x],ls[y]);
    rs[x] = Merge(rs[x],rs[y]);

    sum[x] = sum[ls[x]] + sum[rs[x]];

    return x;
}

void init()
{
    cnt = 0;
    memset(sum,0,sizeof(sum));
    memset(root,0,sizeof(root));
    memset(ls,0,sizeof(ls));
    memset(rs,0,sizeof(rs));
}


int main(void)
{
    int n,m,q,i,j;
    while(scanf("%d%d",&n,&m)==2)
    {
        init();
        for(i=1;i<=n;i++)
        {
            scanf("%d",&Rank[i]);
            id[Rank[i]] = i;
        }
        for(i=1;i<=n;i++)
            f[i] = i;
        for(i=1;i<=m;i++)
        {
            int x,y;
            scanf("%d%d",&x,&y);
            int tx = find(x);
            int ty = find(y);
            if(tx != ty)
                f[tx] = ty;
        }
        for(i=1;i<=n;i++)
            update(root[find(i)],1,n,Rank[i]);
        scanf("%d",&q);
        while(q--)
        {
            int x,k;
            char op[5];
            scanf("%s%d%d",op,&x,&k);
            if(op[0] == 'B')
            {
                int tx = find(x);
                int ty = find(k);
                if(tx != ty)
                {
                    root[tx] = Merge(root[tx],root[ty]);
                    f[ty] = tx;
                }
            }
            else
            {
                int tx = find(x);
                if(sum[root[tx]] < k)
                {
                    printf("-1\n");
                    continue;
                }
                int t = query(root[tx],1,n,k);
                printf("%d\n",id[t]);
            }
        }
    }

    return 0;
}