本文详细探讨了数据结构中的最优二叉树，即哈夫曼树，介绍了其带权路径长度最短的特性及求解步骤。此外，还讲解了树和森林的存储方法，包括双亲表示法、孩子表示法和孩子兄弟结点表示法。接着，文章讨论了查找二叉树，特别是二叉排序树和平衡二叉树的概念。对于图，讲解了无向图、有向图、完全图和连通图的概念，以及图的存储方式如邻接矩阵和邻接链表，并涉及最小生成树的普里姆算法和克鲁斯卡尔算法。最后，提到了图的拓扑序列在有向图中的应用。
数据结构
最优二叉树
最优二叉树又称哈夫曼树，是一类带权路径长度最短的树。
路径：树中一个结点到另一个结点之间的通路。
结点的路径长度：路径上的分支数
树的路径长度：根结点到达每一个叶子结点之间的路径长度之和
权：结点代表的值
结点的带权路径长度：该结点到根结点之间的路径长度乘以该结点的权值
树的带权路径长度（树的代价）：树的所有叶子结点的带权路径长度之和
哈夫曼树的求法：给出一组权值，将其中最小的两个权值作为叶子结点，其和作为父结点，组成二叉树，然后删除这两个叶子结点权值，将父结点的值添加到这组权值中。重复上述步骤，直至所有权值结点都使用完。
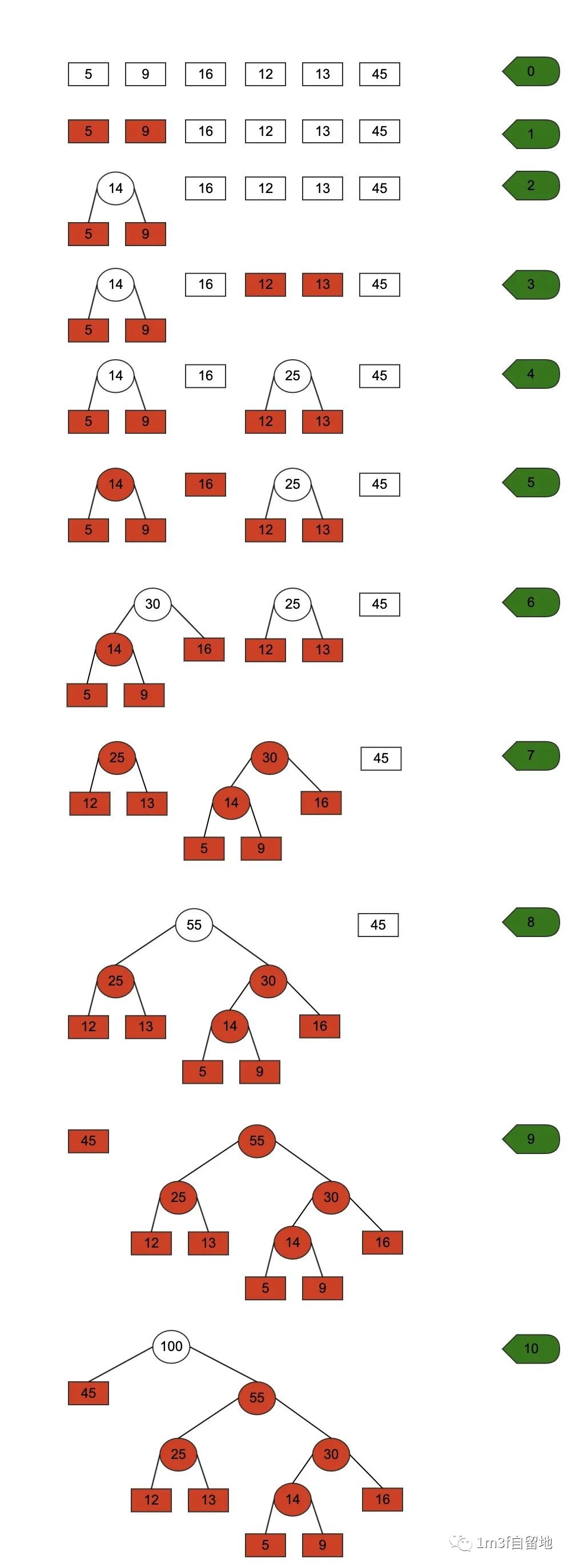
最优二叉树求解步骤
树和森林
双亲表示法：用一组连续的地址单元存储树的结点，并在每个结点中附带一个指示器，指出其双亲结点所在数据元素的角标。
孩子表示法：在存储结构中用指针指示出结点的每个孩子结点，为树中每个结点的孩子建立一个链表。
孩子兄弟结点表示法：二叉链表表示法，为每个存储结点设置两个指针域，分别指向该结点的第一个孩子和下一个兄弟结点。
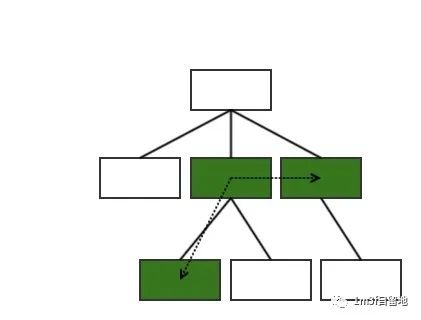
孩子兄弟结点表示法
树和二叉树的转换：
树的最左边结点作为二叉树的左子树，其他兄弟结点作为该左子树的右子树结点。
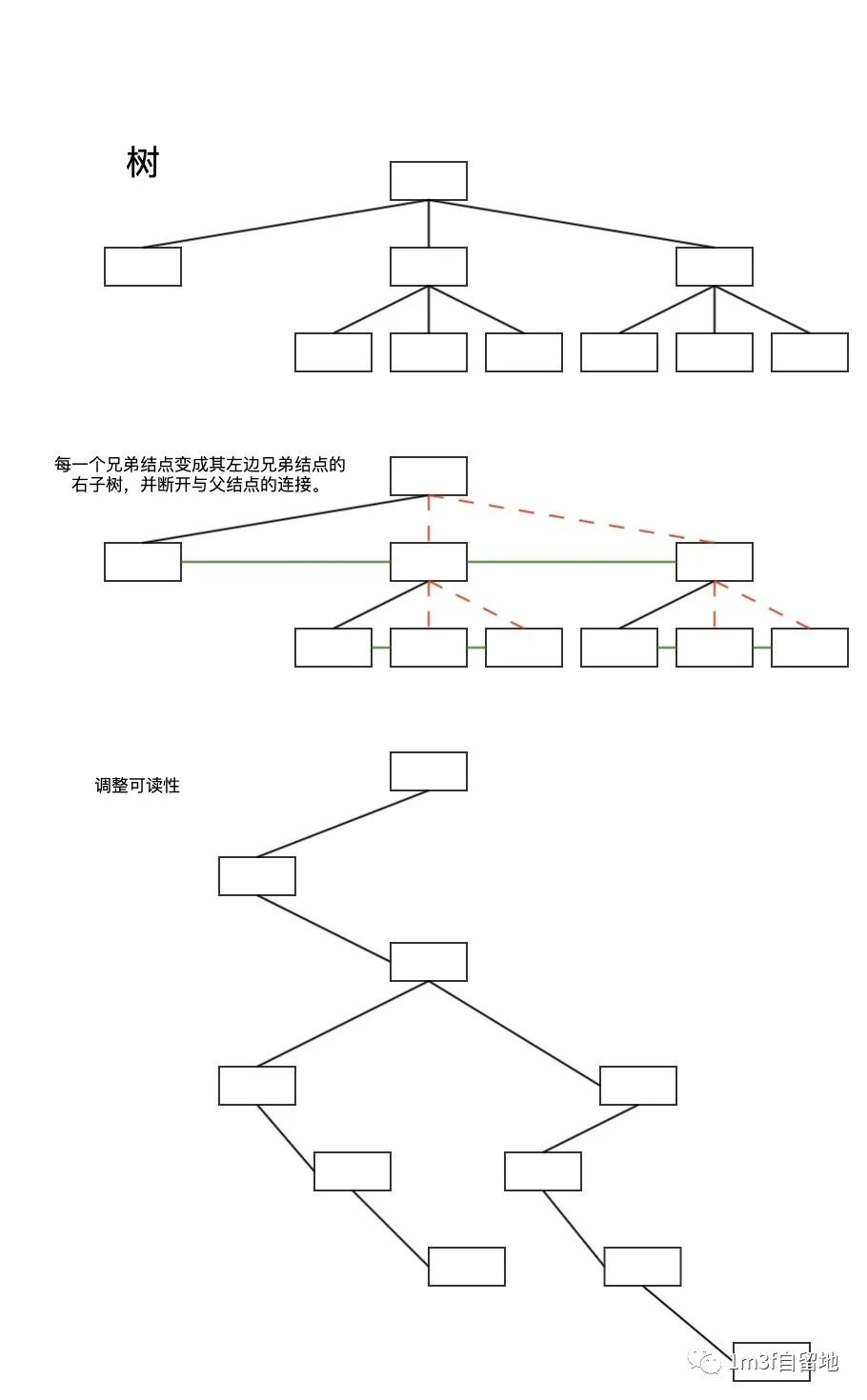
树和二叉树的转换
查找二叉树
查找二叉树（二叉排序树）上每个结点都存储一个值，且每个结点的左孩子结点值都小于父结点的值，每个右孩子结
最低0.47元/天 解锁文章
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
