数据结构与算法专题之图——图的基本定义与存储

本文链接：https://blog.csdn.net/ShannonNansen/article/details/77302925

　　本章我们开启一个全新的世界——图。这里的图不是我们日常理解的jpg，而是一种网状的拓扑结构。图在我们日常生活中应用相当广泛，比如我们常用的地图导航，如何找到出发点到目的地的最短路线？次短路线？最优选择？其中就包含了对图结构的各种算法处理。图论不光能解决直观的路径问题，甚至可以用来求解方程式、解决工程生产问题等，应用相当广泛，如果说树是最重要的数据结构，那么图则是最实用的数据结构。

　　通过之前对树的学习，我们应该已经学会的非线性数据结构的基本存储方式。下面我们先介绍一下关于图的一些基本概念。

图的基本概念

定义

　　图是由顶点集合与顶点间关系（边）集合所构成的一种数据结构。我们写作G=(V, E)，其中V代表顶点（Vertex）的非空有穷集合，E代表边（Edge）的非空有穷集合。

类型

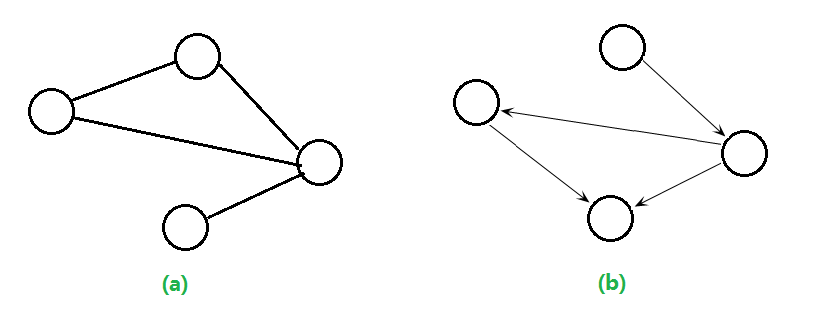
　　图的基本类型有两种：有向图和无向图。顾名思义就是图上的边是否有表示方向的顺序关系，如下图，a为无向图，b为有向图。

　　为了便于理解，我们可以认为无向图是一种特殊的有向图，我们认为无向图的每一条边都是具有两个方向的有向边，这样便于对后边图的存储的理解。

其他概念

　　1. 图上两点之间路径不唯一。

　　2. 对于图上任意两点都可以连通的图叫做连通图。

　　3. 图的边是可以带权值的，一般代表路径长度。

　　4. 图顶点的度：对于无向图来说，顶点的度就是其直接相邻的点的个数；对于有向图来说，顶点的度分为入度和出度，分别代表可直接到达的点的数量和可直接到达它的点的数量。如上图b中最右边的点的出度为2，入度为 1。

　　5. 按照边的数量多少分为稀疏图和稠密图，应用中要根据图的稠密程度来使用不同的算法解决问题。

图的存储

　　上面提到根据边的数量，图可以分为稀疏图和稠密图，根据不同的图，我们有不同的存储方式，我们常用的有两种：邻接矩阵和邻接表。

邻接矩阵

　　邻接矩阵就是用二维数组表示的点与点之间的关系，通常适用于顶点数较少的图。

　　假设图G是一个具有n个顶点的无向图，则邻接矩阵为n*n的矩阵，如下图定义：

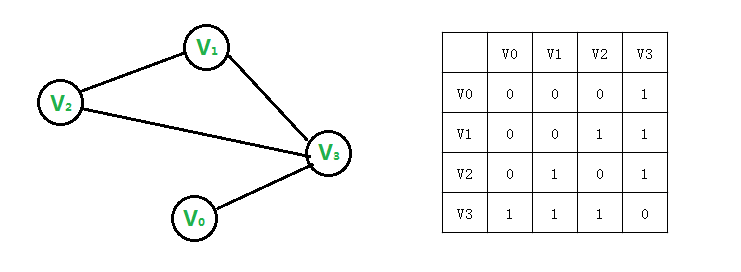
　　如下图，无向图G与其邻接矩阵：

　　观察上图可以看出，无向图的邻接矩阵是一个关于对角线对称的矩阵，我们有了这个矩阵，就可以知道下面这些事情：

　　1. 任意两点之间有没有边相连，比如我想知道vi和vj是否直接相连，对于无向图来说，只需查看数组arr[i][j]或者arr[j][i]是否为1即可。

　　2. 顶点的度。我们也可以计算出某一点的度，对于某一个顶点，只需计算邻接矩阵中对应行或者列的1的数量即可，例如v2的度为2。

　　3. 获取邻接点。对于顶点Vi，只需遍历矩阵中第i行所有元素，若有arr[i][j]==1，则说明Vj为Vi的一个邻接点。

　　当然对于有边权的图来说，只需把矩阵中的1改为对应的值即可。另外需要注意的是，我们上面用0代表无边（不可达），若边权值有0存在，则我们需要使用另外的整数来表示点与点不可达，通常我们用正无穷（∞）来表示，当然计算机中没有正无穷，我们通常使用一个大于最大边权的值，一般是一个较大的int（0x7f7f7f7f），来表示不可达。

　　对于有向图来说，与无向图的区别就是矩阵不会关于对角线对称，原因是两点之间，可能是一条单向的边，比如Vi和Vj之间只有一条Vi指向Vj的边，则arr[i][j] = 1，而arr[j][i] = 0，因为并没有Vj指向Vi的边，所以矩阵不会对称。现在反观无向图，其实相当于有边关系的两点之间是有一条双向的边。

　　关于邻接矩阵，是一个很简单的图的存储方式，只需要一个二维数组即可将图存储。下面给出代码：

const int MAX_P = 1010; // 最大点数量
const int NO_PATH = 0x7f7f7f7f; // 定义不可达的边权值
int G[MAX_P][MAX_P];

void init() // 初始化图
{
    memset(G, 0x7f, sizeof(G));
}

void addEdge(int i, int j, int w) // 添加一条i->j权值为w的边
{
	G[i][j] = w;
}

bool isConnection(int i, int j) // 检查是否有直接i->j的边
{
	return G[i][j] != NO_PATH;
}

邻接表

　　对于一个稀疏图来说，使用邻接矩阵存储太浪费内存空间了，如果一个含有100个顶点的图，对于V0来说，只有V4和V6两个邻接点，那么仅邻接矩阵的第一行就浪费掉了98个存储单元，空间消耗是巨大的。所以对于点较多而边较少的稀疏图，我们引入了邻接表。

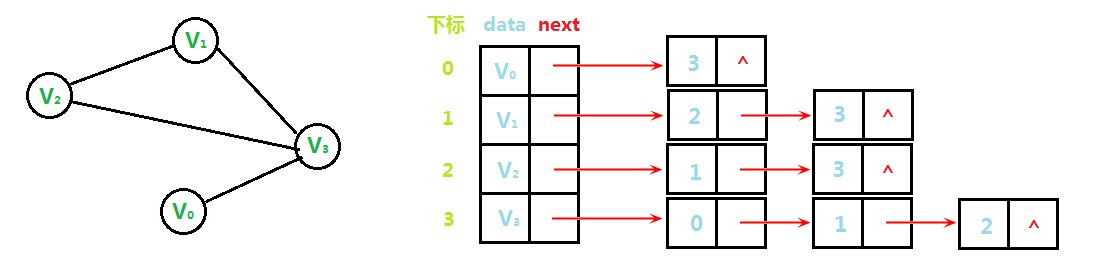
　　我们将图的所有顶点存入到一个一维数组中，数组中每个元素都对应着一个链表，链表每个元素都代表了该点的邻接点，如下图：

　　为什么使用链表呢？不难看出，每个顶点的邻接点数量都不确定，而链表恰好可以动态地添加或删除元素。

　　通过上图，我们可以看出，所谓的一维数组其实就是一组链表的头结点，每个头结点都代表了图的一个顶点，对于每个头结点都对应了一个链表，链表中每个元素都是该点的一个邻接点，也代表了该点到邻接点有一条单向边（弧）。当然上图中没有体现出边的权值，链表的数据域存储的是邻接点的编号，若要用邻接表存储带权图，只需要为链表的结点增加一个数据域来存储权值即可。

　　代码实现起来也是很简单的，我们定义好结点的结构，根据图顶点的数量声明一组头结点，然后再根据图的边依次为各顶点添加邻接点即可。至于为什么要把头结点声明成数组的形式，是因为我们可以方便地通过数组下标来找到对应顶点的头结点，从而找到相应的链表来进行一系列操作。代码如下：

const int MAX_P = 1010;

struct node
{
	int idx, w; // 分别代表邻接点边号和边的权值
	node *next;
};

node G[MAX_P]; // 声明一个头结点数组

void init(int n) // 初始化n个顶点的图
{
	for(int i = 0 ; i <= n ; i++)
	{
		G[i].next = NULL; 
		// 这里是初始化链表，注意我们声明的是头结点数组，并不是指针 
		// 在图使用完毕后记得像链表一样释放内存
	}
}
void addEdge(int u, int v, int w) // 添加一条u->v权值为w的边
{
	node *head = &G[u]; // 获取u对应的头结点的指针
	node *p = new node;
	p->idx = v; // 邻接点编号
	p->w = w; // 边的权值
	// 为了方便，我们使用头部插入
	p->next = head->next;
	head->next = p;
}
bool isConnection(int u, int v) // 判断u->v边是否存在
{
	node *head = &G[u];
	node *p = head->next;
	while(p)
	{
		if(p->idx == v)
			return true;
	}
	return false;
}

　　可以看出，邻接表只不过是一组链表而已，它与邻接矩阵的区别是，邻接表的第二维度的长度是不确定的，可以动态地增减。我们在操作的时候只需要拿到头结点指针，即可像单链表一样操作了。

使用STL vector实现邻接表

　　前面提到使用链表来实现邻接表的原因，是因为链表可以动态地增加元素，整个链表的长度是不定的，那么也就是说，完全可以找到一种数据不定长的容器来代替链表从而实现邻接表。很幸运，C++ STL为我们提供了这样一种容器——Vector

　　Vector，向量，泛型容器，相当于是一个动态的数组，不定长的数组，与我们的链表极为相似，只不过C++STL对其进行了封装，使其可以像数组一样通过[]访问下标来访问vector内的元素，使用起来相当地方便，下面我们就用vector来实现邻接表，在今后图论的学习中，除特殊情况，基本上代码都会采用vector式的邻接表。

　　vector的使用相当方便，只需要这样：

vector<int> arr;

　　即可声明一个初始为空的int型数组，可以通过调用arr.push_back();来向数组尾部添加元素从而动态地扩展数组的大小。可以通过调用arr.size();来获取不定长数组当前的长度，也可以通过arr[i]来访问不定长数组的第i个元素（下标也是从0开始的）。

　　由于不定长数组与数组一样，每个元素只能存储一个值，所以如果我们的图是带权图，则需要两个数值（二元组）来存储一个邻接点（点编号、权值），由于我们的vector是泛型，所以我们可以定义一个含有两个数据域的结构体，并将vector的泛型声明为该结构体类型，如下：

struct node
{
	int idx, w;
};

vector<node> G[MAX_P];

　　为了简便，我们下面的实现就假设图没有权值，就单纯地存储点与点之间的边关系，那么我们就可以这样实现邻接表：

const int MAX_P = 1010;

vector<int> G[MAX_P];

void init(int n) // 初始化n个顶点的图
{
	for(int i = 0 ; i <= n ; i++)
	{
        	G[i].clear(); // 清除不定长数组的所有元素，即初始化，置空
	}
}

void addEdge(int u, int v) // 添加一条u->v边
{
	G[u].push_back(v);
}

bool isConnection(int u, int v)
{
	int len = G[u].size();
	for(int i = 0 ; i < len ; i++)
	{
        	if(G[u][i] == v)
			return true;
	}
	return false;
}

　　是不是这样就简单了好多？可以像数组一样用下标操作“链表”。