矩形覆盖面积

Stay--hungry

已于 2022-06-21 20:19:53 修改

阅读量1.2k

点赞数 1

分类专栏： # 线段树文章标签：算法

于 2022-06-20 17:38:05 首次发布

本文链接：https://blog.csdn.net/Shao_yihao/article/details/125361659

版权

线段树专栏收录该内容

1 篇文章

订阅专栏

原题链接

题目大意： 在标准直角坐标系中，若干个矩形区域被涂上了油漆（注意：矩形间可能重叠）。矩形的表示方式为 $x_1,y_1,x_2,y_2)$ ，代表矩形的两个对角点的坐标。求被油漆覆盖的区域一共有多大面积。

关键字：线段树、扫描线法
（本题是线段树非常特殊的一种应用。）

$n$ 个矩形，竖边有 $2 n$ 个。每个竖边可以用四个参数 $x,y_1,y_2,st)$ 来描述，其中 $s t$ 用来区分同一个矩形中的两条边，反映的是该边的性质（入边 or 出边）。

struct Segment
{
    int x, y1, y2;
    int st; //反映该线段的性质：+1表示入边，-1表示出边
    bool operator< (const Segment &s)const //横坐标作为排序标准
    {
        return x < s.x;
    }
}seg[N * 2];

读入 $n$ 个矩形实际上就是读入这 $2 n$ 个线段：

int n;
cin >> n;
for (int i = 0, t = 0; i < n; i ++)
{
	int x1, y1, x2, y2;
    cin >> x1 >> y1 >> x2 >> y2;
    seg[t ++] = {x1, y1, y2, +1}; seg[t ++] = {x2, y1, y2, -1};
}
sort(seg, seg + 2 * n); //根据横坐标对这2n个线段进行排序

在这里插入图片描述

扫描线法即以这 $2 n$ 个线段为基础，生成 $2 n$ 个扫描线（可能存在重合），每根直线上实际用到的长度即矩形的高，相邻扫描线之间的距离即矩形的长，从而可以求出这两扫描线之间矩形的面积。将所有面积累加起来，即得最终总面积。

$S_1=(seg[1].x-seg[0].x)\cdot h_1\\S_2=(seg[2].x-seg[1].x)\cdot h_2\\ \vdots\\S_i=(seg[i].x-seg[i-1].x)\cdot h_i$ $S_总=S_1+S_2+\cdots+S_{2n-1}$ 例如：
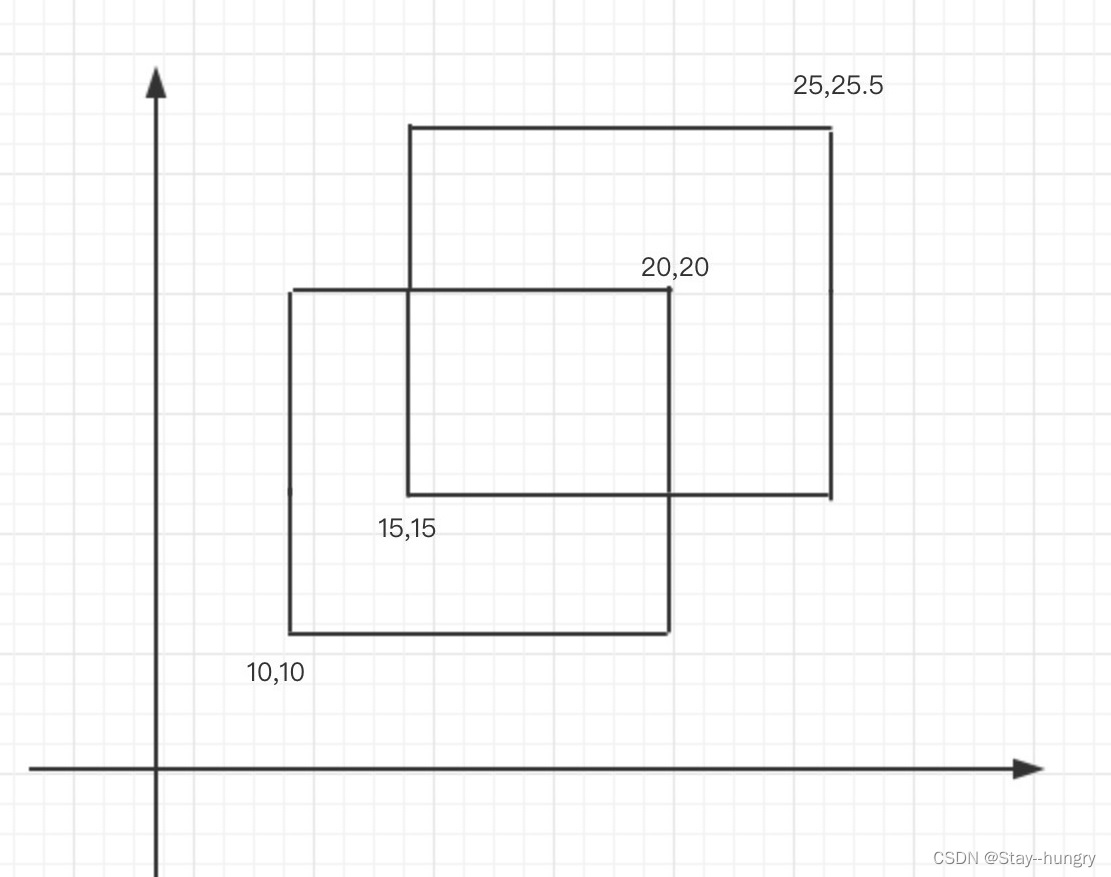
在这里插入图片描述
转化为计算：

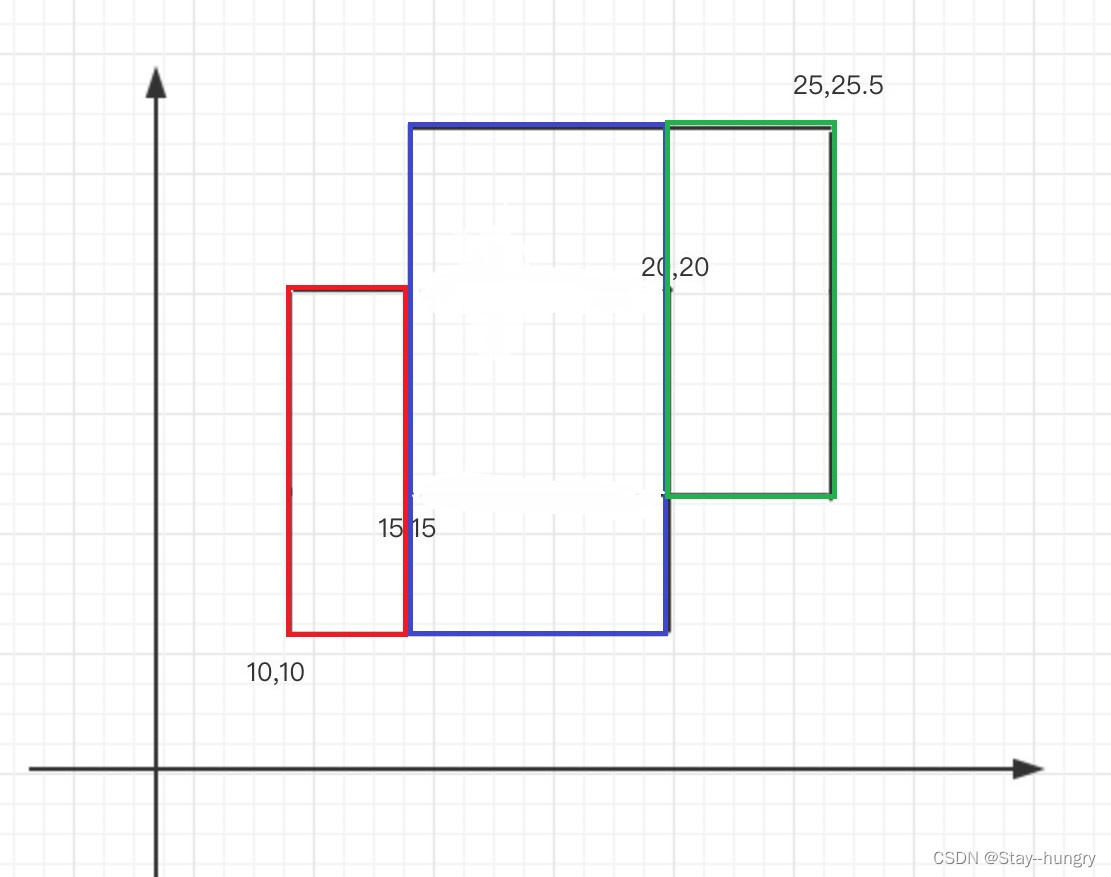
这种方法的好处是：只需要从左往右扫，一步一更新即可。每次计算需要知道的信息有：

每个新矩形的的高度。
每个新矩形的宽度。

其中每个新矩形的宽度非常容易计算，只需要将扫描线进行排序，相邻扫描线相减即可求得。

而每个新矩形高度的计算则比较麻烦，因为扫描线上实际用到的长度受先前所枚举的扫描线的影响。

具体分析如下：
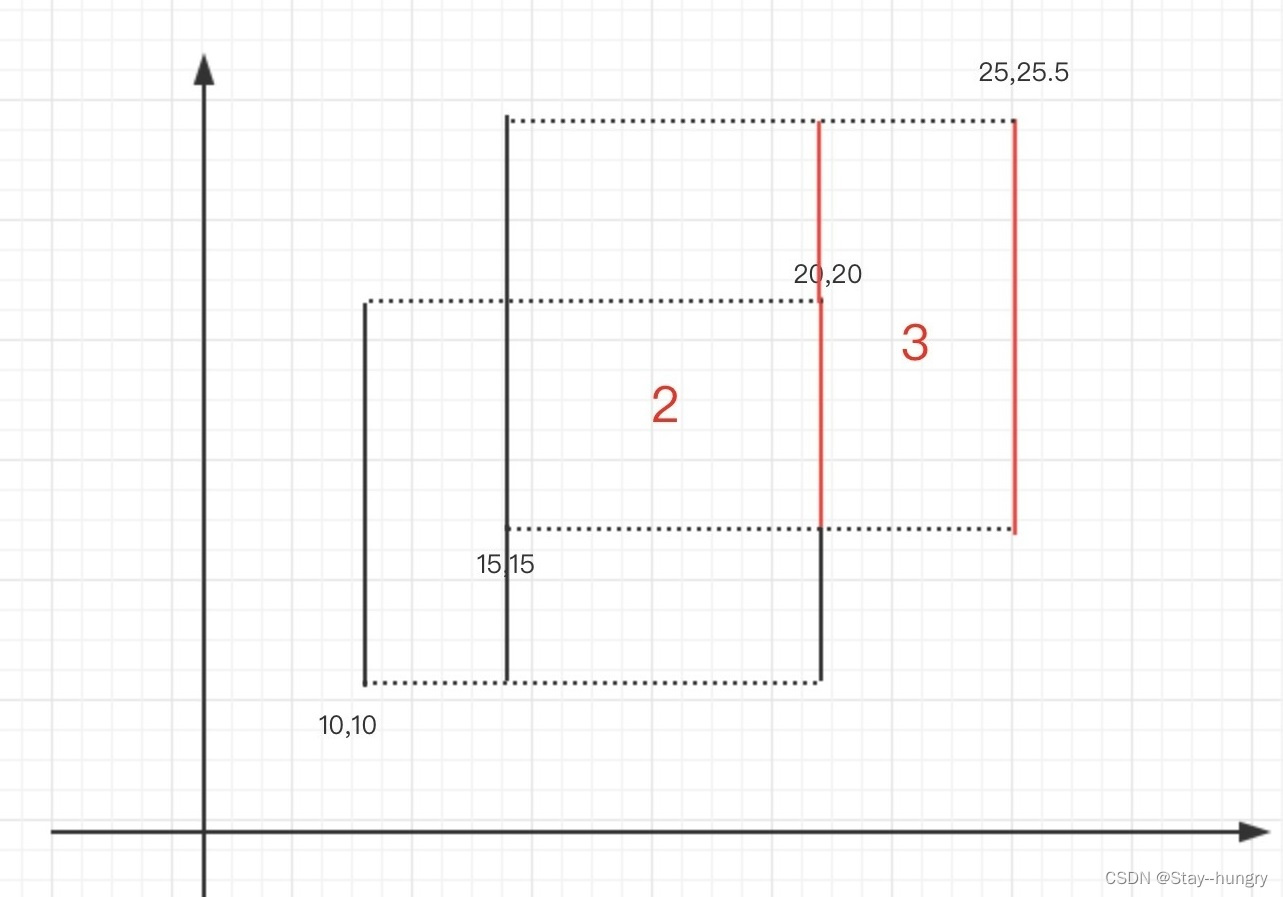
在这里插入图片描述
首先问一个问题：②号矩形的高如何计算？
很直观的回答就是： $10 + (25.5 - 20) = 15.5$ ，先算上①号矩形高，再加上②号矩形多出来的部分。
那③号矩形的高如何计算？
显然， $15.5 - (15 - 10) = 10.5$ ，先用②号矩形的高那部分减去多出来的部分。

那么为什么有时候 “多出来” 是加上一个值，有时候 “多出来” 是减掉一个值呢？
这个问题是扫描线法最核心的问题 —— “入边” 和“出边” 的问题。

定义一个矩形中，左侧的高为“入边”，右侧的高为“出边”。

其实所谓的从左往右（也可以是从上往下），就是扫描的方向。

当从左往右扫，遇到入边扫描线，则对入边区间进行 $+ 1$ ，遇到出边扫描线，就对出边区间进行 $- 1$ ，这就是加入区间或减去区间的规律。

这其实是一种差分的思想，不断更新每个小区间被覆盖的次数，整体上，所有覆盖次数 $\ge 1$ 的小区间构成了当前矩形的高。

具体实现方面，按横坐标的大小枚举扫描线，为保证计算时使用的是最新的实际长度，需要对整个区间进行动态维护，常用的方法是：线段树。

将整个区间以1个单位长度进行划分，线段树的每个底层结点都对应一个单位长度的区间。

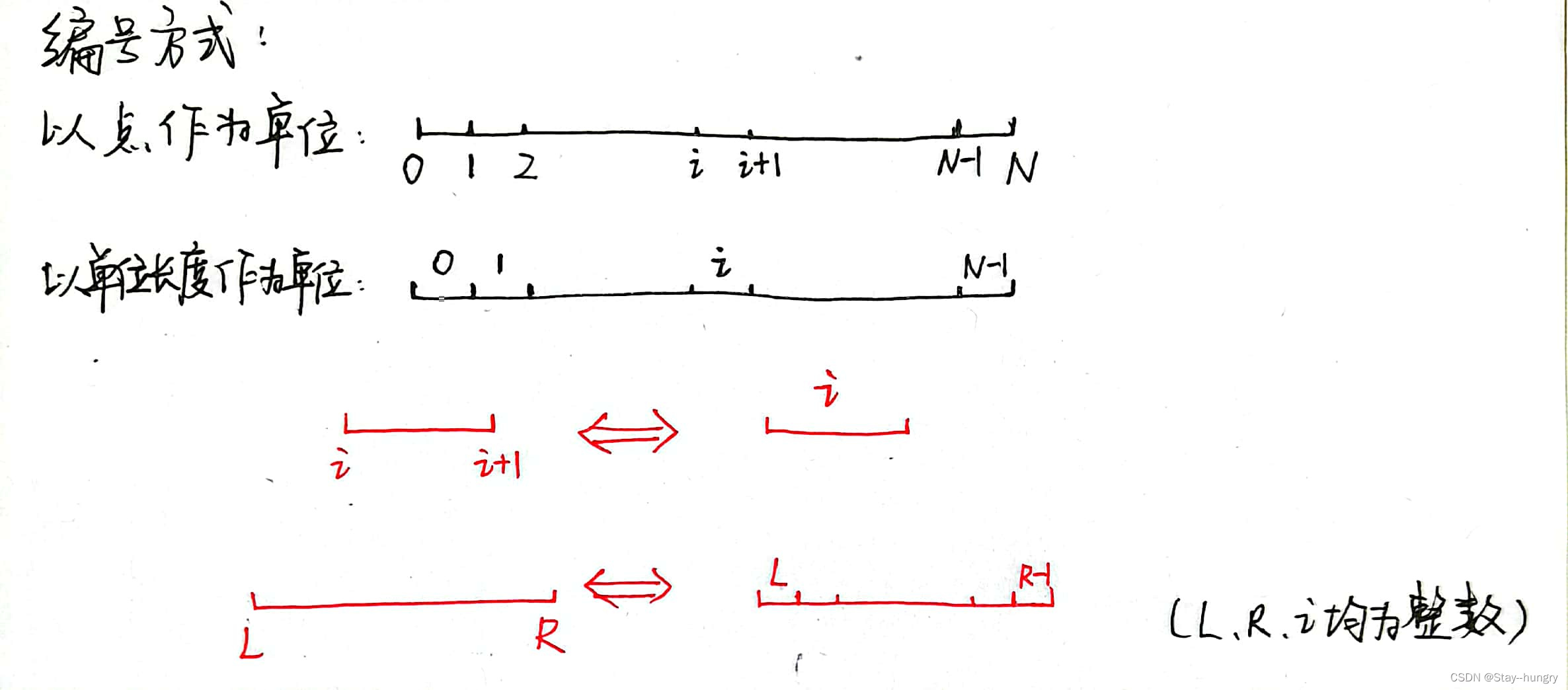
在这里插入图片描述
具体的存储结构为：

struct Node
{
    int l, r; //该结点对应的区间的边界单位区间（注意：并非端点，而是两端的单位区间！）
    int cnt;  //该结点对应的区间被覆盖的次数（完全覆盖）
    int len;  //该结点对应的区间被覆盖的长度
}tr[N * 4];

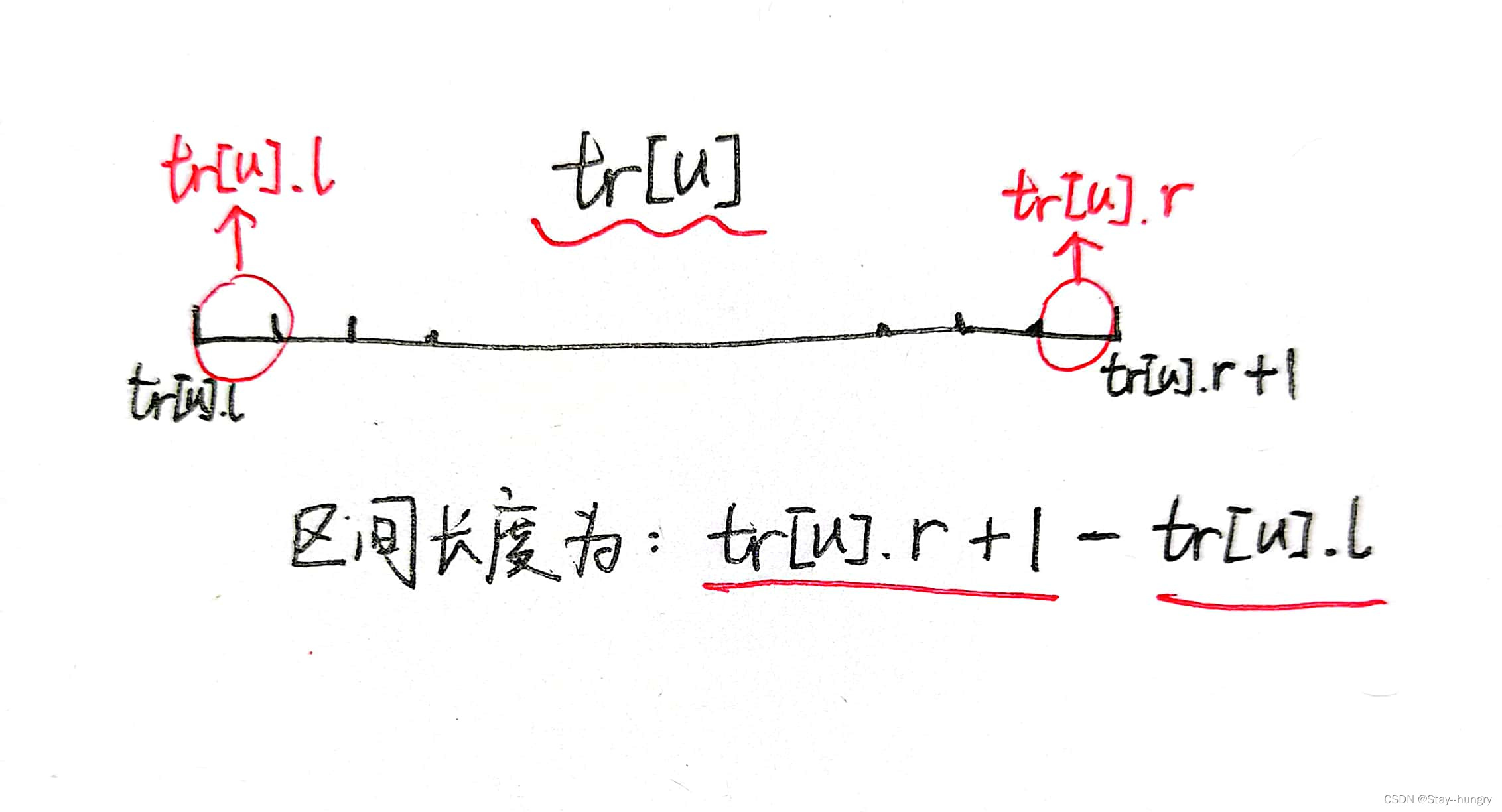
在这里插入图片描述
从而根结点tr[1]指向的是整个区间，tr[1].len始终反映的是当前区间的有效长度。

题目所给的编号方式为①，而线段树中则是按②进行存储。因此若向线段树中加入区间[seg[i].l, seg[i].r]，则更新操作为：modify(1, seg[i].l, seg[i].r - 1, st)。

#include <iostream>
#include <algorithm>
using namespace std;

const int N = 10010;
struct Segment
{
    int x, y1, y2;
    int st; //表示该线段的性质：入 or 出
    bool operator< (const Segment &t)const //根据横坐标进行排序
    {
        return x < t.x;
    }
}seg[N * 2];
struct
{
    int l, r; 
    int cnt;  
    int len;  
}tr[N * 4];

void build(int u, int l, int r)  //建立线段树，底层结点为单位长度的小区间
{
    tr[u] = {l, r}; //其余的属性（cnt、len）默认置为0

    if (l != r) //若可以再半分
    {
        int mid = (l + r) / 2;
        build(2 * u, l, mid), build(2 * u + 1, mid + 1, r);
    }
}

void pushup(int u) //更新结点信息
{
    if (tr[u].cnt > 0) tr[u].len = tr[u].r - tr[u].l + 1; //该区间被完全覆盖
    else 
    {
    	if (tr[u].l == tr[u].r) tr[u].len = 0; //该区间没有被完全覆盖，又是单位区间，因此该区间就是完全没被覆盖，即被覆盖的长度为0
    	else tr[u].len = tr[2 * u].len + tr[2 * u + 1].len; //该区间没有被完全覆盖，但子孙结点可能会被完全覆盖
    }
}
void modify(int u, int L, int R, int st) //更新线段树（加入或删除一个区间）
{
    if (L <= tr[u].l && tr[u].r <= R)  //完全包含
    {
        tr[u].cnt += st;
        pushup(u);
    }
    else
    {
        int mid = (tr[u].l + tr[u].r) / 2;
        if (L <= mid) modify(2 * u, L, R, st);
        if (R > mid) modify(2 * u + 1, L, R, st);
        pushup(u);
    }
}

int main()
{
    build(1, 0, 9999); //初始化线段树

    int n;
    cin >> n;
    for (int i = 0, t = 0; i < n; i ++)
    {
        int x1, y1, x2, y2;
        cin >> x1 >> y1 >> x2 >> y2;
        seg[t ++] = {x1, y1, y2, +1}; seg[t ++] = {x2, y1, y2, -1};
    }
    sort(seg, seg + 2 * n); //根据横坐标进行排序

    int res = 0;
    for (int i = 0; i < 2 * n; i ++)
    {
        if (i > 0) res += tr[1].len * (seg[i].x - seg[i - 1].x); //从第2条线开始算
        modify(1, seg[i].y1, seg[i].y2 - 1, seg[i].st); //加入（或删除）一个区间（根据k而定）
    }
    cout << res;

    return 0;
}