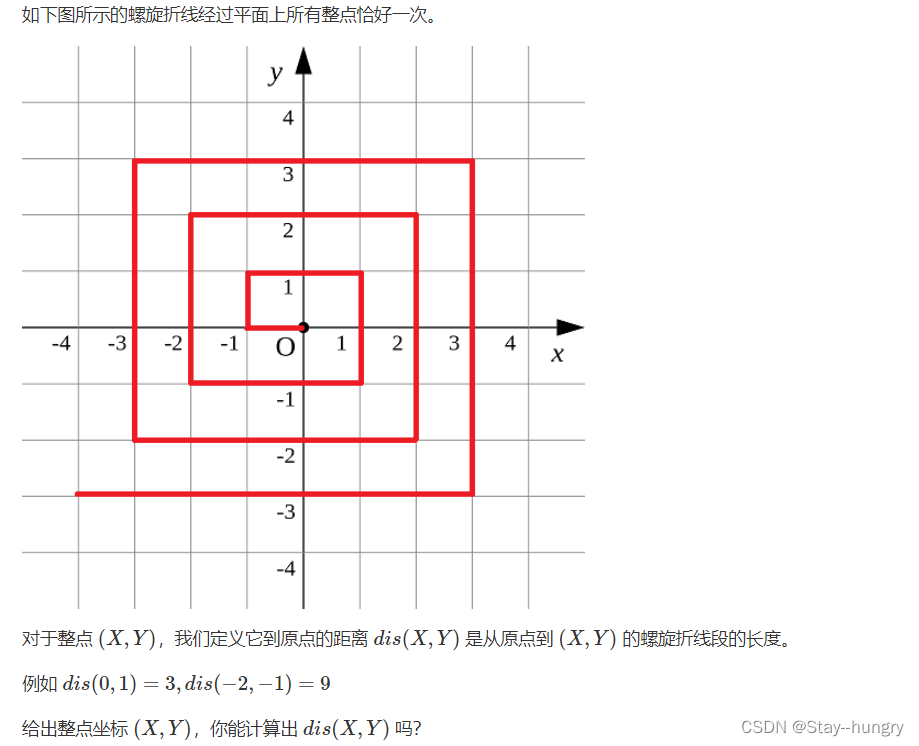
思路:
-
对于点 A ( x , y ) A(x,y) A(x,y),首先判断出该点属于上下左右哪个区域
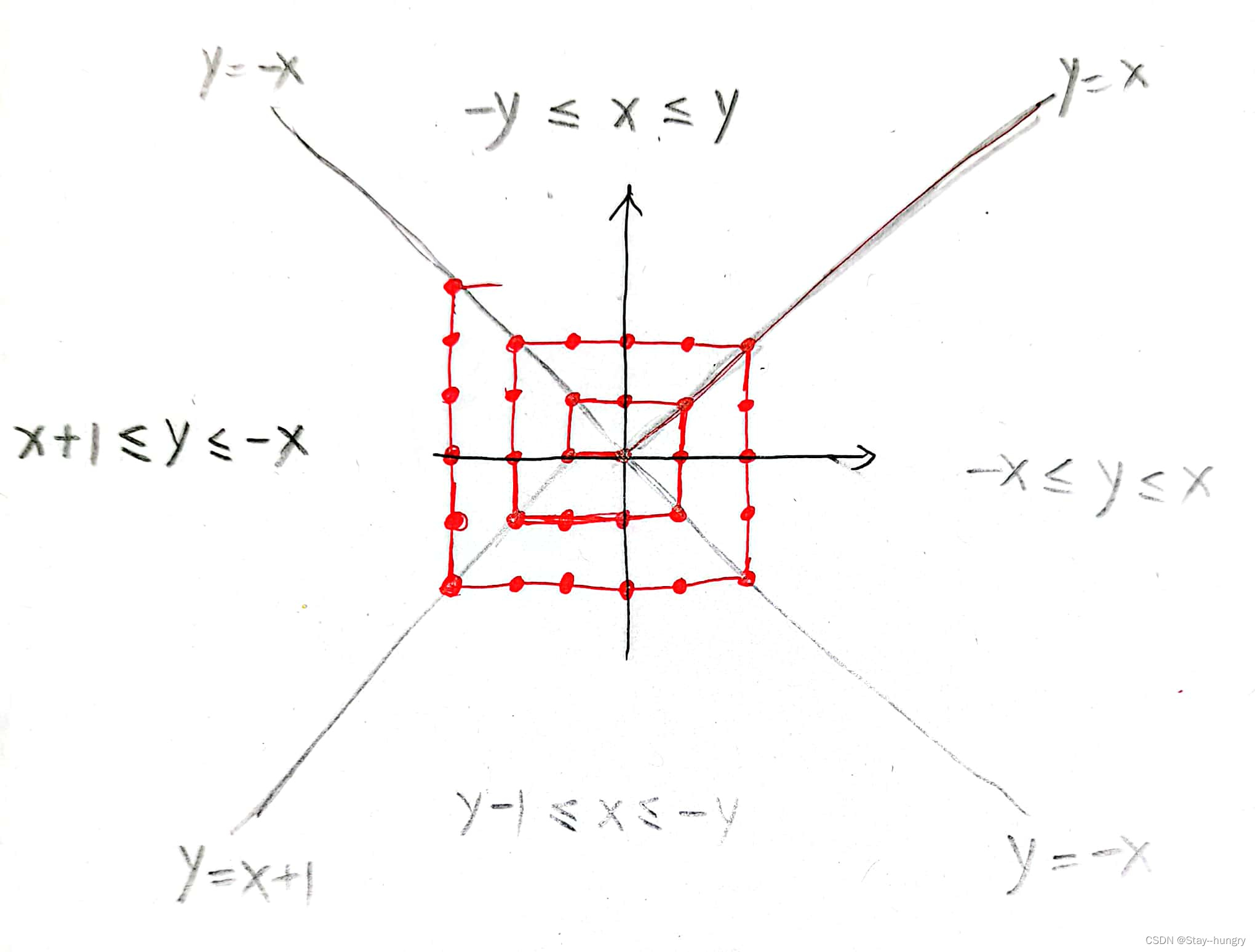
-
再求出该点所在“射线”的端点 B ( a , b ) B(a,b) B(a,b)(找出端点坐标与 ( x , y ) (x,y) (x,y)之间的关系)
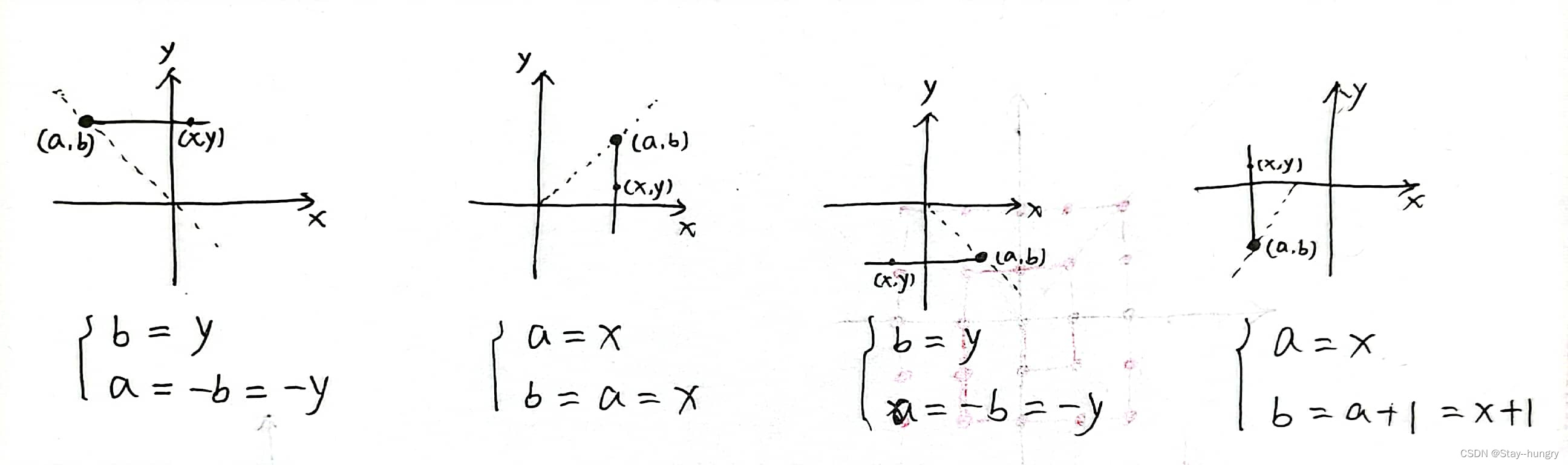
-
找规律,求出 B B B到原点的距离 ∣ B O ∣ |BO| ∣BO∣
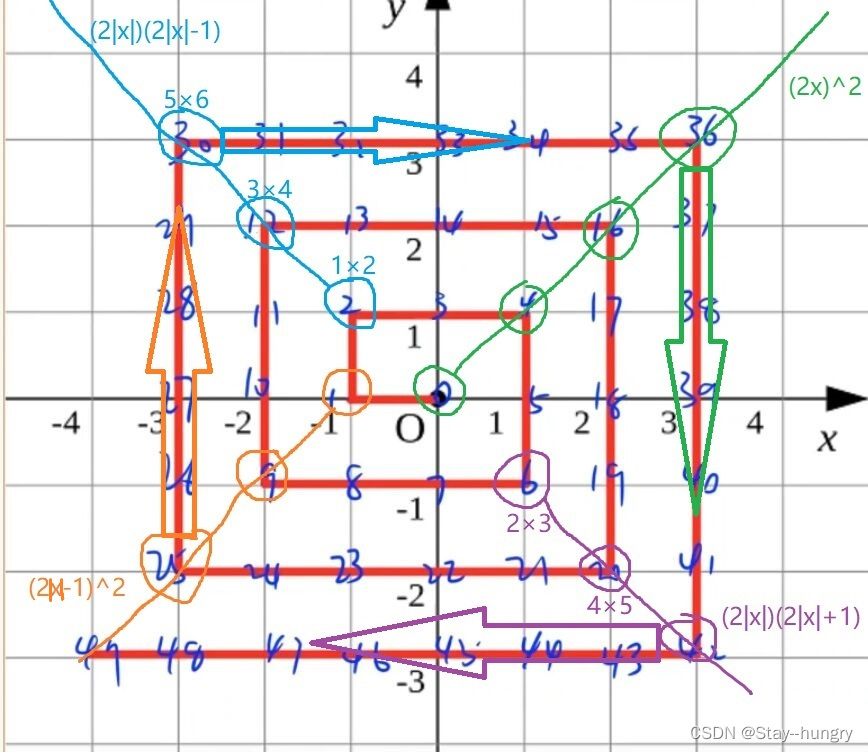
-
求 ∣ A O ∣ |AO| ∣AO∣转化为: ∣ A O ∣ = ∣ B O ∣ + ∣ A B ∣ |AO|=|BO|+|AB| ∣AO∣=∣BO∣+∣AB∣
#include <iostream>
using namespace std;
typedef long long LL;
int main()
{
int x, y;
cin >> x >> y;
int a, b; //射线的端点坐标
LL d; //端点到原点的距离
if (-y <= x && x <= y) // 在上方
{
a = -y, b = y;
d = (LL)2 * abs(a) * (2 * abs(a) - 1);
cout << d + x - a;
}
else if (-x <= y && y <= x) // 在右方
{
a = x, b = x;
d = (LL)2 * a * 2 * a;
cout << d + b - y;
}
else if (y - 1 <= x && x <= -y) // 在下方
{
a = -y, b = y;
d = (LL)2 * abs(a) * (2 * abs(a) + 1);
cout << d + a - x;
}
else // 在左方
{
a = x, b = x + 1;
d = (LL)(2 * abs(a) - 1) * (2 * abs(a) - 1);
cout << d + y - b;
}
return 0;
}



























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








