高精度算法简介
在C++中当你用int、long long,甚至是unsigned long long 都无法处理的超级巨大数字,你会感到无比痛苦甚至到绝望,那么我们此时就只有一种方法了——高精度算法。
高精度算法:属于处理大数字的数学计算方法,是用计算机对于超大数据的一种模拟加,减,乘,除等运算。对于非常庞大的数字无法在计算机中正常存储,于是,将这个数字拆开,拆成一位一位的存储到一个数组中, 用一个数组去表示一个数字,这样这个数字就被称为是高精度数。
结构体解法
在这里,我们将每个高精度数存为一个结构体就叫BigInt好了,里面最主要的有两个变量:(PS:请务必已经掌握结构体)
1)num[ ]负责记录数字的每一位(num[1]代表个位,num[2]代表十位,num[3]代表百位…)。
2)len负责记录这个数的位数。
这里M为这个数位数的上限。
(PS:static int x 是让所有的高精度数都共用这一个变量,比如说我在第一个高精度数中改变了这个量,那么在剩下的高精度数中就都改变了这个量,可以看作是全局变量,只不过只能在这种结构体里使用而已,在此主要目的是为了优化一下空间,并且使BigInt结构体能够独立)。
接下来给一个初值0,并就连着一起建个清零函数。
结构体不同部分的思路:
-
读入思路:先按字符数组读进来,再倒着装进int数组里。
-
输出思路:倒着输出。
-
比较运算思路(以小于号为例):
1)比较位数len。
2)一位一位num的去比较。
3)还不行…就相等了。 -
加法思路:一位一位的加,然后进位。
每次让S.num[i] += num[i] + A.num[i];(记住一定是+=,因为S.num[i]可能因上一位的进位而变为1了)。
接着判断如果S.num[i]是两位数了,即大于等于10,就进位:让S.num[i] -= 10,S.num[i + 1]++。 -
减法思路:一位一位的减,然后借位。
每次让S.num[i] += num[i] - A.num[i];
接着判断如果S.num[i]小于0了,就向高一位借1:让S.num[i] += 10,S.num[i + 1]–。 -
乘法思路:一位一位的去相乘,之后进位
假设要让this的第i位与A的第j位相乘:
举个例子,条件如下表,
可以知道this.num[5] * A.num[3]加在了第7位,即(3 + 5 - 1)位。
经推导可知this.num[i] * A.num[j]加在了第(i + j - 1)位
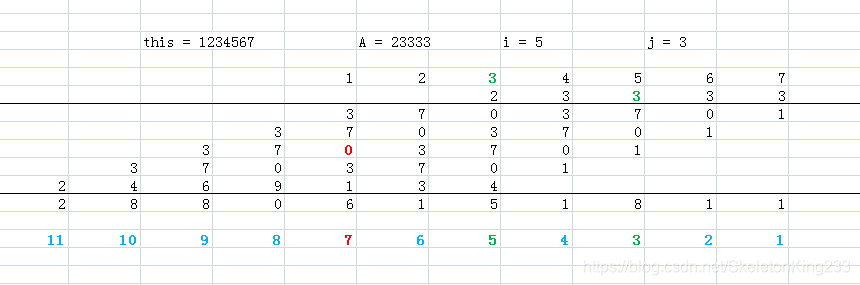
这样每次让S.num[i + j - 1] += num[i] * A.num[j],之后再进位就行了。
接下来就是结构体形式的代码了。
# include <cstdio>
# include <iostream>
# include <cstring>
# include <algorithm>
# include <cmath>
using namespace std;
# define FOR(i, a, b) for(int i = a; i <= b; i++)
# define _FOR(i, a, b) for(int i = a; i >= b; i--)
struct BigInt
{
static const int M = 1000;
int num[M + 10], len;
BigInt() { clean(); }
void clean(){
memset(num, 0, sizeof(num));
len = 1;
}
void read(){
char str[M + 10];
scanf("%s", str);
len = strlen(str);
FOR(i, 1, len)
num[i] = str[len - i] - '0';
}
void write(){
_FOR(i, len, 1)
printf("%d", num[i]);
puts("");
}
void itoBig(int x){
clean();
while(x != 0){
num[len++] = x % 10;
x /= 10;
}
if(len != 1) len--;
}
bool operator < (const BigInt &cmp) const {
if(len != cmp.len) return len < cmp.len;
_FOR(i, len, 1)
if(num[i] != cmp.num[i]) return num[i] < cmp.num[i];
return false;
}
bool operator > (const BigInt &cmp) const { return cmp < *this; }
bool operator <= (const BigInt &cmp) const { return !(cmp < *this); }
bool operator != (const BigInt &cmp) const { return cmp < *this || *this < cmp; }
bool operator == (const BigInt &cmp) const { return !(cmp < *this || *this < cmp); }
BigInt operator + (const BigInt &A) const {
BigInt S;
S.len = max(len, A.len);
FOR(i, 1, S.len){
S.num[i] += num[i] + A.num[i];
if(S.num[i] >= 10){
S.num[i] -= 10;
S.num[i + 1]++;
}
}
while(S.num[S.len + 1]) S.len++;
return S;
}
BigInt operator - (const BigInt &A) const {
BigInt S;
S.len = max(len, A.len);
FOR(i, 1, S.len){
S.num[i] += num[i] - A.num[i];
if(S.num[i] < 0){
S.num[i] += 10;
S.num[i + 1]--;
}
}
while(!S.num[S.len] && S.len > 1) S.len--;
return S;
}
BigInt operator * (const BigInt &A) const {
BigInt S;
if((A.len == 1 && A.num[1] == 0) || (len == 1 && num[1] == 0)) return S;
S.len = A.len + len - 1;
FOR(i, 1, len)
FOR(j, 1, A.len){
S.num[i + j - 1] += num[i] * A.num[j];
S.num[i + j] += S.num[i + j - 1] / 10;
S.num[i + j - 1] %= 10;
}
while(S.num[S.len + 1]) S.len++;
return S;
}
};
int main()
{
return 0;
}
函数解法
思路大体与上述一样,只不过这次用string来写一些函数而已。
(PS:开头的NR是指位数的上限)
函数形式的代码。
# include <cstdio>
# include <iostream>
# include <cstring>
# include <algorithm>
# include <cmath>
using namespace std;
# define FOR(i, a, b) for(int i = a; i <= b; i++)
# define _FOR(i, a, b) for(int i = a; i >= b; i--)
const int NR = 1000;
bool STRcompare(string str1, string str2){
int len1 = str1.size(), len2 = str2.size();
if(len1 != len2) return len1 < len2;
FOR(i, 0, len1 - 1)
if(str1[i] != str2[i]) return str1[i] < str2[i];
return false;
}
string STRaddition(string str1, string str2){
int sum[NR + 10], a[NR + 10], b[NR + 10];
memset(sum, 0, sizeof(sum));
memset(a, 0, sizeof(a));
memset(b, 0, sizeof(b));
int len1 = str1.size(), len2 = str2.size();
FOR(i, 1, len1) a[i] = str1[len1 - i] - '0';
FOR(i, 1, len2) b[i] = str2[len2 - i] - '0';
int lenS = max(len1, len2);
FOR(i, 1, lenS){
sum[i] += a[i] + b[i];
if(sum[i] >= 10){
sum[i] -= 10;
sum[i + 1]++;
}
}
while(sum[lenS + 1]) lenS++;
string ans;
_FOR(i, lenS, 1) ans += sum[i] + '0';
return ans;
}
string STRsubtraction(string str1, string str2){
int sum[NR + 10], a[NR + 10], b[NR + 10];
memset(sum, 0, sizeof(sum));
memset(a, 0, sizeof(a));
memset(b, 0, sizeof(b));
if(STRcompare(str1, str2)) swap(str1, str2);
int len1 = str1.size(), len2 = str2.size();
FOR(i, 1, len1) a[i] = str1[len1 - i] - '0';
FOR(i, 1, len2) b[i] = str2[len2 - i] - '0';
int lenS = max(len1, len2);
FOR(i, 1, lenS){
sum[i] += a[i] - b[i];
if(sum[i] < 0){
sum[i] += 10;
sum[i + 1]--;
}
}
while(sum[lenS] == 0 && lenS > 1) lenS--;
string ans;
_FOR(i, lenS, 1) ans += sum[i] + '0';
return ans;
}
string STRmultiplication(string str1, string str2){
if(str1.size() == 1 && str1[0] == '0') return str1;
if(str2.size() == 1 && str2[0] == '0') return str2;
int sum[NR + 10], a[NR + 10], b[NR + 10];
memset(sum, 0, sizeof(sum));
memset(a, 0, sizeof(a));
memset(b, 0, sizeof(b));
int len1 = str1.size(), len2 = str2.size();
FOR(i, 1, len1) a[i] = str1[len1 - i] - '0';
FOR(i, 1, len2) b[i] = str2[len2 - i] - '0';
int lenS = len1 + len2 - 1;
FOR(i, 1, len1)
FOR(j, 1, len2){
sum[i + j - 1] += a[i] * b[j];
sum[i + j] += sum[i + j - 1] / 10;
sum[i + j - 1] %= 10;
}
while(sum[lenS + 1]) lenS++;
string ans;
_FOR(i, lenS, 1) ans += sum[i] + '0';
return ans;
}
string char_to_string(char c){
string str;
str += c;
return str;
}
string int_to_string(int x){
int a[NR + 10], len = 0;
while(x != 0){
a[++len] = x % 10;
x /= 10;
}
string str;
_FOR(i, len, 1) str += a[i] + '0';
if(len == 0) str = "0";
return str;
}
int main()
{
return 0;
}
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








