C++图的深度优先遍历算法

图的结构

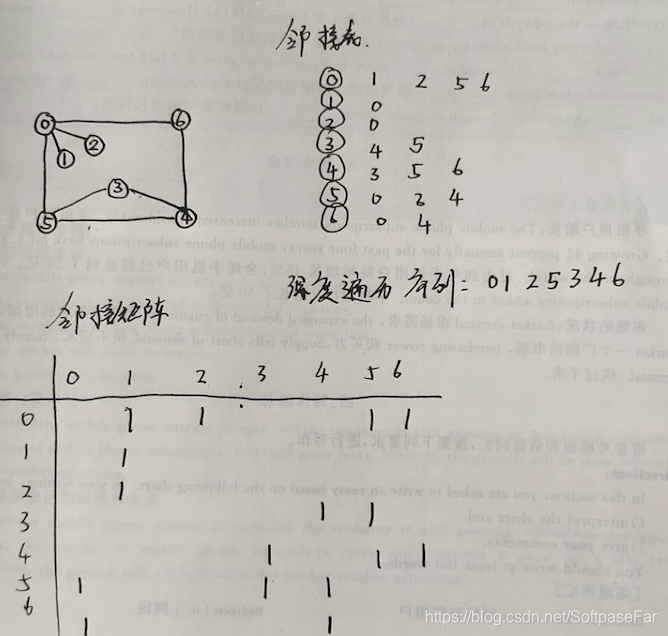
算法实现

#include <iostream>

using namespace std;
//定义顶点和边类型
typedef int VertexType;
typedef int EdgeType;
//定义顶点数和边数
#define vNums 7
#define eNums 7
//顶点是否被访问
bool visited[vNums];

//邻接矩阵定义
struct MGraph {
    VertexType vex[vNums];
    EdgeType edge[vNums][vNums];
    int vexnum, edgenum;

    MGraph(const VertexType *vs, const EdgeType (*es)[vNums]) : vexnum(vNums), edgenum(eNums) {
        for (int i = 0; i < vNums; i++) {
            vex[i] = vs[i];
        }
        for (int j = 0; j < vNums; j++) {
            for (int k = 0; k < vNums; k++) {
                edge[j][k] = es[j][k];
            }
        }
    }
};

//寻找和v相连的第一个未访问节点
int FirstNeighbor(MGraph G, int v) {
    for (int i = 0; i < vNums; i++) {
        if (G.edge[v][i] == 1 && !visited[i]) {
            return i;
        }
    }
    return -1;
}


//寻找和v相连除w的下一个未访问相连节点
int NextNeighbor(MGraph G, int v, int w) {
    for (int i = 0; i < vNums; i++) {
        if (G.edge[v][i] == 1 && !visited[i] && i != w) {
            return i;
        }
    }
    return -1;
}

//深度遍历核心算法
void DFS(MGraph G, int v) {
    cout << G.vex[v] << " ";
    visited[v] = true;
    for (int w = FirstNeighbor(G, v); w >= 0; w = NextNeighbor(G, v, w)) {
        if (!visited[w]) {
            DFS(G, w);
        }
    }


}

//深度遍历整体布局
void DFSTrave(MGraph G) {
    int v;
    for (v = 0; v < G.vexnum; v++) {
        visited[v] = false;
    }

    for (v = 0; v < G.vexnum; v++) {
        if (!visited[v]) {
            DFS(G, v);
        }
    }
}


int main() {
    //构造图（邻接矩阵）
    VertexType vex[vNums] = {0, 1, 2, 3, 4, 5, 6};
    EdgeType edge[vNums][vNums] = {
            {0, 1, 1, 0, 0, 1, 1},
            {1, 0, 0, 0, 0, 0, 0},
            {1, 0, 0, 0, 0, 0, 0},
            {0, 0, 0, 0, 1, 1, 0},
            {0, 0, 0, 1, 0, 1, 1},
            {1, 0, 0, 1, 1, 0, 0},
            {1, 0, 0, 0, 1, 0, 0}
    };
    //初始化图
    MGraph G(vex, edge);
    DFSTrave(G);
    return 0;
}

结果显示