线性代数-方世昌第三版（下）学习笔记

历代星辰监护人

已于 2023-03-19 21:24:21 修改

阅读量252

点赞数 1

分类专栏：离散数学考研复习进行时文章标签：学习

于 2023-03-06 11:44:16 首次发布

本文链接：https://blog.csdn.net/Soleil_G/article/details/129291556

版权

离散数学考研复习进行时专栏收录该内容

1 篇文章 0 订阅

订阅专栏

文章介绍了代数的基本概念，包括代数结构的构成（集合、运算、常数），详细阐述了么元、零元的定义及唯一性，以及逆元的概念。此外，还讨论了子代数的定义和封闭性，以及同态和同构在代数系统中的作用。

摘要由CSDN通过智能技术生成

根据老师上课的节奏进行总结，也算是对自己学习的复习啦！如果有错误或者疑问的地方，欢迎大家指出哇！

持续更新中……

第六章代数

代数，也叫代数结构，或者代数系统——指定义有若干运算的集合。
不关注组成代数系统的具体集合是什么，也不关注集合上的运算如何定义，而只是假设这些运算遵循某组规则，例如结合律、交换律、分配律等，根据这样的抽象代数系统，来讨论和研究该系统应有的性质，使所得结论具有普遍性。
（人话）：一个框架（某组规则），其他东西都可以往里面套，然后只研究这个框架具有什么性质。

6.1 代数结构

6.1.1代数的构成和分类方法

代数（三部分组成）：

（1）载体：一个集合。载体是我们将处理的数学目标的集合, 诸如整数、实数或符号串集合等。一般是非空集合。

（2）定义在载体上的运算：定义在载体S上的运算是从 $$$S^m$ 到S的一个映射，自然数m的值叫做运算的元数。一定要封闭

定义：设A为集合，

函数 f : A $\times$ A $\rightarrow$ A 称为A上的二元运算

函数 f : $$$A^n\rightarrow A$ 称为A上的 n元运算

n=0, 0元运算， f : $\rightarrow$ A

n=1, 一元运算，f : A $\rightarrow$ A

A 在运算 f 下是封闭的：

任何A中元素都可参与 f 运算

运算结果属于A

常见集合运算元数

集合
二元运算一元运算 0元运算

I, Q, R
$+,\times$ $-$ 0,1
$$$M_n(R)$ $+,\times$ $-$ $\theta ,E$
$\rho (B)$ $\cup ,\cap ,-,\oplus$ ~ $\O,B$
R(B) $\circ$ $$$I_B$
$$$A^A$ $\circ$

算符记号： $\circ ,*,\bullet ,\square ,\lozenge ,\triangle$ 等。
表达式：
∘ (x1, x2, …, xn) = y

       x1∘ x2 = y

△x = y

表示方法：

（1）解析表达式：

∘是实数集 R上的二元运算

x∘y = x+y-2xy

（2）一元、二元运算表（适用于有穷集）：

运算律

（1）设 ∘ , * 为A上的二元运算

交换律    $$$ {\forall}a,b\in A$ ,        a∘b=b∘a

结合律    $$$\forall a,b,c\in A$ ,     (a∘b)∘c=a∘(b∘c)

幂等律 $$$\forall a \in A$ ,          a∘a=a

分配律    $$$\forall a,b,c \in A$ ,

a∘(b*c)=(a∘b)*(a∘c),   (b*c)∘a=(b∘a)*(c∘a)

吸收律   设∘,*可交换   $$$ {\forall}a,b\in A$ ,

a∘(a*b)=a，a*(a∘b)=a

集合

运算

交换律

结合律

幂等律

I, Q, R

普通加法+

有

有

无

普通乘法 $\times$

有

有

无

Mn(R)

矩阵加法+

有

有

无

矩阵乘法 $\times$

无

有

无

ρ(B)

并 $\cup$

有

有

有

交 $\cup$

有

有

有

相对补-

无

无

无

对称差 $\oplus$

有

有

无

AA

函数复合∘

无

有

无

集合

运算

分配律

吸收律

I, Q, R

普通加法+与乘法 $\times$

$\times$ 对+可分配

+对 $\times$ 不分配

无

Mn(R)

矩阵加法+与乘法 $\times$

$\times$ 对+可分配

+对 $\times$ 不分配

无

ρ(B)

并 $\cup$ 与交 $\cap$

$\cup$ 对 $\cap$ 可分配

$\cap$ 对 $\cup$ 可分配

有

交 $\cap$ 与对称差 $\oplus$

$\cap$ 对 $\oplus$ 可分配

      $\oplus$ 对 $\cap$ 不分配

无

（3）代数常数：载体的特异元素。（可有可无）

有些代数不含常数。这里所谓“不含”只是说我们研究该代数时并不关注这些特异元素, 不一定是真的没有。

<载体，运算，常数>  可有多个

例如：

幂集合ρ(S)、并、交、补、 $\o$ 和S可构成一个代数。

  ①载体是S的幂集合ρ(S)。

②定义在载体上的运算是: 二个二元运算∪和∩、一个一元运算—（减号不封闭）。

  ③常数是 $\o$ 和S。

这个代数可记为〈ρ(S), ∪, ∩, — , $\o$ , S〉

代数通常用载体、运算和常数组成的n重组表示。

常见集合运算元数
集合	二元运算	一元运算	0元运算
I, Q, R	$+,\times$	$-$	0,1
$$$M_n(R)$	$+,\times$	$-$	$\theta ,E$
$\rho (B)$	$\cup ,\cap ,-,\oplus$	~	$\O,B$
R(B)	$\circ$		$$$I_B$
$$$A^A$	$\circ$

通常我们不去研究单个具体的代数, 而是一个种类一个种类地去研究。为此, 我们首先要知道什么样的两个代数是同一种类的。

（1）要有相同的构成成分。 如果两个代数包含同样个数的运算和常数, 且对应运算的元数相同, 则称两个代数有相同的构成成分。

例：

(1) 代数〈N , $\bullet$ ,1〉和〈I, — , 0〉有同样的构成成分, 因为都有一个二元运算和一个常数。

(2) 代数〈｛0, 1｝, ∨, ∧, 0, 1〉和〈ρ(S), ∪, ∩, $\o$ , S〉有相同的构成成分。

两个代数有相同的构成成分, 还不一定有本质的联系。

（2）要有一组相同的称为公理的规则。这里每一公理是用载体元素和代数运算的符号写成的方程。

具有相同构成成分和服从相同公理集合的代数称为同种类的。对同一种类的代数, 根据它的公理推出的一切定理, 对该种类的一切代数都成立。

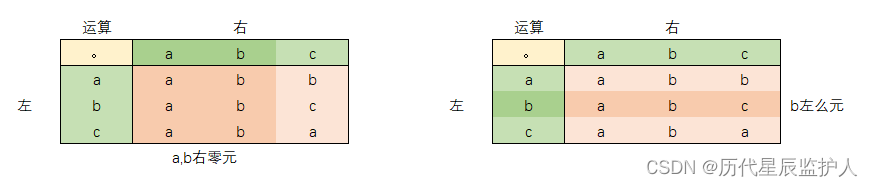
6.1.2 么元和零元

（1）定义：设 $*$ 是S上的二元运算, $$$1_l$ 是S的元素 , 如果对S中的每一元素x , 有

$$$ 1_l *x=x$

则称 $$$1_l$ 对运算 $*$ 是左么元。S中的元素 $$$0_l$ , 如果对S中的每一元素x, 有

$$$0_l *x=0_l$

则称 $$$0_l$ 对运算是左零元。

类似地可定义出右么元 $$$1_r$ 和右零元 $$$0_r$ 。

（2）定义：设 $*$ 是S上的二元运算, 1是S的元素, 如果对S中的每一元素x, 有

$1*x=x*1=x$

则称1对运算 $*$ 是么元。 S中的元素0, 如果对S中的每一元素x, 有

$0*x=x*0=0$

则称0对运算 $*$ 是零元。

左=右就是完整的元。

么元：相当于 1×其他=其他

零元：相当于 0×其他=0

（3）定理6.1-1：设*是S上的一个二元运算，具有左么元1,和右么元1,，那么1,=1,，这元素就是么元。
证：因为 $\large $$1_r$ 和 $\large $$1_l$ 是右么元和左么元。 $\large $$1_r=1_l \cdot 1_r=1_l$ 证毕。

定理6.1-2：设*是S上的二元运算，具有左零元0,和右零元0,，那么0,=0,，这元素就是零元。
证：因为 $\large $$1_r$ 和 $\large $$1_l$ 是右零元和左零元。 $\large $$1_r=1_l \cdot 1_r=1_l$ 证毕。

推论6.1-2：一个二元运算的么元（零元）是唯一的。

6.1.3 逆元

定义6.1-3：设 * 是S上的二元运算，1是对运算 * 的么元。如果x * y=1，那么关于运算 * ，x是y的左逆元，y是x的右逆元。如果x * y=1和y * x=1两者都成立，那么关于运算 * ，x是y的逆元(y也是x的逆元)。x 的逆元通常记为 $\large $$x^{-1}$ 。

存在逆元(左逆元、右逆元)的元素称为可逆的(左可逆的、右可逆的)。

定义6.1-4：设*是S上的二元运算，a∈S，如果对于每一x,y∈S，有
(a*x=a*y)V(x*a=y*a)→(x=y)
则称a是可约的或可消去的。

定理6.1-4：设 $\circ$ 是S上的可结合运算，如果元素a∈S是可逆的，则 a 也是可约的。

但是可约未必可逆。

6.2 子代数

定义6.2-1：设 $\circ$ 和 $\triangle$ 是集合S上的二元和一元运算，S'是S的子集。如果 $a,b\in S'$ ;
蕴含着 $a\circ b\in S'$ ，那么S' 对 $\circ$ 是封闭的。如果 $a\in S'$ 蕴含着 $\triangle a\in S'$ ，那么S'对 $\triangle$ 是封
闭的。

定义6.2-2：设 A=〈S， $\circ$ ， $\triangle$ ，k〉是一代数，如果
(1) $S'\subseteq S$
(2) S'对S上的运算 $\circ$ 和 $\triangle$ 封闭
(3) $k \in S'$
那么 A'=〈S'， $\circ$ ， $\triangle$ ，k〉是A的子代数。

注：（1）如果A'是A的子代数，那么A'和A有相同的构成成分和服从相同的公理。

（2）A的最大可能的子代数是它自己，这个子代数是常存在的。

（3）如果A的常数集合在A的运算下是封闭的，那么它组成A的最小子代数。这两种子代数称为A的平凡子代数，其余子代数称为真子代数。

6.3 同态

1、两个代数在结构上是一致的的要求——同构

(1)两个代数必须有相同的构成成分;
(2)两个代数的载体必须有相同的基数;
(3)两个代数的运算和常数必须遵循相同的规则。

定义6.3-1 代数A=〈 $S,*,\triangle ,k$ 〉和A'=〈 $S',*',\triangle ',k'$ 〉是同构的，如果存在一双射函数 h，使
(1) h:S→S'
(2) h(a $*$ b) =h(a) $*'$ h(b)
(3) h( $\triangle$ a) = $\triangle '$ h(a)
(4) h(k) = k'

这里a、b是S的任意元素。映射h叫做从A到A'的同构，A'叫做A在映射h下的同构象。

上述定义被推广到具有任意构成成分的代数后就是:如果双射函数h是从代数A到A'的同构，那么

(1)A和A'必须有相同的构成成分;
(2)在函数h的作用下，A的每一运算保持;
(3)函数映射A的每一常数到A'的对应常数(若A不含常数时，不须考虑这一条)。

如果A和A'是同构的代数，它们基本上是不同名的相同结构;简单地调换符号就能从 A 得到代数A'。

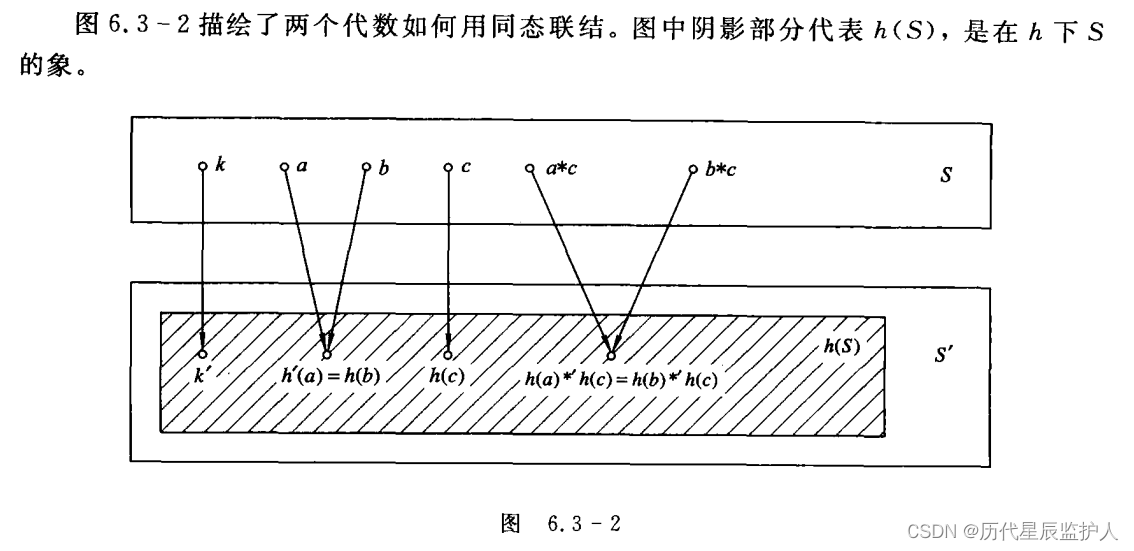
2、同态

定义6.3-2：设A=〈S，*，△，k>和A'=〈S’， $*'$ ，△'，k'>是具有相同构成成分的 $*'$ , 代数，h是一个函数。如果
(1) h:S→S
(2) h(a $*$ b) = h(a) $*'$ h(b)
(3) h( $\triangle$ a) = $\triangle '$ h(a)
(4) h ( k ) = k
这里 a、b 是S的任意元素，则称 h 是从A到A'的同态，〈h(S) , $*'$ ， $\triangle '$ ，k'>称为A在映射下的同态象。

设h是从A到A'的同态，如果h是单射的，那么称h是单一同态；如果h是满射的，那么称h是满同态；只有h 是满同态时，才称A和A'同态；如果h是双射的，即是定义6.3一1的同构。如果A=A'，那么称h是自同态；如果A=A'且h是同构，那么称h是自同构。

历代星辰监护人

关注

1
点赞
踩
1

收藏

觉得还不错? 一键收藏
0
评论
线性代数-方世昌第三版（下）学习笔记

离散数学下的笔记，持续更新中——
复制链接

扫一扫

专栏目录

集合	运算	交换律	结合律	幂等律
I, Q, R	普通加法+	有	有	无
I, Q, R	普通乘法 $\times$	有	有	无
Mn(R)	矩阵加法+	有	有	无
Mn(R)	矩阵乘法 $\times$	无	有	无
ρ(B)	并 $\cup$	有	有	有
	交 $\cup$	有	有	有
	相对补-	无	无	无
	对称差 $\oplus$	有	有	无
AA	函数复合∘	无	有	无

集合	运算	分配律	吸收律
I, Q, R	普通加法+与乘法 $\times$	$\times$ 对+可分配 +对 $\times$ 不分配	无
Mn(R)	矩阵加法+与乘法 $\times$	$\times$ 对+可分配 +对 $\times$ 不分配	无
ρ(B)	并 $\cup$ 与交 $\cap$	$\cup$ 对 $\cap$ 可分配 $\cap$ 对 $\cup$ 可分配	有
ρ(B)	交 $\cap$ 与对称差 $\oplus$	$\cap$ 对 $\oplus$ 可分配 $\oplus$ 对 $\cap$ 不分配	无

线性代数-方世昌第三版（下）学习笔记

第六章 代数

6.1 代数结构

6.1.1代数的构成和分类方法

6.1.2 么元和零元

6.1.3 逆元

6.2 子代数

6.3 同态

“相关推荐”对你有帮助么？

第六章代数