part.10 从盘古开天开始学C++之进制（下）

前言

上一节中，我们其实更多的是通过对比十进制理解进制这个事情。并通过数数、计算等方式完成了基础内容的学习。
而本节，我们需要去学习进制的转换，而这一部分则是很多比赛、考试喜欢出题的点。
因为我们需要用到幂运算，索性在前言里面给大家快速的讲解一下幂运算
同学们一定学习过乘法吧，那么乘法的本质是什么运算呢？其实乘法的本质是加法，例如4x3=>4+4+4
而幂运算的本质是乘法，例如4³=>4x4x4，指数是3就是指有3个底数4相乘就可以得到结果了！
那么有一个特例，那就是4⁰，0个4相乘结果是多少呢？记住啦，除了0以外，任何数字的0次方都是1！

以二进制转十进制为例

我们从最简单的开始理解，在日常生活中，我们通常将一个数字当成一个整体来理解和认知。但是实际上一个十进制数字每一位上的数字都有着自己的单位，从一个抽象的角度来看，他们只不过是一堆数字组合。
例如： 5297 它其实是5000、200、90、7这样四个数字组成的，其实不难发现这四个数字都是由位上数字乘以单位得到的，最终加到一起就组成了这样的数字。

单位	对应数字	计算方式
个位	1	100
十位	10	101
百位	100	102
千位	1000	103
…	…	…

通过观察，我们发现十进制数字的单位从右往左依次是10的0次方、1次方、2次方…那么大胆推断一下，其实所有进制都是这样的一个原理，对应单位也是进制的0次方依次递增。那么这个时候，我们不妨代入一个二进制的数字来计算验证一下。
例如： 101101
从右往左每一位的单位分别是2的0次方、1次方、2次方…

原数	1	0	1	1	0	1
单位	32	16	8	4	2	1
乘积	32	0	8	4	0	1

我们将乘积一栏全部加在一起32+0+8+4+0+1得到了45，接下来我们使用windows自带的计算器来验证一下。

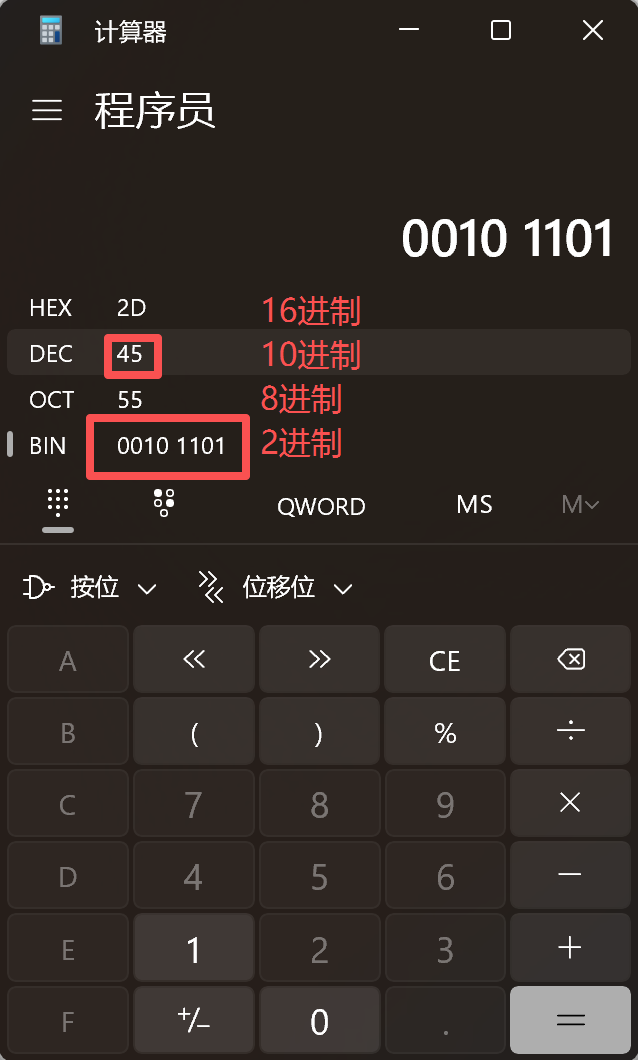
很明显，我们的计算结果并没有错，那么也由此总结出来了各个进制转十进制的通用方法。

---

我们将每一位上的数字乘以对应的单位，最终加到一起就得到了十进制的数字。单位也是从右往左，依次是进制的0次方、1次方等等以此类推

---

接下来就是大家喜闻乐见的练习环节啦，不要害怕练习没有辛勤的练习怎么才能牢固的掌握呢！
请将0b10110、0b1001、0O76、0O11、0xf1、0xa01转化成十进制噢！

通常在数字前我们加上数字0和字母b表示该数字为二进制数字，加上数字0和字母O表示该数字为八进制数字，数字0和字母x表示该数字为十六进制！
另外，我们也来认识这几个单词，对应上面的计算器中你就会恍然大悟了
binary：二进制
octal：八进制
decimal：十进制
hex：十六进制

结果是：22、9、62、9、241、2561
其实真的并没有多难对吧！

十进制转二进制

这个问题呢，我会提供两种方法，大家可以根据实际情况来选择就可以啦。
首先呢就是短除法【除2取余法】，就是把这个数字不断的除以2，将余数挨次记录下，最终余数倒着排序即得到了转化好的二进制数字。

例如，我们要把18转化成二进制
18 ÷ 2 = 9 余 0
9 ÷ 2 = 4 余 1
4 ÷ 2 = 2 余 0
2 ÷ 2 = 1 余 0
1 ÷ 2 = 0 余 1
所以18转成2进制的结果是：10010，接下来我们通过系统的计算机来验证！

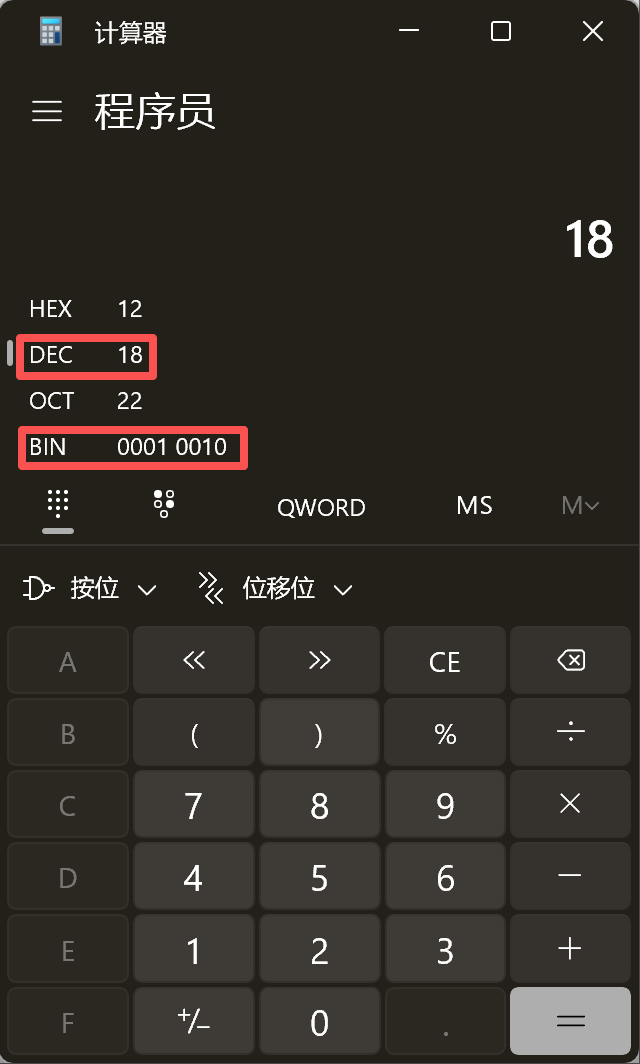
我们发现二进制数字居然是0001 0010，与我们计算出来的10010，好像不太一样。但是回想一下，我们十进制的数字，在数字的左侧加上0其实也不会有影响，比如0965和965是一致的。

验证完成，刚才我们是使用算式来演示了转化的过程，接下来我们看，在草稿纸上我们一般是如何书写的。
我们一般将商写在下方，将余数写在左侧，直到商为1时结束。从最后一个商反向将所有余数串起来就得到了最终转化的二进制的数字。

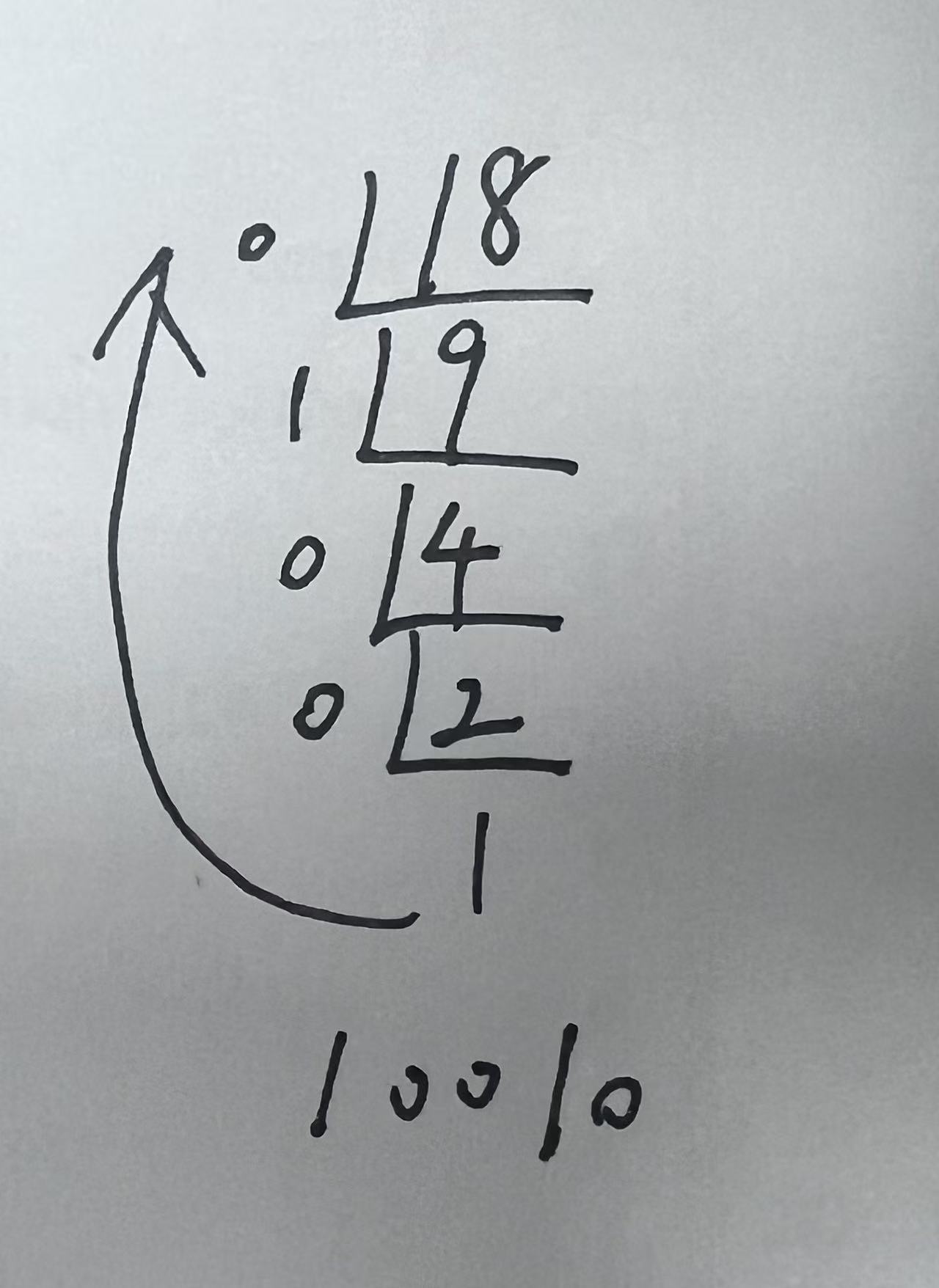
就此，第一种方法已经介绍完了，那么又来到了实践环节，你不会做不出来吧？
请将十进制数21、42、57、3转化成二进制

答案公布：10101、101010、111001、11，其实并不难吧，那么问题来了八进制，十六进制该如何转呢？相信聪明的你一定已经想到了，在短除法的基础上，我们只需要将除以2改成除以对应的进制就ok了。

第二种方法其实是一种取巧的方法。如果我问你，100和110和111这三个二进制数分别是多少呢，很简单：4，4+2，4+2+1
其实这是因为二进制的数字比较特殊，它的位上要么是1，要么是0。所以二进制数字有一个1，即需要加上其对应的单位。
例如：101001，其实就是32 + 8 + 1
那么如果此时，我们需要将74转成二进制数，我们就想从右往左二进制数的单位依次是1，2，4，8，16，32，64
到64就够了，因为下一个单位是128就已经大于64了，接下来我们只需要从大到小拼出数字74即可
64 + 0 + 0 + 8 + 0 + 2 + 0，转化成二进制就把对应位置上写上1。

单位	64	32	16	8	4	2	1
二进制	1	0	0	1	0	1	0

这种方式熟练之后就很快很快啦，例如17我们就快速得出16+1，那么二进制就是10001，快速凑出结果了。大家试试将之前的转化也用这种方式转化试试呗。

二进制与八进制、十六进制互相转化

进制转化中，二进制与八进制、十六进制的互相转化是有一定的规律和方法可以帮助我们快速的转化。①三位二进制转成一位八进制，反之亦然
②四位二进制转成一位十六进制，反之亦然
例如101 100转化成八进制，我们将101转成5，100转成4，那么这个二进制转成八进制就是54
例如0010 1111转化成十六进制，我们将0010转成2，1111转成15，那么这个二进制转成十六进制就是2f
其实这个过程非常的简单，如果数位不够那么就在左侧补零就可以了，比如1011转成八进制，那么就可以写作001 011，这样就可以分成两位八进制快速转化了
这种转化只需要我们记住就好了，本质还是非常简单的！

总结

进制的内容其实到这里就差不多了，并不算非常深入，但是正常的使用和理解已经可以啦。进制的转化没有特别复杂的内容，我们能够记住对应的计算方式，就能够完成进制的转化了，大家可以多练练。