没看懂。。。 先转了,留着以后看看……
转于:http://blog.csdn.net/yjf3151731373/article/details/51423812
#include <iostream>
#include <cstdio>
#include <cstring>
#include <string>
#include <sstream>
using namespace std;
#define N 100000
int p[N];
char str[N];
int main()
{
gets(str);
int len=strlen(str);
for(int i=len;i>=0;i--)
{
str[i+i+2]=str[i];
str[i+i+1]='#';
}
str[0]='*';
int id=0, maxt=0;
for(int i=2;i<2*len+1;i++)
{
if(id+p[id]>i)
{
p[id]=min(p[id+id-i],p[id]+id-i);
}
else
{
p[i]=1;
}
while(str[i-p[i]]==str[i+p[i]])
{
p[i]++;
}
if(i+p[i]>id+p[id])
{
id=i;
}
if(p[i]>=maxt)
{
maxt=p[i];
}
}
cout<<maxt-1<<endl;
return 0;
}
下面借鉴了大神的思维方式用DP的最优解解决,方法真的很巧妙
manacher算法:
定义数组p[i]表示以i为中心的(包含i这个字符)回文串半径长
将字符串s从前扫到后for(int i=0;i<strlen(s);++i)来计算p[i],则最大的p[i]就是最长回文串长度,则问题是如何去求p[i]?
由于s是从前扫到后的,所以需要计算p[i]时一定已经计算好了p[1]....p[i-1]
假设现在扫描到了i+k这个位置,现在需要计算p[i+k]
定义maxlen是i+k位置前所有回文串中能延伸到的最右端的位置,即maxlen=p[i]+i;//p[i]+i表示最大的
分两种情况:
1.i+k这个位置不在前面的任何回文串中,即i+k>maxlen,则初始化p[i+k]=1;//本身是回文串
然后p[i+k]左右延伸,即while(s[i+k+p[i+k]] == s[i+k-p[i+k]])++p[i+k]
2.i+k这个位置被前面以位置i为中心的回文串包含,即maxlen>i+k
这样的话p[i+k]就不是从1开始
由于回文串的性质,可知i+k这个位置关于i与i-k对称,
所以p[i+k]分为以下3种情况得出
//黑色是i的回文串范围,蓝色是i-k的回文串范围,
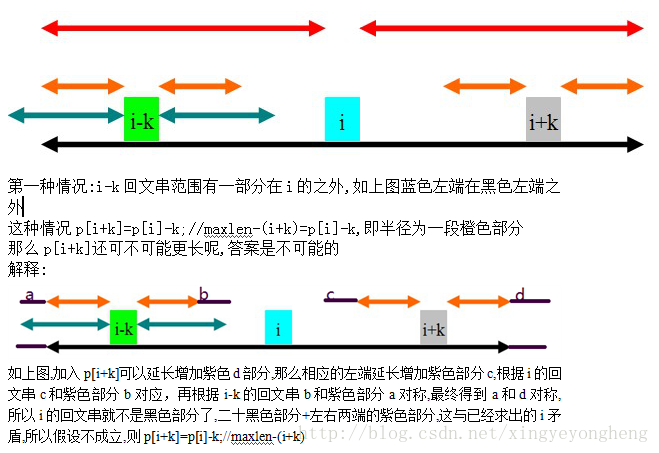








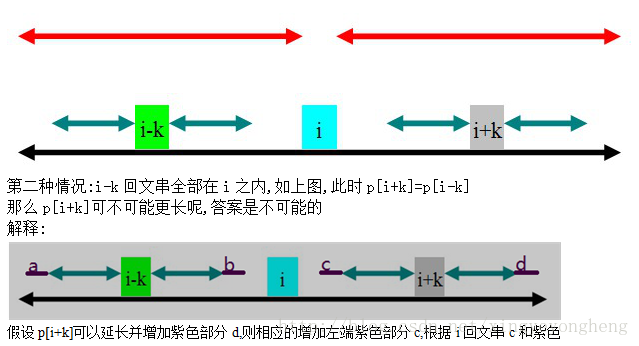
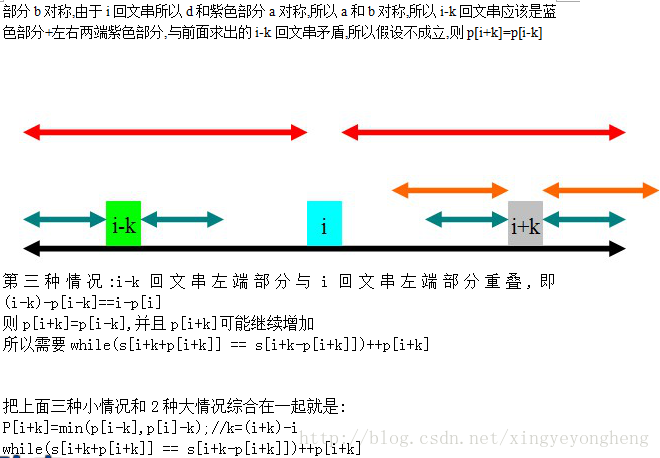














 471
471

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








