今天做笔试题时,遇到一道构造哈希表的题,hash函数是 k%11 ,然后一个数组记不清了,然后就是问二次探测法进行,问下面那个是正确,懵逼啊,没做过,不知道,乱选直接下一题,于是有这个博客,赶紧学习一波。
网上查询了一下。
构造哈希表的几种方法
常用方法是直接定址法和除留余数法
- 直接定址法(取关键字的某个线性函数为哈希地址)
类似于这样的式子
f(key) = a × key + b
- 除留余数法(取关键值被某个不大于散列表长m的数p除后的所得的余数为散列地址)
对于散列表长为m的散列函数公式为:
f( key ) = key mod p ( p ≤ m )
mod是取模(求余数)的意思。事实上,这方法不仅可以对关键字直接取模,也可在折叠、平方取中后再取模。
-
平方取中法
-
折叠法
-
随机数法
-
数学分析法
哈希冲突(碰撞)以及处理
哈希冲突:既然有哈希函数Hash(key),在有限的空间里,肯定会产生相同的的值(哈希地址),我们称这种情况为哈希冲突(碰撞)。任意的散列函数都不能避免产生冲突。
1. 开发定址法
所谓的开放定址法就是一旦发生了冲突,就去寻找下一个空的散列地址,只要散列表足够大,空的散列地址总能找到,并将记录存入。
- 线性探测法
fi(key) = (f(key)+di) MOD m (di=1,2,3,......,m-1)
用开放定址法解决冲突的做法是:当冲突发生时,使用某种探测技术在散列表中形成一个探测序列。沿此序列逐个单元地查找,直到找到给定的关键字,或者碰到一个开放的地址(即该地址单元为空)为止(若要插入,在探查到开放的地址,则可将待插入的新结点存人该地址单元)。查找时探测到开放的地址则表明表中无待查的关键字,即查找失败。
ep:我们的关键字集合为{12,67,56,16,25,37,22,29,15,47,48,34},表长为12。 我们用散列函数f(key) = key mod 12。
当计算前S个数{12,67,56,16,25}时,都是没有冲突的散列地址,直接存入:
计算key = 37时,发现f(37) = 1,此时就与25所在的位置冲突。
于是我们应用上面的公式f(37) = (f(37)+1) mod 12 = 2。于是将37存入为2的下标位置。
接下来22,29,15,47都没有冲突,正常的存入:
到了 key=48,我们计算得到f(48) = 0,与12所在的0位置冲突了,不要紧,我们f(48) = (f(48)+1) mod 12 = 1,此时又与25所在的位置冲突。于是f(48) = (f(48)+2) mod 12=2,还是冲突……一直到 f(48) = (f(48)+6) mod 12 = 6时,存入该位置:
我们把这种解决冲突的开放定址法称为线性探测法。
- 二次探测法
考虑深一步,如果发生这样的情况,当最后一个key=34,f(key)=10,与22所在的位置冲突,可是22后面没有空位置了,反而它的前面有一个空位置,尽管可以 不断地求余数后得到结果,但效率很差。
因此我们可以改进di = 12, -12, 22, -22,……, q2, -q2 (q <= m/2),这样就等于是可以双向寻找到可能的空位置。
对于34来说,我 们取di即可找到空位置了。另外增加平方运算的目的是为了不让关键字都聚集在 某一块区域。我们称这种方法为二次探测法。
f(key) = (f(key)+di) MOD m (di = 1^2, -1^2, 2^2, -2^2,……, q^2, -q^2, q <= m/2)
注:1^2 表示是 1的平方。
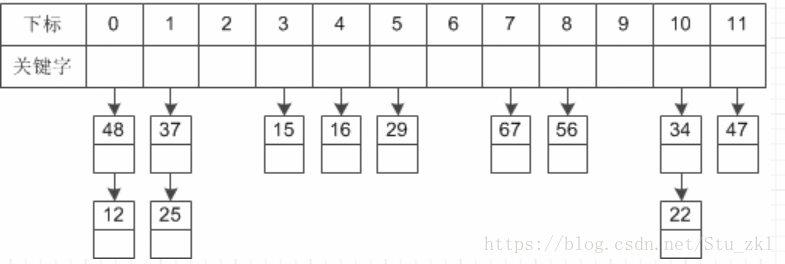
2. 链地址法
前面我们谈到了散列冲突处理的开放定址法,它的思路就是一旦发生了冲突,就去寻找下一个空的散列地址。那么,有冲突就非要换地方呢,我们直接就在原地处理行不行呢?
答案是可以的,就是链地址法,就好比Java里的HashMap的数据结构一样。
关于HashMap源码分析 ——> https://blog.csdn.net/Stu_zkl/article/details/82714325
好了,就写到这了。


























 1092
1092











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








