【算法】算法设计与分析课程笔记第三章动态规划_算法设计与分析动态规划第一行两个整数n和c,物品个数和背包容量;随后n行表示每个-CSDN博客

本文链接：https://blog.csdn.net/Summerison/article/details/133651502

1.1 动态规划简介

1.1.1 引例

动态规划算法和分治法类似，基本思想也是将待求解问题分解成若干个子问题，子问题可以以继续拆分，直到问题规模达到临界条件即可。多说无益，举个例子来解释一下：

这其实是一个多阶段图求最短路的问题，路径大体上是 A→B→C→D→E，但是每到一个节点时就需要面临许多选择，所有选择中加起来最短的那一组就是要求的答案。

我们可以用动态规划的思想来分析这个问题，最开始从A出发，我们要选择一条最短的路，那么就可以把这个大问题先分成两个：从A到B和从B到E，这样就把大问题拆成两个小问题了，接下来，从A到B有两个选择，分别是B1和B2，它们和从B到E的路径相连，接下来就可以继续拆分，从B1到E和从B2到E又可以拆分成两个小问题，那就是从B到C和从C到E.......就这样一直拆下去，直到最后从D到E，这样再往回返回最短路径，直到得到整个问题的最短路径。

1.1.2 算法总体思想

从上面我们知道，动态规划算法也是不断地拆分问题，但是这里和之前的递归又有所不同，因为动态规划类的问题中，分解得到的子问题一般不会是相互独立的，也就是说有可能得到相同的子问题，所以在计算中，如果单单应用了递归，有些子问题就会被重复计算。

因此，适合使用动态规划来解决的问题一般都有下面两个性质：

1. 最优子结构性质

一个问题的最优解包含了其子问题的最优解。

2. 重叠子问题性质

在问题的求解过程中，很多子问题的解会被多次使用。

3.1 矩阵连乘问题

PTA 算法第三章习题1

7-1 矩阵连乘

题目

矩阵的乘法定义如下：设A是m×p的矩阵，B是p×n的矩阵，则A与B的乘积为m×n的矩阵，记作C=AB，其中，矩阵C中的第i行第j列元素cij就是A的第i行元素和B的第j列元素一一相乘后累加。

当多个矩阵相乘时，采用不同的计算顺序所需的乘法次数不相同。例如，A是50×10的矩阵，B是10×20的矩阵，C是20×5的矩阵，则计算ABC有两种方式：(AB)C和A(BC)；

前一种需要 50×10×20+50×20×5=15000 次计算，后一种则只需 10×20×5+50×10×5=3500 次。

设A1,A2,...,An为矩阵序列，Ai是阶为Pi−1∗Pi的矩阵(1≤i≤n)。试确定矩阵的乘法顺序，使得计算A1A2...An过程中元素相乘的总次数最少。

输入格式:

每个输入文件为一个测试用例，每个测试用例的第一行给出一个正整数n(1≤n≤100)，表示一共有n个矩阵A1,A2,...,An，第二行给出n+1个整数P0,P1...Pn，以空格分隔，其中1≤Pi≤100(0≤i≤n)，第i个矩阵Ai是阶为Pi−1∗Pi的矩阵。

输出格式:

获得上述矩阵的乘积，所需的最少乘法次数。

输入样例:

在这里给出一组输入。例如：

5
30 35 15 5 10 20

输出样例:

在这里给出相应的输出。例如：

非递归解法

要求矩阵连乘的最小值，不使用递归解法的话，就只能一个一个去尝试，也就是遍历，我们的遍历是用三层for循环来实现的；

首先我们设置两个数组，其中的一维数组用来存放输入的矩阵行列数，由于可以相乘的两个矩阵中，前一个矩阵的列数等于后一个矩阵的行数，所以不需要重复存放，设数组为p[ ] ，则 p [ i - 1 ] 存放的是第 i 个矩阵的行数， p [ i ] 存放的就是第 i 个矩阵的列数；

另外一个数组是二维数组 dp [ ] [ ] ，设置下标为 i 、j ，那么dp [ i ] [ j ] 就代表从第 i 个矩阵乘到第 j 个矩阵的值，在遍历完成后，每个位置存放的都会是连乘的最小值；

有了两个辅助数组还不够，我们要解决连乘问题，最关键的是得到题解的方法，我们用的是动态规划算法，动态规划算法的核心是递推表达式，如下：

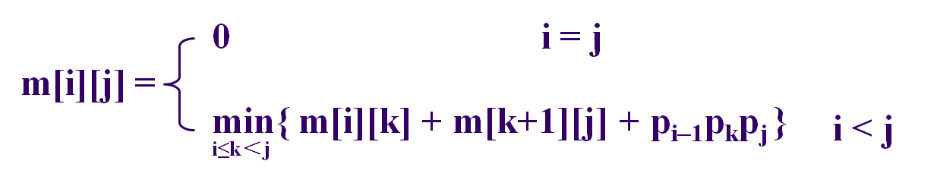
上式中的m数组就是dp数组，当两个下标相等时，就说明只有一个矩阵在连乘，这是没有乘积的，所以将其值设置为0；

如果i和j不相等，说明是从第i个矩阵乘到第j个，此时可以设置一个k，代表连乘中分隔矩阵的括号，令k遍历从i到j的所有值，可以得到多个不同的连乘结果，取其中最小的放入dp数组中；

这里的遍历虽然只在一段矩阵中设置了一个括号分隔处，但是由于用括号分隔的子矩阵段已经设置好了最小连乘值，所以这样做是可以的，这其实也是分治的思想；

因此，我们还必须保证较小的矩阵段已经设置好了最小值，所以在填表时，也就是设置dp矩阵元素值时，需要从i最大、j最小的地方开始设置，这其实通过递推公式也可以看出。

下面是具体的代码实现：

#include<bits/stdc++.h>
using namespace std;

int n; // 矩阵数 
int p[1000]; //  p[i]存储的是第i个矩阵的列数，p[i-1]存储的是第i个矩阵的行数 
int dp[1000][1000];  // 看成一个i*j的矩阵，其中的存放的是从第i个矩阵到第j个矩阵的最小连乘积 

int minimum () {
	for (int i = 1; i <= n; i++) // 但是全局数组的初值已经自动设置为0了，所以可以省略 
		dp[i][i] = 0; // 单个矩阵连乘相当于没有连乘，所以令乘积为0 
	for (int i = n; i >= 1; i--) { // 从n最大的部分开始填表，因为递推公式里求i时有用到i+1 
		for (int j = i + 1; j <= n; j++) { // 当i=n时，j=n+1，不满足条件，不循环，之后就可以了 ，而且j必然要大于等于i 
			dp[i][j] = dp[i][i] + dp[i+1][j] + p[i-1]*p[i]*p[j]; // 递推公式，设置连乘的初值为括号在第一个矩阵后 
			for (int k = i + 1; k < j; k++){
				int temp = dp[i][k] + dp[k+1][j] + p[i-1] * p[k] * p[j]; // 括号从第二个矩阵直到倒数第二个矩阵j-1遍历 
				if (temp < dp[i][j]) {
					dp[i][j] = temp;
				}
			} 		
		}							 
	} 
	return dp[1][n];
}
int main(){
	cin >> n;
	for(int i = 0; i <= n; i++){
		cin >> p[i];
	}
	int result = minimum();
	cout << result;
	return 0; 
}

递归+备忘录解法

#include<bits/stdc++.h>
using namespace std;

int n; // 矩阵数 
int p[1000]; // 矩阵的行列数 
int dp[1000][1000]; // 连乘最小值 

int setdp(int i, int j) {
	if (dp[i][j] > 0)
		return dp[i][j];
	if (i == j)
		return 0;
	dp[i][j] = setdp(i, i) + setdp(i + 1, j) + p[i - 1] * p[i] * p[j];
	for (int k = i + 1; k <j; k++) {
		int tmp = setdp(i, k) + setdp(k + 1, j) + p[i - 1] * p[k] * p[j];
		if (tmp < dp[i][j])
			dp[i][j] = tmp;
	}
	return dp[i][j];
}

int main() {
	cin >> n;
	for (int i = 0; i <= n; i++) {
		cin >> p[i];
	}
	cout << setdp(1, n);
	return 0;
}

PTA 算法第三章习题2

7-1 最长公共子序列

题目

求两个字符串的最长公共子序列长度。

输入格式:

输入长度≤100的两个字符串。

输出格式:

输出两个字符串的最长公共子序列长度。

输入样例1:

ABCBDAB
BDCABA

输出样例1:

输入样例2:

ABACDEF
PGHIK

输出样例2:

思路

用动态规划来求解，两个字符串的最长公共子序列的递推公式如下：

我们在求解时，先定义两个字符串 x 和 y，x表示第一个字符串，y表示第二个字符串；

再定义一个二维数组 c [ ] [ ] 作为备忘录，c [ i ] [ j ] 表示将 x 从第一个字符截至第 i 个字符的字符串和将 y 从第一个字符截至第 j 个字符的子串的最长公共子序列长度；

当 i = 0 或 j = 0 时，两个字符串中至少有一个为空，此时最长公共子序列为0；

当i和j都不为0时，如果 x 和 y 的最后一个字符相等，那么此时的 c [ i ] [ j ] 至少为1，再加上 x 和 y 各自去掉最后一个字符而剩下的两个字符串的最长公共子序列长度；如果 x 和 y 的最后一个字符不相等，那么取 x 或 y 分别一个去掉最后一个字符并且另一个不变的最长公共子序列的最大值作为c [ i ] [ j ] 的值。

代码

#include<bits/stdc++.h>
using namespace std;

char x[110], y[110];
int m, n, c[110][110];

int dp() {
    for (int i = 1; i <= m; i++) {
        for (int j = 1; j <= n; j++) {
            if (x[i - 1] == y[j - 1])
                c[i][j] = c[i - 1][j - 1] + 1;
            else
                c[i][j] = max(c[i - 1][j], c[i][j - 1]);
        }
    }
    return c[m][n];
}

int main() {
    cin >> x >> y;
    m = strlen(x);
    n = strlen(y);

    cout<<dp();

    return 0;
}

PTA 算法第三章习题3

7-1 01背包问题

题目

给定n(n<=10)种物品和一个背包。物品i的重量是wi，价值为vi，背包的容量为C(C<=1000)。问:应如何选择装入背包中的物品，使得装入背包中物品的总价值最大? 在选择装入背包的物品时，对每种物品i只有两个选择：装入或不装入。不能将物品i装入多次，也不能只装入部分物品i。可以不剪枝。

输入格式:

共有n+1行输入：第一行为n值和c值，表示n件物品和背包容量c；接下来的n行，每行有两个数据，分别表示第i(1≤i≤n)件物品的重量和价值。

输出格式:

输出装入背包中物品的最大总价值。

输入样例:

输出样例:

思路

把物品看成二进制的数位，放入了背包就赋值为1，不放入背包就赋值为0，最后的结果就是一串二进制数，我们可以这样来理解，但实际上不是这么做的，我们还是用动态规划来做。

首先是分解子问题，举个例子，要求5个物品放入背包的最优解，其实可以先求一下后4个物品放入背包的最优解，再算一下将第5个物品放入背包的最优解，如果不放入的值更大，那就不放，反之就放入；但如果第5个的重量已经比现在背包的容量小了，那么就直接跳过第5个，把4个物品的最优解赋值给5个物品的情况。

按这样的逻辑推下去，最后推到只剩下一个物品，这就是最后的临界情况，在递归求解中就是临界情况，在非递归的填表法中，这就是最先需要填的那一栏，因为基于上面那样的逻辑，可以得到下面的递推表达式：

非递归解法

#include<bits/stdc++.h>
using namespace std;

int n, c;
int w[1010], v[1010];
int m[1010][1010];

// m[i][j]表示从第i个物品到第n个物品存储与否的最优解，也就是最大的总价值 
// 当新加入的物品重量小于当前的背包容量时，
//  m[i][j] = max(m[i + 1][j], m[i + 1][j - w[i]] + v[i]);
// 当新加入的物品重量大于当前背包容量时，不加入该物品 
// m[i][j] = m[i + 1][j]； 
// 考虑到临界情况，也就是只有一个物品要加入背包的时候，对所有背包容量的情况进行判断，
// 当第n个物品的重量小于背包容量时，
// m[n][j] = w[n];
// 当第n个物品的重量大于背包容量时，
// m[n][j] = 0; 

int dp() {
	for (int j = 0; j <= c; j++) {
		if (j >= w[n])
			m[n][j] = v[n];
		else 
			m[n][j] = 0;
	}
	for (int i = n - 1; i >= 1; i--) {
		for (int j = 0; j <= c; j++) {
			if (j >= w[i])
				m[i][j] = max(m[i + 1][j], m[i + 1][j - w[i]] + v[i]);
			else
				m[i][j] = m[i + 1][j];
		}
	}
	return m[1][c];
}

int main() {
	cin >> n >> c;
	for (int i = 1; i <= n; i++)
		cin >> w[i] >> v[i];
	cout << dp();
	return 0;
}