【数据结构】判断一个二叉树是否是二叉搜索树(三种思路)/二叉搜索树中删除一个节点/找一个节点的中序后继节点 (含思路/c++代码)

bool IsbinaryST(Node* root)//检查root这棵树是不是二叉搜索树
{
    if(root==NULL)return 1;
    else{//检查根节点的左/右子树中有没有比根节点大/小的数  同时检查其左右子树是否符合二叉搜索树的条件
        if(IsSubtreelesser(root->left,root->data) 
        && IsSubtreeGreater(root->right,root->data)
        && IsbinaryST(root->left) && IsbinaryST(root->right))
        return 1;
    }
    return 0;
}

下面是两个检查数据大小的函数

bool IsSubtreeGreater(Node* root,int data)//检查root节点及以下有没有比data大的数
{
    if(root==NULL)return 1;
    else{
        if(root->data>=data && IsSubtreeGreater(root->left,data)
        && IsSubtreeGreater(root->right,data))
            return 1;
    }
    return 0;
}
bool IsSubtreelesser(Node* root,int data)//检查root节点及以下有没有比data小的数
{
    if(root==NULL)return 1;
    else{
        if(root->data<=data && IsSubtreelesser(root->left,data)
        && IsSubtreelesser(root->right,data))
            return 1;
    }
    return 0;
}

这种方法主要就是对递归思想的理解，就不再多写啦。

只是这种思路好想但是由于递归函数比较多可能代码效率比较低，并且我们在第一遍遍历左右子树将每个节点值与根节点比较之后，还会不断的重复遍历第一次遍历过的节点(特别是比较靠下的节点会被遍历比较很多次)并比较大小，这样使得函数执行成本很高。

更新每个节点的数据范围

第二种思路就是我们知道随着树不断向下拓展，每个节点符合二叉搜索树的数据的范围就会确定下来，我们通过不断更新节点应该具有的数据范围，来避免多次遍历节点比较大小，实现是否是二叉搜索树的判断。像下面这样

所以这里相较第一种思路的区别就是lesser greater这两个函数。

bool IsBstUtil(Node* root,int minV,int maxV)
{
    if(root==NULL)return 1;
    else{
        if(root->data>minV && root->data<maxV
        && IsBstUtil(root->left,minV,root->data)
        && IsBstUtil(root->right,root->data,maxV))
            return 1;
    }
    return 0;
}
bool IsbinarySearchTree(Node* root)
{
    return IsBstUtil(root,INT_MIN,INT_MAX);//传递数据上下限
}

对于根节点的输入数据，我们将其范围划定在[INT_MIN,INT_MAX]上，代表最小-最大正整数这个范围。

判断中序遍历结果是否是有序数列

我们知道中序遍历的原则是：左根右。按照二叉搜索树的特点，刚好中序遍历出来应该是一个有序数列。

中序遍历我们之前已经写过他的函数，这里我们主要思考如何在中序遍历的同时判断其是否有序？

我想到的判断有序的方式是创建一个vector<int>型的数组，将读取过的数据(也就是在遍历函数中依次打印的数据)存入数组中，在数组不为空的情况下，将即将打印的数据大小与数组中最后一位数据大小进行比较。一旦不符合大小关系判断结果就出来了。

只是函数中的递归函数在有根节点的同时还要将这个数组也进行传递，这样保证传入的是同一个数组才能进行比较。这里使用了&操作符，避免了不断递归重复创建数组占用空间。

bool Inorder(Node* root,vector<int> &A)
{
    if(root==NULL)return 1;
    if(!Inorder(root->left,A))return 0;//确定左子树为二叉搜索树
    if(!A.empty() && root->data<=A.back())return 0;//确定其是否有序
    A.push_back(root->data);
    return Inorder(root->right,A);//确定右子树是否是二叉搜索树
}

这种当然是不够简洁的代码，更好的方法是我们只需要记录下前一个数据的大小即可

Node* previous=NULL;
bool IInorder(Node* root)
{
    if(root==NULL)return 1;
    if(!IInorder(root->left))return 0;
    if(previous!=NULL && previous->data>root->data)return 0;
    previous=root;
    return IInorder(root->right);
}

这种思路我还是没有直接想起来，好像与指针相关的我貌似不太敢用这种心理，自然也经常想不到了。。对指针还要再敏感一点。

二叉搜索树中删除一个节点

删除节点的部分思路应该还是挺好想的。我们知道树是通过链表进行链接的，有了之前链表的经验，我们应该很容易想到关于删除二叉搜索树中的一个节点，主要工作就是对其指向的链接的更改。其次就是记得释放删除节点的空间。注意我们删除了某个节点之后仍然要保证其作为二叉搜索树所具有的性质

那么对于二叉搜索树来说有的节点有0/1/2个孩子，我们想到对叶子节点和单个节点的删除应该是比较容易的。对于这两种情况来说更改链接并不会影响其二叉搜索树的性质

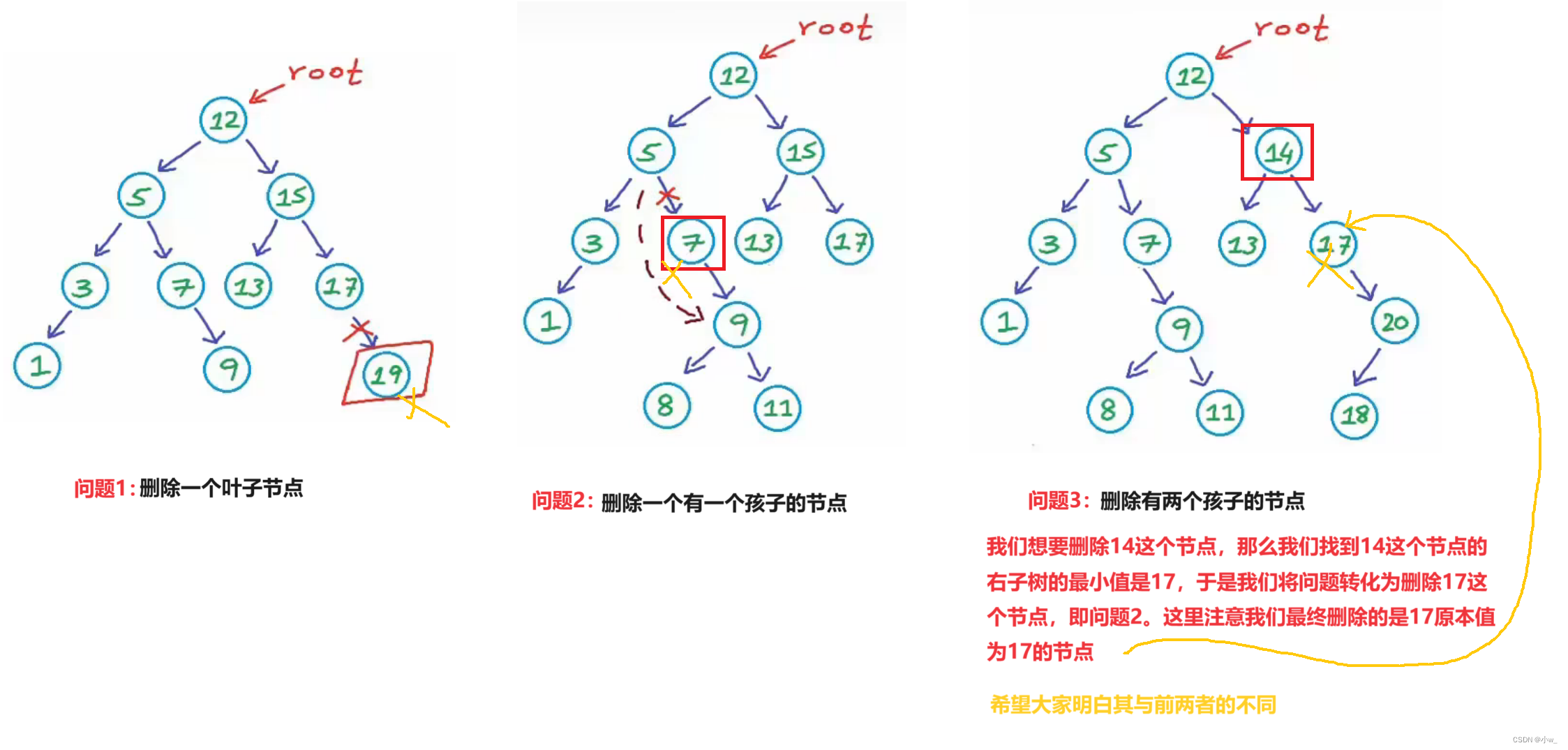
删除叶子节点：只需要修改其父节点的孩子(也就是该节点)指向为NULL即可，随后释放空间。

删除有一个孩子的节点：将其父节点的对应孩子指向更改为其孩子节点即可。

当要删除一个有两个孩子的节点时，相比就要复杂一点了。因为有两个孩子，所以我们不知道如何将其父节点更改指向，指向其中一个孩子另一个孩子就会丢失，同时我们还要考虑到在删除该节点之后其仍然是二叉搜索树。

于是，在删除有两个孩子的节点时，我们想到将要删除的数据更改为该节点右子树的最小值(或者是左子树的最大值，这里以前者举例)，因为右子树的最小值一定是大于左子树上所有节点的值同时小于右子树上其他数据的值，且由于我们取的是最小值，所以代表着这个节点没有左孩子，我们就将问题转化为了删除一个0/1个孩子节点的问题。

代码如下

#include<iostream>
using namespace std;
struct Node{
    int data;
    Node* left;
    Node* right;
};
Node* Getnode(int data)
{
    Node* temp=new Node();
    temp->data=data;
    temp->left=temp->right=NULL;
    return temp;
}
void Insert(Node* &root,int data)
{
    if(root==NULL)root=Getnode(data);
    else{
        data>root->data?Insert(root->right,data):Insert(root->left,data);
    }
}
Node* Findmin(Node* root)
{
    if(root==NULL)return root;
    else{
        if(root->left==NULL)return root;
        else{
            return Findmin(root->left);
        }
    }
}
Node* Delete(Node* &root,int data)
{
    if(root==NULL)return root;
    else{
        if(data>root->data)root->right=Delete(root->right,data);
        else if(data<root->data)root->left=Delete(root->left,data);
        else{//当要删除的数据=此时的root->data
            if(root->left==NULL && root->right==NULL){//0个孩子
                delete root;
                root=NULL;
            }
            else if(root->left==NULL){//1个
                Node* temp=root;
                root=root->right;
                delete temp;
            }
            else if(root->right==NULL){//1个
                Node* temp=root;
                root=root->left;
                delete temp;
            }
            else{//2个
                Node* temp=Findmin(root->right);//找到右子树的最小值
                root->data=temp->data;
                root->right=Delete(root->right,temp->data);
            }
        }
    }
    return root;
}
void Inorder(Node *root)
{
    if (root == NULL)
        return;
    Inorder(root->left);
    printf("%d ", root->data);
    Inorder(root->right);
}
int main()
{
    Node* root=NULL;
    Insert(root,20);
    Insert(root,200);
    Insert(root,12);
    Insert(root,2);
    Insert(root,7);
    Insert(root,22);
    Insert(root,30);
    Insert(root,5);
    Insert(root,500);
    root=Delete(root,5);
    root=Delete(root,12);
    root=Delete(root,200);
    Inorder(root);
    return 0;
}

一些解释

这里想对删除有一个孩子的节点的代码进行解释

else if(root->left == NULL) {
    struct Node *temp = root;
    root = root->right;
    delete temp;
    return root;
}

这里我们定义了一个指向root的temp指针，注意这里并不是耗费空间新创建了一个节点，只是一个指向root空间的指针；后面我们将root更新为root->right，可以理解为我们将root父节点的右指针指向了root->right，然后使用temp指针来保存并最终释放了被删除元素root的空间。(这里刚开始有点困惑没反应过来hh)

找一个节点的中序后继节点

中序后继节点就是通过中序遍历，该节点后面的那个节点。

我们如果采用执行中序遍历，来得到当前节点的中序后继节点的话，时间复杂度应该为O(n)，成本比较高。而作为二叉搜索树在数据的插入删除查找其时间复杂度为O(h)，那么我们希望这个操作最终时间复杂度也达到O(h)

对于BST的中序遍历（即左-根-右的顺序），我们会得到一个升序的序列。这就意味着，对于BST中的任何一个节点，它的中序后继节点就是比它大的最小节点

于是我们思考另一种思路，我们发现，如果我们要找的节点有右子树，那么该节点的中序后继节点也就是其右子树的最小值，这个想一下可以理解哈；如果该节点没有右子树，那么，如下图

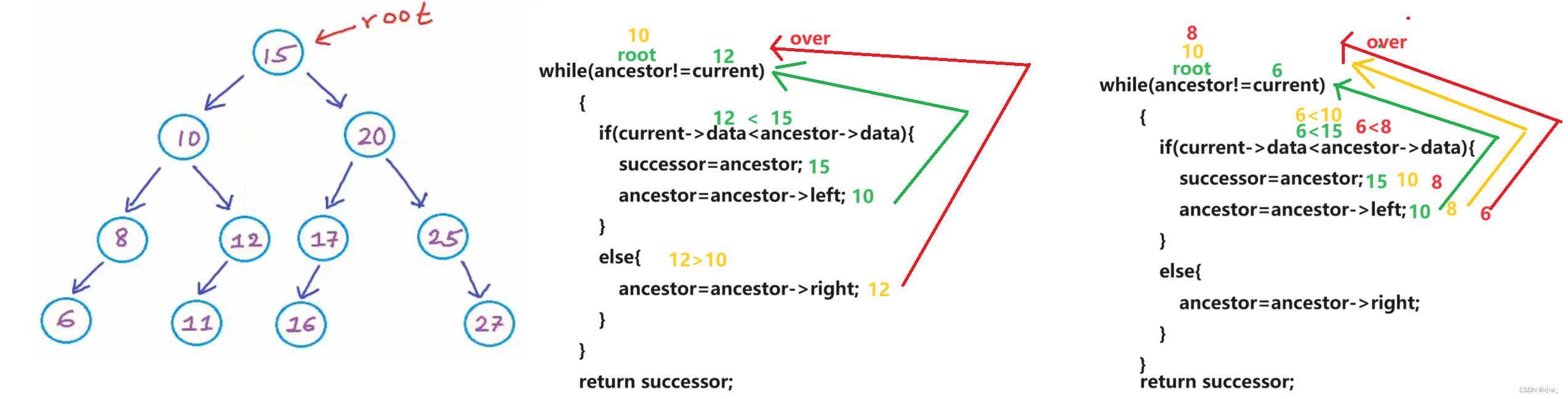
我们将没有右子树的情况又进行细分：如果该节点在其父节点的左边，容易想到其中序后继节点应该就是其父节点，因为中序遍历左根右嘛；如果该节点在其父节点的右边，那么我们就要找比它大的最小的祖先节点：从root开始逐渐向下找，如果当前节点的值小于或等于目标节点的值，那么我们就向右走；否则，我们就向左走，并更新中序后继节点

代码如下

#include<iostream>
using namespace std;
struct Node{
    int data;
    Node* left;
    Node* right;
};
Node* Getnode(int data)
{
    Node* temp=new Node();
    temp->data=data;
    temp->left=temp->right=NULL;
    return temp;
}
void Insert(Node* &root,int data)
{
    if(root==NULL)root=Getnode(data);
    else{
        data>root->data?Insert(root->right,data):Insert(root->left,data);
    }
}
//找到该节点的位置
Node* Find(Node* root,int data)
{
    if(root==NULL)return NULL;
    else if(root->data==data)return root;
    else if(data<root->data)return Find(root->left,data);
    else return Find(root->right,data);
}
//找最小值
Node* Findmin(Node* root)
{
    if(root==NULL)return NULL;
    while(root->left!=NULL)root=root->left;
    return root;
}
Node* Getsuccessor(Node* root,int data)
{
    Node* current=Find(root,data);
    if(current==NULL)return NULL;
    if(current->right!=NULL){//该节点有右子树，那么其中序后继节点就是其右子树中最左的节点
        return Findmin(current->right);
    }
    else{//该节点没有右子树
        Node* successor=NULL;
        Node* ancestor=root;
        while(ancestor!=current)
        {
            if(current->data<ancestor->data){//说明该节点是其父节点的左孩子
                successor=ancestor;//暂时赋值为中序后继节点
                ancestor=ancestor->left;//不断更新以找到比它大的最小的祖先节点
            }
            else{//该节点为其父节点的右孩子
                ancestor=ancestor->right;//我们要向右找
            }
        }
        return successor;
    }
}
int main()
{
    Node* root=NULL;
    Insert(root,20);
    Insert(root,200);
    Insert(root,12);
    Insert(root,2);
    Insert(root,7);
    Insert(root,22);
    Insert(root,30);
    Insert(root,5);
    Insert(root,500);
    Node* successor=Getsuccessor(root,2);
    if(successor==NULL)cout<<"No successor Found\n";
    else cout<<successor->data;
    return 0;
}