[笔记]牛顿方法·指数族·GLMs

牛顿方法(Newton’s method)

牛顿方法是另一种最大化$l(\theta )$的算法。
首先找到一个实数域上的方程$f$，$f(\theta )=0$，θ是实数。

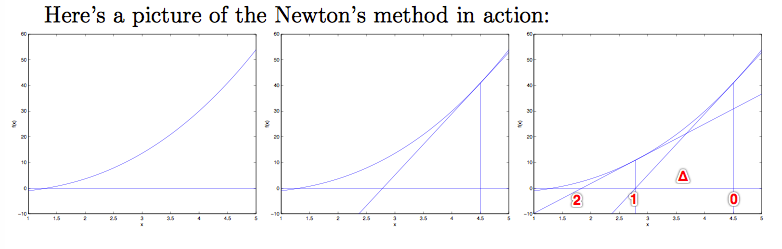
从起始点${\theta }_0$开始，找到$f({\theta }_0)$处的切线，与坐标轴相交于${\theta }_1$，由此不断迭代。两点之间的距离记为Δ 。
$f’(θ_0)=\frac{f(θ_0)}{Δ} $ ----> $Δ=\frac{f(θ_0)}{f’(θ_0)} $
所以牛顿方法执行更新规则：$$\theta :=\theta -\frac{f(\theta )}{f^{\prime }(\theta )}$$
如果想要找到θ使得$l(\theta )$最大，那么θ就该满足$l^{\prime }(\theta )=0$，由此可见我们可以将牛顿方法运用其中，$f(\theta )=l^{\prime }(\theta )$。
$$\theta :=\theta -\frac{l^{\prime }(\theta )}{l^{\prime \prime }(\theta )}$$
在一般化的牛顿方法中，θ通常一个向量，所以一般化的牛顿方法(也称作Newton-Raphson method) 为：
$$\theta :=\theta -H^{-1}{▽}_{\theta }l(\theta )$$
其中，${▽}_{\theta }l(\theta )$表示$l(\theta )$对${\theta }_i^{\prime }s$的偏导数；
H表示黑塞矩阵(Hessian matrix)，是二阶导数矩阵。
$$H_{ij}=\frac{{\partial }^{2}l(\theta )}{\partial {\theta }_i\partial {\theta }_j}$$
由此可见，该式也是一阶导数除以二阶导数。
总得来说，牛顿方法比梯度上升算法减少了迭代次数，但是其缺点是每次迭代都要重新计算H矩阵的逆，如果在大规模数据中涉及很多特征，那么这将花费巨大代价。

---

指数分布族(Exponential family distributions)

指数族：
$$p(y;\eta )=b(y)exp({\eta }^{T}T(y)-a(\eta ))$$
其中，
η被称作自然参数或正则参数(natural parameter/canonical parameter);
$T(y)$被称作充分统计量(sufficient statistic)，通常$T(y)=y$；
$a(y)$是log partition function，$e^{-a(\eta )}$是一个规范化常数，使得分布$p(y;\eta )$的和为1。
对于给定的一组a,b,T，都会得到对应的指数分布族，而且改变参数η的取值会影响该指数族的分布。

伯努利分布(Bernoulli)的指数分布族

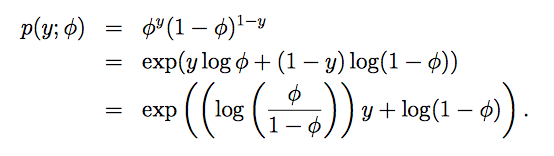
本例中η为标量，所以$\eta =log(\phi /(1-\phi ))$，即$\phi =1/(1+e^{-\eta })$。
这样我们就得到了一个logistic函数，也说明了伯努利分布的参数φ与自然参数η存在特定的关系。
指数分布族：

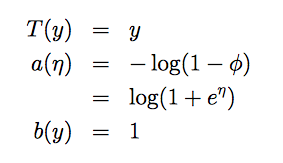
高斯分布(Gaussian)的指数分布族

在学习线性回归时，发现高斯分布的方差对最终结果并没有任何影响。所以为了简化问题，令${\sigma }^2=1$。

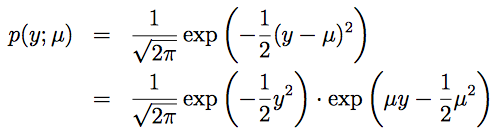
指数分布族：

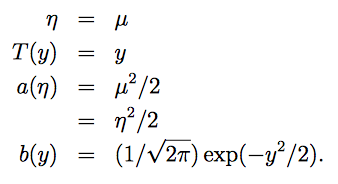
以下分布也都可以写成指数分布族的形式：
多项式分布(multinomial)
泊松分布(poisson)：用于计数的建模。
伽马分布(gamma)，指数分布(exponential):用于对正数建模，多用于间隔问题。
β分布，Dirichlet分布：用于对小数建模。

---

GLMs

广义线性模型(Generalized Linear Models)
构造GLMs来解决问题，我们首先需要了解三个设计假设。

1. $y|x;\theta \sim ExponentialFamily(\eta )$。
2. 我们的目标是通过给定x，来预测T(y)期望($E[T(y)|x]$)。由于通常T(y)=y，因此假设函数需要满足$h(x)=E[y|x]$(这个假设对logistic回归和线性回归都成立)。
3. 自然函数η与输入特征x的关系是线性的，$\eta ={\theta }^{T}x$(如果自然参数是向量，${\eta }_i={\theta }_i^{T}x$)。

如果我们的问题需要满足这三个假设，那么我们就可以通过构造广义线性模型来解决。

最小二乘法

在线性回归的最小平方问题中，目标变量y(在GLM的术语中也称作响应变量(response variable))是连续的，给定x，y的条件分布符合高斯分布，均值为μ。套用前面GLM的推导，我们有μ=η。所以，我们可以得到线性回归的假设函数就是：

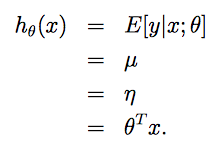
Logistic回归

在二元分类问题中，给定x，y服从伯努利分布，均值为ϕ。同样利用前面的推导，可以得到logistic回归的假设函数就是：

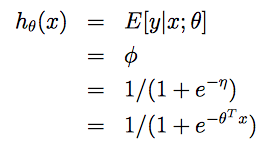
再介绍一些有关知识：
正则响应函数(canonical response function)：$g(\eta )=E[T(y);\eta ]$
正则关联函数(canonical link function)：$g^{-1}$

Softmax回归

多项式分布，多类别分类问题。
假设 y ∈ { 1 , 2 , . . . , k } y \in \{1,2,...,k\} y∈{1,2,...,k}，可以用一个k维的向量来表示分类结果，当y=i时，向量的第i个元素为1，其它均为0。这样表示是存在冗余的，因为如果我们知道了前k-1个元素，那么第k个其实就已经确定了，因此我们可以只用k-1维向量来表示。
设置参数：${\phi }_1,{\phi }_2,...,{\phi }_{k-1}$，${\phi }_i=p(y=i;\phi )$。
由此可见：${\phi }_k=1-{\sum }_{i=1}^{k-1}{\phi }_i$。

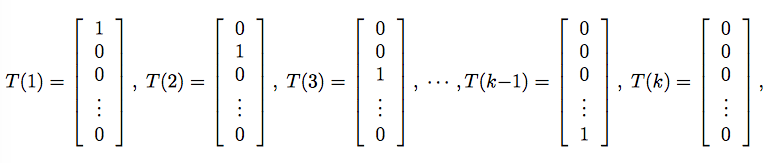
注意，这里就和前面的T(y)=y不同了，这里的T(y)是一个向量，所以用$T(y{)}_i$表示T(y)的第i个元素。在往后的推导过程中，会出现***1{True}=1，1{False}=0***的判别函数。所以T(y)与y的关系可以写成：
T ( y ) i = 1 { y = i } T(y)_i=1\{y=i\} T(y)i​=1{y=i}
$$E[T(y{)}_i]=P(y=i)={\phi }_i$$
多项式分布的指数分布族：

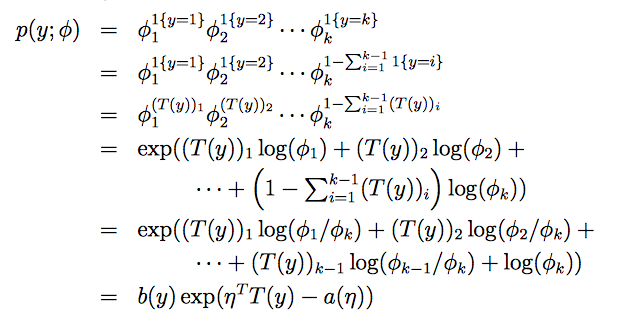
可以得到：

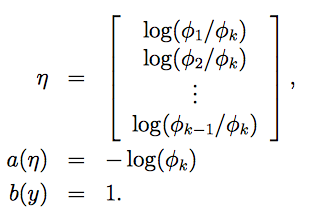
链接函数为${\eta }_i=log\frac{{\phi }_i}{{\phi }_k}$,为了简化，令${\eta }_k=0$，可得响应函数：

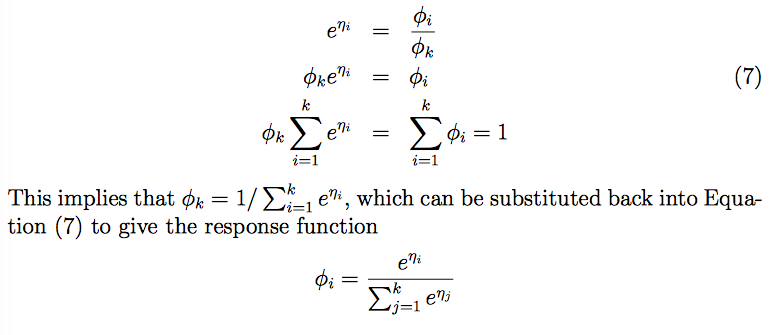
这个从η到φ’s的映射被称作softmax函数。
根据假设3，并且令${\theta }_k=0$，${\eta }_k={\theta }_k^{T}x=0$，得到softmax回归模型，它是logistic回归的推广。

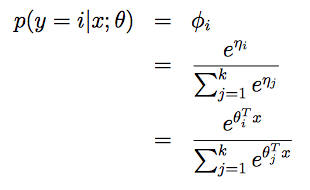
所以我们假设函数的输出为：

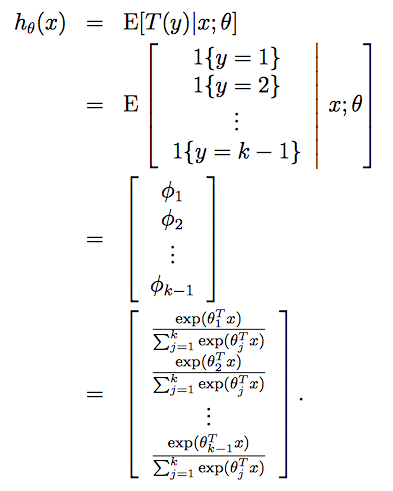
最后就是回归问题的参数的学习了，依然可以使用极大似然估计的方法来学习θ，似然函数为：

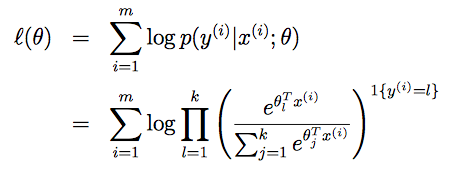
之后就可以通过梯度上升或牛顿方法来求出合适的参数θ。