分治算法在树的路径问题上的应用

                                                         分治算法在树的路径问题中的应用

【摘要】

         树作为一类特殊的数据结构，在信息学中有着极为重要的作用，各类关于树的题目在竞赛中更是屡见不鲜。本文选取了近几年出现的关于树的路径的题目，并结合例题讲解了分治算法在此类问题上的应用。

【关键字】

       树 路径 路径剖分 分治 数据结构        

【序言】

       树被定义为没有圈的连通图，具有以下几个性质：

      1. 在树中去掉一条边后所得的图是不连通的。
      2. 在树中添加一条边后所得的图一定存在圈。
      3. 树的每一对顶点U和V之间有且仅有一条路径。

      由于树具有一般图所没有的特点，因此在竞赛中有着更加广泛的应用，尤其是关于树中路径的问题，即一类以路径为询问对象的题目，更是频繁的出现在各种比赛中，每一个有志于OI及ACM的选手都应该掌握这类问题的法。     

      分治，指的是分而治之，即将一个问题分割成一些规模较小的相互独立的子问题，以便各个击破。我们常见的是在一个线性结构上进行分治，而在本文中我们将会讲解分治算法在树结构上的运用，称之为树的分治算法。 分治往往与高效联系在一起，而树的分治正是一种用来解决树的路径问题的高效算法。 下面让我们一起来感受树的分治算法的美妙吧。

【正文】
一.树的分治算法
      下面给出树的分治算法的两个常见形式：
基于点的分治：

       首先选取一个点将无根树转为有根树，再递归处理每一颗以根结点的儿子为根的子树。

基于边的分治：

       在树中选取一条边，将原树分成两棵不相交的树，递归处理。

效率分析：
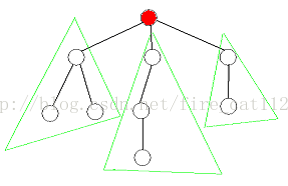
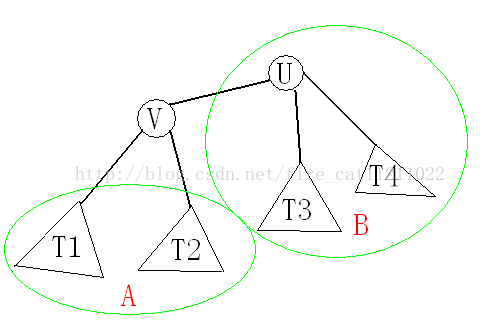
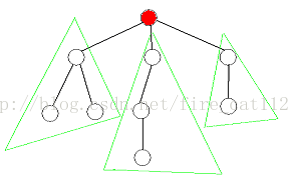
      首先我们考虑如何选取点（边）。对于基于点的分治，我们选取一个点，要求将其删去后，结点最多的树的结点个数最小，这个点被称为“树的重心”。而基于边的分治，我们选取的边要满足所分离出来的两棵子树的结点个数尽量平均，这条边称为“中心边1”。而对于这两个问题，都可以使用在树上的动态规划来解决，时间复杂度均为O(N)，其中N 为树的结点总数。
     对于树的分治算法来说，递归的深度往往决定着算法效率的高低，下面我们来分析上述两种方式的最坏递归深度。
     定理1：存在一个点使得分出的子树的结点个数均不大于N / 2
     证明：
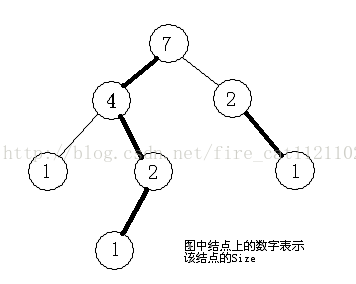
     假设U 是树的重心，它与V1,V2...Vk相邻，记Size(X)表示以X 为根的子树的结点个数。记V 为V1...Vk 中Size值最大的点。我们采取反证法，即假设Size(V) > N /2，那么我们考虑如果选取V 作为根结点的情况，记Size'(X)表示此时以X 为根的子树的结点个数。
     如下图，对于 A部分，显然Size'(Ti) < Size(V)，对于 B部分，Size' (U) = N-Size(V) < N/2<Size(V)，这与我们假设矛盾。

     定理得证。

    

     由定理1 可得，在基于点的分治中每次我们都会将树的结点个数减少一半，因此递归深度最坏是O(log N)的，在树是一条链的时候达
到上界。
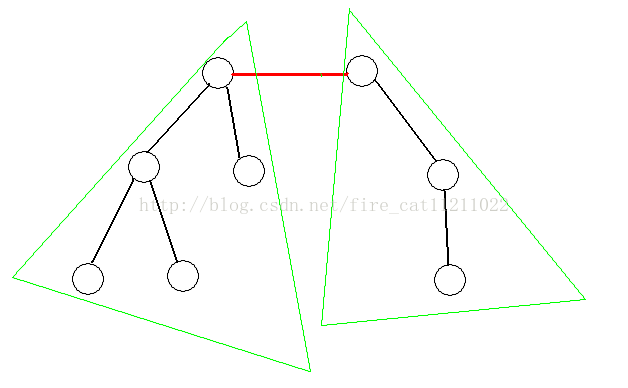
     定理2：如果一棵树中每个点的度均不大于D，那么存在一条边使得分出的两棵子树的结点个数在[N /(D+1),N*D/(D+1)]。(N >= 2)
      证明： 
      不妨令D 为所有点的度的最大值。
      当D=1时，命题显然。
      当D>1时，我们设最优方案为边U -V ，且以U,V 为根的两棵子树的结点个数分别为S和N - S，不妨设S >= N - S。
      设X 为U 的儿子中以X 为根的子树的结点个数最大的一个，我们考虑另一种方案X -U，设除去边X -U后以X 为根的子树结点个数为P。显然P >= (S -1) /(D-1)，由于P < S 且边U -V是最优方 案 ,所 以 N - P >= S , 与 P >= (S -1) /(D-1) 联 立 可 得S <= ((D-1)N +1) / D，又N >= D+1，所以S <= N *D/(D+1)。
      证毕。

      由定理2 我们可以得到在D为常数时，基于边的分治递归最坏深度为O(log N)。
      但是在一般的题目中，D可能较大甚至达到O(N)，这时这个算法的效率十分低，因此在本节中我们只考虑使用基于点的分治。

【例1】树中点对统计
       给定一棵N(1<= N<=10000)个结点的带权树，定义dist(u,v)为u,v两点间的最短路径长度，路径的长度定义为路径上所有边的权和。再给定一个K(1<=K<=1000000000) ，如果对于不同的两个结点a,b，如果满足dist(a,b) <=K，则称(a,b)为合法点对。
       求合法点对个数。
       算法分析
       如果使用普通的 DFS 遍历，时间复杂度高达O(N*N)，而使用时间复杂度为O(NK)的动态规划，更是无法在规定时限内出解的。

       我们知道一条路径要么过根结点，要么在一棵子树中，这启发了我们可以使用分治算法。

                          

       路径在子树中的情况只需递归处理即可，下面我们来分析如何处理路径过根结点的情况。

       记Depth(i)表示点i到根结点的路径长度，Belong(i) = X ( X 为根结点的某个儿子，且结点i 在以X 为根的子树内)。那么我们要统计的就是：
       满足 Depth(i) + Depth(j) <=K 且 Belong(i) != Belong( j) 的(i, j) 个数 =  满足Depth(i)  Depth( j) K的(i, j)个数 –  满足Depth(i) + Depth( j) <=K且Belong(i) = Belong( j)的(i, j)个数
       而对于这两个部分，都是要求出满足Ai+ Aj <=k的(i, j)的对数。将A排序后利用单调性我们很容易得出一个O(N)的算法，所以我们可以用O(N log N)的时间来解决这个问题。
       综上，此题使用树的分治算法时间复杂度为O(N*logN*logN)。

【例2】Free Tour 2

      给定一棵含有N 个结点的带权树，其中结点分为两类，黑点和白点。

      要求找到一条路径，使得经过的黑点数不超过K 个，且路径长度最大。
      数据范围：
                  N <= 200000
   算法分析
      由于N 最大可以达到200000 ，朴素的算法很难在给定的时限内通过数据。但考虑到此题维护的对象是树的路径，我们尝试使用树的分治来解决该题。

      与上题相同，我们只需要考虑过根结点的路径，其余的递归处理即可。

      我们记G(i, j)表示从根的第i个儿子到其子树中某点的最优路径的长度，其中要求此路径上的黑点不超过j 个。

      我们记Dep(i)表示根结点的第i个儿子到其子树内的点的路径上最多的黑点个数。

      那么我们可以得到当 j >Dep(i)时，G(i, j) =G(i,Dep(i))，所以我们只需保留 j <=Dep(i)的部分，这样就可以用DFS

在O(N)的时间内算出 G。那么我们的目标就是求出 Max{G[u,L1]+G[v, L2]} 其中u!=v,且L1+ L2 = K -siBalck [Root ]。

当x 为黑点时，Black[Root] =1,否则Black[Root]= 0。

这个问题我们很容易用平衡树来做到O(N log N)，从而总复杂度为O(N*logN*logN)。这里值得注意的是O(K + Nlog N)

的方法是不能够使用的，否则整个算法的时间复杂度将会变为O(NK +N*logN*logN) 。

      在这里我们介绍一个不需要高级数据结构的方法，可以发现

u!=v可以变为u>v.

     所以关键在于如何维护Max{G[v,L2]}(v < u)。假设我们已经得到了Max{G[v,L2]}(v <u-1)，我们考虑如何将前者与G[u -1]合并来得到Max{G[v,L2]}(v < u)。

    显然Max{G[v,L2]}(v <u) =Max{Max{G[v,L2]}(v<u),G[u -1,L2]}

注意到我们并没有显式的计算出G[u]，而只是保留它的前若干位，所以两个保留长度分别为Len1,Len2的合并运算的

时间复杂度为O(Max{Len1,Len2})。

我们记根结点的儿子个数为TotChild ，那么如果直接按上述方法做的话， 总的计算次数为：

Dep(1)+Max{Dep(1),Dep(2)} +...+Max{Dep(1)...Dep(TotChild)}，最坏将会达到O(N*N) ，幸运的是我们发现根结点的

儿子顺序对答案是不会有影响的。因此我们首先对根结点的儿子按Dep(i)为关键字排序，然后由Dep(i)从小到大的顺

序进行计算，这样我们的计算次数就变为了Dep(1)Dep(TotChild)  N，所以排序之后我们的时间复杂度为

O(N)。

      由于边的个数是O(N)的，所以在排序这个环节我们的总复杂度不超过O(N log N)，所以整个算法的时间复杂度为O(N log N)。

【本节小结】

      在这一节中我们讲述的是树的分治算法在一类路径的计算和统计问题的运用。树的分治算法之高效，我们可以从

上面的两道例题就可窥见一斑。

       在这一节中我们主要讲解的是如何使用基于点的分治解决题目，而读者可以发现在基于点的分治中，子树的个数

可能会较多，这给我们的维护带来了困难。

       而在上面两道例题中如果使用基于边的分治的话，算法的分析将会更加简单，这是因为基于边的分治则只需要维

护两棵子树，这样看来，基于边的分治在思考的复杂度上小于基于点的分治，这是基于边的分治的一大优势。

       但是正如我们上面讲的，较大的最坏时间复杂度是基于边的分治的致命伤，但这并不说明基于边的分治无用武之

地，我们将在第三节中探讨如何使基于边的分治的时间复杂度能够得到保证。

 二．树的路径剖分算法：
    【例3】Query On a Tree
      有一棵包含N 个结点的树，每条边都有一个权值，要求模拟两种操作：
      1)改变某条边的权值
      2)询问U,V 之间的路径中权值最大的边。
      数据范围:
                  N <=10000
      算法分析

      如果使用单纯的模拟，那么对于第二种操作，虽然期望复杂度是O(log N)的，但最坏复杂度将达到O(N)。在大量

的询问下，这个算法是无法在题目要求的时限内出解的，我们需要更好的算法。

  引入路径剖分

      考虑到虽然这颗树的边权在不断改变着，但树的形态并未改变，因此考虑将这棵树的路径进行剖分，这里介绍一

种在实践中常用的剖分方法：

轻重边路径剖分

      我们将树中的边分为两类：轻边和重边。

                                                                            

       记Size(U)表示以U 为根的子树的结点个数，令V 为U 的儿子中Size最大的一个，那么我们称边(U,V)为重边，其余边为轻边。

       显然轻重边路径剖分具有如下性质
       性质1：
            如果(U,V)为轻边，则Size(V)  Size(U) /2
       性质2：
            从根到某一点的路径上轻边的个数不大于O(log N)
       性质3：

           我们称某条路径为重路径，当且仅当它全部由重边组成。那么对于每个点到根的路径上都不超过 O(log N)      

       条轻边和O( lo gN)条重路径。

      现在我们回到原题，对树进行轻重边路径剖分。对于询问操作，我们可以分别处理两个点到其最近公共祖先的路

径。根据性质3，路径可以分解成最多O(log N)条轻边和O(log N)条重路径，那么只需考虑如何维护这两种对象。

      对于轻边，我们直接处理即可。而对于重路径，我们只需用线段树来维护。这个算法对于两种操作的时间复杂度

分别为O(log N) ，O(logN*logN）5次方可以在时限内通过本题的所有数据了。

【例4】黑白树
       你拥有一棵有N 个结点白色的树——所有节点都是白色的。接下来，你需要处理C 条指令：
      1.修改指令：改变一个给定结点的颜色（白变黑，黑变白）；
      2.查询指令：询问从结点1 到一个给定结点的路径上第一个黑色结点编号。
      数据范围:
          N <=1000000,C <=1000000
     算法分析
         初看此题，我们感觉不是很好下手，“到一个给定结点的路径上第一个黑色结点编号”似乎也没有什么特殊的性质，也很难找到一个数据组织方式能够直接维护，这使得我们陷入了僵局。
         由于本题中树的形态没有改变，且我们需要维护的对象是一个点到根的路径，我们考虑使用路径剖分。
         与上面一题不同的是，上题我们需要维护的是若干边的最大值，而这题我们需要的维护的对象变成了点。
         不过，我们仍然可以使用路径剖分，由路径的剖分方式可以知道每个点都属于且仅属于一条重路径，所以我们只需考虑重路径，不需要考虑轻边，这样比起上一题来说需要考虑的对象变少了。而维护重路径相当于解决线性结构上的问题，使用堆或线段树都可以达到目的。
【小结】
        路径剖分的作用是使需要维护的对象从复杂的树型结构变为我们熟悉的线性结构，从而轻松解决题目。
路径剖分与树的分治的联系：
      由于路径剖分与树的分治均可以解决树中路径的问题，我们不禁疑问，它们是否有着千丝万缕的联系呢?答案是肯定的。

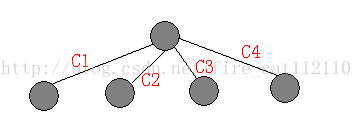
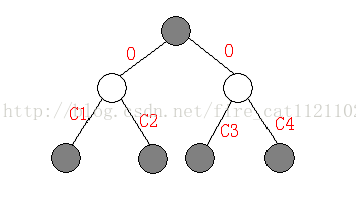
      我们首先画出一棵树及其剖分(如图(a))，我们似乎看不出有什么特殊，我们不妨把它的样子稍加改变(如图(b))，按照点到根结点路径上的轻边个数分层摆放。

       这时我们就能明显的看出路径剖分与树的分治两种算法其实有着惊人的相似，我们上一节中介绍了分治的两种方式：删除一个点，或一条边，而路径剖分相当于每次删除了一条链！所以路径剖分算法可以看做是基于链的分治，而且这种分治还有一个特点，每次被删除结点的儿子必将作为下一次删除的链的头结点。这样，就给我们的维护带来了方便。而正如我们第一节中讲的，每个点到根结点路径上的轻边个数是O(log N)的，这样算法的时间复杂度便有了保证。

【例5】Query On a Tree Ⅳ
         给定一棵包含N 个结点的树，每个节点要么是黑色，要么是白色。要求模拟两种操作：
       1)改变某个结点的颜色。
       2)询问最远的两个黑色结点之间的距离。
       数据范围：
               N <=100000
        边权的绝对值不超过1000
算法分析
       此题的出处为ZJOI2007，虽然问题是一样的，但是不同的是此题的边权可能为负。

        原题的标准做法是利用括号序列的性质，但是括号序列是不能在有负边权的树上使用的，因此我们必须另寻他法。

        注意两个结点的距离，就是路径的长度，我们试图使用路径剖分来解决此题。

         一般来说路径剖分算法都是以点到根的路径作为维护对象，这道题的算法似乎与路径剖分无关，但是只要我们想到分治算法的本质是基于链的分治后，这题便可以迎刃而解。

       下面我们考虑如何计算路径的最高点在此条链中的最优值。对于一条链，记此链的结点个数为N，D(i),D2(i)为此

链的第i个结点向下至某个黑色结点的路径中长度的最大值和次大值。(两条路径仅在头结点处相交。如果至黑色结点

的路径不存在，那么长度记为负无穷)

        我们的目标就是要求出满足与此链的重合部分在1, N的路径的 最大长度。我们可以利用线段树来维护。 对于一个区间[L,R]，我们记录
       MaxL=Max{Dist(L, i) + D(i)}
       MaxR=Max{D(i) + Dist(i,R)}
       Opt =与此链的重合部分在[L, R]的路径的最大长度
       Dist (i, j)表示链上的第i个点到第 j个点的距离。
      设区间[L,R]的结点编号为P，Lc,Rc分别表示P的左右两个儿子，区间[L,Mid]和[Mid +1, R]，我们可以得到如下转移：
           MaxL(P) =Max{MaxL(Lc),Dist(L,Mid +1) +MaxL(Rc)}

          MaxR(P) =Max{MaxR(Rc),MaxR(Lc)+Dist(Mid,R)}

                                                                                     Opt(Lc),Opt(R,c),

         Opy(P)=Max{  MaxR(Lc)+MaxL(Rc)+Dist(Mid,Mid+1)}
        由于Dist(i, j) = Dist(1, j) - Dist(1, i)，所以Dist(i, j)是可以 O(1)算出的。
        对于边界情况[L, L]，设此区间的结点编号为P，此链的第L个结点为x ，那么
                 MaxL(P) = D(L)
                 MaxR(P) = D(L)

                   点x为黑色时，Opt(P) =Max{D(L),D(L) + D2(L)}，
           否则，Opt(P) = D(L) + D2(L)
           问题就只剩下如何维护D 和D2 的值。

           我们记C1...Ck 表示x的k 个儿子(不包括同层结点)，Li 表示Ci所在的链的线段树根结点，Cost(p)表示(x, p)的边权。那么点x向下至某个黑色结点的路径的长度集合为：

              {MaxL(Li) +Cost(Ci),0} x为黑色结点
              {MaxL(Li) +Cost(Ci)} x为白色结点
            我们可以用堆来维护这个集合，这样D(x),D2(x)的获取就是O(1)的了。

            对于询问操作，我们可以用一个堆存贮每条链的最优值，这样我们就可以做到每次询问的时间复杂度为O(1)。

            对于修改操作，由于一个点只会影响O(log N)条链，每次都需要更改堆中的值和线段树，所以每次修改的时间复杂度为 (log ) 2 O N 。
           值得一提的是，如果使用在下一节所讲的改变树的结构的方法，整个程序的编程复杂度会更低。
【本节小结】

         通过对路径剖分更深一步的分析，我们发现了路径剖分算法可以理解为基于链的分治，使一道看上去与路径剖分无关的题目顺利得到解决。

三．树的分治的进一步探讨：
          如何改进基于边的分治的时间复杂度

      首先，我们试图改变选择边的标准，可惜这是改变不了算法的最坏时间复杂度的，当树的形态类似与如图所示时，无论选择哪条边，结果都是一样的。

      注意到算法的复杂度分析的决定性因素是每个点的度数，我们猜想是否可以通过等价的转换，使原图转化成一个

每个点的度数是常数级别的新图呢？

      我们再来回想例5，它所关注的对象是两个黑点之间的距离，这就提醒我们可以在不影响树中黑色结点之间的距离的前提下加入白色结点！

      经过尝试，我们可以利用如图的方式使原图得到等价的转化。

                                                       

                                                                                    

                                                          

       可以看到通过巧妙的对每个结点到其儿子的路径中加入了白色结点，使之成为了类似线段树的结构，而长度为N

的线段树共有2N个结点，所以含有N 个结点的树转化后所得的新树最多包含2N 个结点。

      而且这个转化给予了我们原树所没有的性质，那就是每个点的度至多为3！

      幸运的是，这个改变树结构的方法是可以推广的。白色结点代表的是不影响结果的中间结点，我们可以用这个方

法来解决一般的问题。

使用基于边的分治解决【例2】
      这是在第一节中出现的例题，当时我们使用基于点的分治解决了此题，时间复杂度为O(N log N)。
      使用基于边的分治与基于点的分治基本上是相同的，但与基于点的分治所不同的是，基于边的分治只需要考虑两棵子树，所以设计算法更为简单。此题使用基于边的分治，时间复杂度为O(N log N)。

使用基于边的分治解决【例5】
      基于边的分治将路径分成了两类，一类是属于某个子树，另一类是经过中心边。前者我们可以通过递归，下面只考虑如何维护后者。
      我们记点x到其根结点的距离为Dep(x)，那么目标就转化为求Max{Dep(x)+Dep(y)+MidCost}，其中x, y均为黑色结点，且属于不同的子树。MidCost 表示中心边的权值。
      我们只需要使用两个堆来维护Dep(x)，这样我们就可以用O(1)的时间得到答案。
      对于反色操作，由于每个点仅属于O(log N)棵树，所以时间复杂度为 (log ) 2 O N 。
      这样，我们就达到了与使用路径剖分同阶的时间复杂度。但算法更为简单。

四．全文总结

       我们对前几节所讲的算法作一个简单的总结。

       在算法的常数方面，树的路径剖分算法是当中常数最小的算法，基于点的分治其次，基于边的分治常数较大。

       在算法的应用范围方面，基于链的分治与基于点(边)的分治有所不同。前者的特点在于每次被删除结点的儿子必

将作为下一次删除的链的头结点，这一点是基于点(边)的分治无法达到的。所以前者可以用来维护路径上的点(边)，但

如果维护的对象是路径的长度，后者的能力更强。

       与基于点的分治比较，基于边的分治在设计高效算法的思考难度上明显小于前者。 这几个算法各有所长，需要我

们根据具体情况，灵活运用，以最佳的方式解决题目。

        只要我们做到勤于思考，善于总结，我们就一定会更上一层楼！

【参考文献】
1.《算法艺术与信息学竞赛》 刘汝佳、黄亮 2.杨哲 2007年国家集训队作业 《QTREE 解法的一些研究》 3.楼天城 2004年国家集训队作业 《树中点对距离统计解题报告》
【感谢】
感谢廖晓刚老师在我写这篇论文时对我的指导。 感谢刘鹰同学和杭州二中的孙征同学对我的论文提供的帮助。
【附录】
例1原题：http://acm.pku.edu.cn/JudgeOnline/problem?id=1741
例2原题：http://www.spoj.pl/problems/FTOUR2/
例3原题：http://www.spoj.pl/problems/QTREE/
例5原题：http://www.spoj.pl/problems/QTREE4/