Treap平衡树学习

最新推荐文章于 2023-11-07 21:52:05 发布

StaroForgin

最新推荐文章于 2023-11-07 21:52:05 发布

阅读量229

点赞数 2

分类专栏： ------数据结构------ # 平衡树 # 二叉搜索树

本文链接：https://blog.csdn.net/Tan_tan_tann/article/details/103245430

版权

------数据结构------ 同时被 3 个专栏收录

113 篇文章 1 订阅

订阅专栏

平衡树

15 篇文章 0 订阅

订阅专栏

二叉搜索树

7 篇文章 0 订阅

订阅专栏

Treap平衡树

今天学习了Treap平衡树，记录一下心得。

前导：二叉查找树BST（Binary Search Tree)

概率

二叉查找树(Binary Search Tree)是基于插入思想的一种在线的排序数据结构。它又叫二叉搜索树(Binary Search Tree)、二叉排序树(Binary Sort Tree)，简称 BST。
这种数据结构的基本思想是在二叉树的基础上，规定一定的顺序，使数据可以有序地存储。二叉查找树运用了像二分查找一样的查找方式，并且基于链式结构存储，从而实现了高效的查找效率和完美的插入时间。

定义

二叉查找树(Binary Search Tree)或者是一棵空树，或者是具有下列性质的二叉树：

若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
它的左、右子树也分别为二叉查找树

查找

对于一个已知的二叉查找树，在其中查找特定的值，方法如下。

从根节点开始查找；
如果当前节点的值就是要查找的值，查找成功；
如果要查找的值小于当前节点的值，在当前节点的左子树中查找该值；
如果要查找的值大于当前节点的值，在当前节点的右子树中查找该值；
如果当前节点为空节点，查找失败，二叉查找树中没有要查找的值。

通过返回结点是否为NIL，可以判断查找是否成功。
查找的期望时间复杂度为O(logN)。

插入新结点

在二叉查找树中插入元素，要建立在查找的基础上。基本方法是类似于线性表中的二分查找，不断地在树中缩小范围定位，最终找到一个合适的位置插入。具体方法如下所述。

从根节点开始插入；
如果要插入的值小于等于当前节点的值，在当前节点的左子树中插入；
如果要插入的值大于当前节点的值，在当前节点的右子树中插入；
如果当前节点为空节点，在此建立新的节点，该节点的值为要插入的值，左右子树为空，插入成功。

对于相同的元素，一种方法我们规定把它插入左边或者右边，另一种方法是我们在节点上再加一个域cnt，记录重复节点的个数。
插入的期望时间复杂度为O(logN)。

删除结点

二叉查找树的删除稍有些复杂，要分三种情况分别讨论。基本方法是要先在二叉查找树中找到要删除的结点的位置，然后根据结点分以下情况：
情况一，该节点是叶节点(没有非空子节点的节点)，直接把节点删除即可。
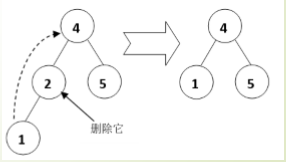
情况二，该节点是链节点(只有一个非空子节点的节点)，为了删除这个节点而不影响它的子树，需要把它的子节点代替它的位置，然后把它删除。如图所示，删除节点2时，需要把它的左子节点代替它的位置。

情况三，该节点有两个非空子节点。由于情况比较复杂，一般的策略是用它右子树的最小值来代替它，然后把它删除。如图所示，删除节点2时，在它的右子树中找到最小的节点3，该节点一定为待删除节点的后继。删除节点3(它可能是叶节点或者链节点)，然后把节点2的值改为3。
也可以使用它的前驱(左子树的最大值)代替它本身。操作方法相同。
为了方便查找后继结点，在每个结点上新增了父指针fa，这样构建的二叉树是双向链表。
插入结点时在维护向下的指针时，也要同步维护向上的指针。

上面其实并不是重点，重点是下面的！！！

二叉查找树的平衡性问题讨论

随机的进行N2(N>=1000)次插入和删除之后，二叉查找树会趋向于向左偏沉。为什么会出现这种情况，原因在于删除时，我们总是选择将待删除节点的后继代替它本身。这样就会造成总是右边的节点数目减少，以至于树向左偏沉。已经被证明，随机插入或删除N2次以后，树的期望深度为Θ(N1/2)。
对待随机的数据二叉查找树已经做得很不错了，但是如果有像这样6,5,4,3,2,1有序的数据插入树中时，会有什么后果出现？如图所示。二叉查找树退化成为了一条链。这个时候，无论是查找、插入还是删除，都退化成了O(N)的时间。
我们需要使二叉查找树变得尽量平衡，才能保证各种操作在 O(logN)的期望时间内完成，于是各种自动平衡二叉查找树 (Self-Balancing Binary Search Tree)因而诞生。

随机二叉查找树Treap

Treap是一种平衡树，在BST的基础上添加一个随机的修正值，Treap节点的修正值也满足最小堆的性质，最小堆性质可以描述为每个子树节点都小于等于其子节点。所以，Treap也被称为堆树或树堆。

Treap满足以下性质：

若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值，而且它的根节点的修正值小于等于左子树根节点的修正值；
若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值，而且它的根节点的修正值小于等于右子树根节点的修正值；
它的左、右子树也分别为Treap。

BST有时会因为数据的特殊性，~~准确说就是一些不良心的出题人，~~而被卡掉，而Treap则是强行将特殊的数据转化为不特殊的数据，从而不被卡掉。当然，随机数据被卡的情况也是有的，只不过几率很小罢了。~~遇到你就可以去买彩票了。~~

为了使Treap中的节点满足BST与小根堆性质，我们需要对这棵树进行旋转操作对其进行调整。

构造

笔者用指针构造的，可以参考。

struct Treap
{
	Treap* ch[2];
	int siz,cnt,val,rnd;
	Treap(int v): val(v){siz=cnt=1;rnd=rand();ch[0]=ch[1]=NULL;}
	int cmp(int x){
		if(x==val) return -1;
		return x<val?0:1;
	}
	void updata(){
		siz=cnt;
		if(ch[0]!=NULL) siz+=ch[0]->siz;
		if(ch[1]!=NULL) siz+=ch[1]->siz;
	}
};
Treap* rt=NULL;

旋转

旋转分为左旋与右旋，对子树来说，具有如下性质：

左旋一个子树，会把它的根节点旋转到根的左子树位置，同时根节点的右子节点成为子树的根；右旋一个子树，会把它的根节点旋转到根的右子树位置，同时根节点的左子节点成为子树的根。
对子树旋转后，子树仍然满足BST性质。

通过旋转的几条重要性质，我们可以通过其来改变树的结构，从而达到我们的目的。

void rotate(Treap* &p,int d)//旋转 ,d==0左旋，d==1右旋 
{
	Treap* k=p->ch[d^1];
	p->ch[d^1]=k->ch[d];
	k->ch[d]=p;
	p->updata();k->updata();
	p=k;
}

插入

在Treap中插入元素，方法与BST插入方法相似，找到合适位置，存储元素，随机生成修订值，但注意过程中注意旋转维护树的结构。

void add(Treap* &p,int x)//插入 
{
	if(p==NULL){p=new Treap(x);return ;}
	if(x==p->val){++p->siz;++p->cnt;return ;}
	int d=p->cmp(x);add(p->ch[d],x);
	if(p->ch[d]->rnd<p->rnd) rotate(p,d^1);
	p->updata();
}

删除

为了维护堆序，所以删除方法与普通BST不大相同，先将要删除的节点旋转至叶子节点，再做删除的操作。

情况一，该节点为叶节点或链节点，则该节点是可以直接删除的节点。若该节点有非空子节点，用非空子节点代替该节点的，否则用空节点代替该节点，然后删除该节点。
情况二，该节点有两个非空子节点。我们的策略是通过旋转，使该节点变为可以直接删除的节点。如果该节点的左子节点的修正值小于右子节点的修正值，右旋该节点，使该节点降为右子树的根节点，然后访问右子树的根节点，继续讨论；反之，左旋该节点，使该节点降为左子树的根节点，然后访问左子树的根节点，继续讨论，知道变成可以直接删除的节点

void del(Treap* &p,int x)//删除 
{
	if(p==NULL) return ;
	if(x==p->val)
	{
		if(p->cnt>1){--p->siz;--p->cnt;return ;}
		if(p->ch[0]==NULL){Treap* k=p;p=p->ch[1];delete(k);}
		else if(p->ch[1]==NULL){Treap* k=p;p=p->ch[0];delete(k);}
		else{
			int dd=p->ch[0]->rnd < p->ch[1]->rnd ? 1:0;
			rotate(p,dd);del(p->ch[dd],x);
		}
	}
	else if(x<p->val) del(p->ch[0],x);
	else del(p->ch[1],x);
	if(p!=NULL) p->updata();
 }

查找元素排名

查找操作与BST相同。

更常用的操作是查找元素的排名。所谓排名是指如果把Treap按照中序遍历，在得到的中序序列中，待查元素应排在什么位置。在维护了siz域的Treap上，查找排名非常好实现。这个实现得非常可靠，即使待查元素不存在，仍然能得到正确的排名。

int rank(Treap* p,int x)//查询排名 
{
	int ss=p->ch[0]==NULL?0:p->ch[0]->siz;
	if(x==p->val) return ss+1;
	else if(x<p->val) return rank(p->ch[0],x);
	else return ss+p->cnt+rank(p->ch[1],x);
}

选取第k小的节点

与查找排名相反，选取第k小的节点是以k为参数，返回对应的节点，可以看作查找排名的反函数。

int kth(Treap* p,int k)//查询第k小 
{
	int ss=p->ch[0]==NULL?0:p->ch[0]->siz;
	if(k<=ss) return kth(p->ch[0],k);
	else if(k<=ss+p->cnt) return p->val;
	else return kth(p->ch[1],k-ss-p->cnt);
}

前驱

前驱即严格小于当前节点的最大节点。

int pre(Treap* p,int x)//前驱 
{
	if(p==NULL) return -INF;
	int d=p->cmp(x);
	if(d==-1||d==0) return pre(p->ch[0],x);
	return max(p->val,pre(p->ch[1],x));
}

后继

后继即严格大于当前节点的最小节点。

int nxt(Treap* p,int x)//后继 
{
	if(p==NULL) return INF;
	int d=p->cmp(x);
	if(d==-1||d==1) return nxt(p->ch[1],x);
	return min(p->val,nxt(p->ch[0],x));
}

例题

可以参见洛谷的【模板】普通平衡树，很模板，就上面的操作。

源码

#include<cstdio>
#include<cmath>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<time.h>
#define MAXN 100005
using namespace std;
typedef long long LL;
const int INF=0x7f7f7f7f;
struct Treap
{
	Treap* ch[2];
	int siz,cnt,val,rnd;
	Treap(int v): val(v){siz=cnt=1;rnd=rand();ch[0]=ch[1]=NULL;}
	int cmp(int x){
		if(x==val) return -1;
		return x<val?0:1;
	}
	void updata(){
		siz=cnt;
		if(ch[0]!=NULL) siz+=ch[0]->siz;
		if(ch[1]!=NULL) siz+=ch[1]->siz;
	}
};
Treap* rt=NULL;
void rotate(Treap* &p,int d)//旋转 ,d==0左旋，d==1右旋 
{
	Treap* k=p->ch[d^1];
	p->ch[d^1]=k->ch[d];
	k->ch[d]=p;
	p->updata();k->updata();
	p=k;
}
void add(Treap* &p,int x)//插入 
{
	if(p==NULL){p=new Treap(x);return ;}
	if(x==p->val){++p->siz;++p->cnt;return ;}
	int d=p->cmp(x);add(p->ch[d],x);
	if(p->ch[d]->rnd<p->rnd) rotate(p,d^1);
	p->updata();
} 
void del(Treap* &p,int x)//删除 
{
	if(p==NULL) return ;
	if(x==p->val)
	{
		if(p->cnt>1){--p->siz;--p->cnt;return ;}
		if(p->ch[0]==NULL){Treap* k=p;p=p->ch[1];delete(k);}
		else if(p->ch[1]==NULL){Treap* k=p;p=p->ch[0];delete(k);}
		else{
			int dd=p->ch[0]->rnd < p->ch[1]->rnd ? 1:0;
			rotate(p,dd);del(p->ch[dd],x);
		}
	}
	else if(x<p->val) del(p->ch[0],x);
	else del(p->ch[1],x);
	if(p!=NULL) p->updata();
 } 
int rank(Treap* p,int x)//查询排名 
{
	int ss=p->ch[0]==NULL?0:p->ch[0]->siz;
	if(x==p->val) return ss+1;
	else if(x<p->val) return rank(p->ch[0],x);
	else return ss+p->cnt+rank(p->ch[1],x);
} 
int kth(Treap* p,int k)//查询第k小 
{
	int ss=p->ch[0]==NULL?0:p->ch[0]->siz;
	if(k<=ss) return kth(p->ch[0],k);
	else if(k<=ss+p->cnt) return p->val;
	else return kth(p->ch[1],k-ss-p->cnt);
}
int pre(Treap* p,int x)//前驱 
{
	if(p==NULL) return -INF;
	int d=p->cmp(x);
	if(d==-1||d==0) return pre(p->ch[0],x);
	return max(p->val,pre(p->ch[1],x));
} 
int nxt(Treap* p,int x)//后继 
{
	if(p==NULL) return INF;
	int d=p->cmp(x);
	if(d==-1||d==1) return nxt(p->ch[1],x);
	return min(p->val,nxt(p->ch[0],x));
}
int n;
signed main()
{
	//srand(time(NULL));
	scanf("%d",&n);
	while(n--)
	{
		int opt,x;
		scanf("%d %d",&opt,&x);
		if(opt==1) add(rt,x);
		if(opt==2) del(rt,x);
		if(opt==3) printf("%d\n",rank(rt,x));
		if(opt==4) printf("%d\n",kth(rt,x));
		if(opt==5) printf("%d\n",pre(rt,x));
		if(opt==6) printf("%d\n",nxt(rt,x));
	}
	return 0;
}

谢谢！！！

StaroForgin

关注

2
点赞
踩
2

收藏

觉得还不错? 一键收藏
0
评论
Treap平衡树学习

Treap平衡树今天学习了Treap平衡树，记录一下心得。前导：二叉查找树BST（Binary Search Tree)概率二叉查找树(Binary Search Tree)是基于插入思想的一种在线的排序数据结构。它又叫二叉搜索树(Binary Search Tree)、二叉排序树(Binary Sort Tree)，简称 BST。这种数据结构的基本思想是在二叉树的基础上，...
复制链接

扫一扫