2023.2.25 J 课时3 小结

引言——

说来惭愧，到要上课了才找到时间来写小结

正文部分——

我们之前已经讲过了线段树的一些基本的操作，包括单点修改，单点查询，区间修改（懒标记）和区间查询。

然后还留了个很恐怖的东西——可持久化线段树。

可持久化线段树，网络上更流行叫“主席树”。所谓的可持久化，就是说我在对任意一个节点改了N次之后，我仍然能找到第i次修改时这个树的状态，换言之，就是支持历史修改与查询。

咱们先放着这个东西怎么实现，先看一个更现实的问题——这种线段树有什么用？

1、可持久化线段树的用处

先说一个你们可能看起来觉得弱智的题目

我有一个序列A，现在给出了序列A中的每个元素，接下来我想多次提问：L~R这一段的第k小的数是哪一个？（L，R，k在每次询问时给出）

a.思路分析

这好像不是线段树的活。

线段树针对的是区间的查询修改，也可以是单点，一般来说是动态的（也就是有修改，替换的），而这题则是静态的（A序列从头到尾都没变）

那么现在再想，真的要实现，怎么做呢？

排序？？？

讲个不幸的消息：这题的A的长度是10^5级别的，询问个数也是10^5的级别的。因为每次要求的都是第k小，所以每次都得对L，R排序，而排序的复杂度是nlogn，也就意味着如果题目的测评数据每次的L，R都给到10^5（你不知道这个范围重不重啊），你就要做这么一个时间范围：

10^10log10^5

也没什么对吧，不是就妥妥TLE嘛（逃）

所以排序的路，行不通。

如何加速？？？

能不能快速查找到那个第k小的元素呢？

如果每次真的存储元素，然后通过比较大小来确定大于我的和小于我的各有多少，我们实际上还是回到了排序的老路上。现在我们可以用另一种思路。

我们可以用一颗树来存储出现在这个区间内的元素个数，这样，在元素有序的情况下，我们就可以用二分查找树的思想，左右子树分别判断范围，然后确定第k小在哪边了。

b.方式假设

我们肯定不能把每一段L，R都整成一颗树啊。

那有没有什么方式，能让我们省空间呢？

第一次省空间——前缀和思想

我们可以每次都对1~i这一段进行建树，举个例子：

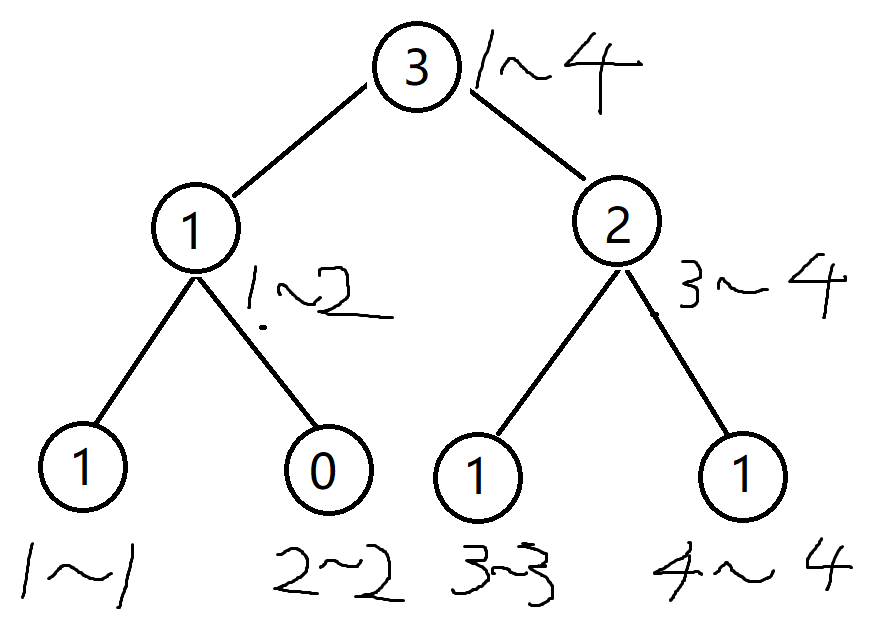
这是对[1,4]这段长度所对应的线段树。现在，我们已经能够解决L为1的情况的所有的第k小了——查找即可。现在，如果L不为1，我们来看看到底怎么做。

现在我要求的区间是3~4中的第k大。

这里给出了1~2和1~4这两颗线段树，我们会发现，除了新增的一个根节点，1~4这棵线段树出去1~2的部分就是我们要找的3~4的范围。而这，恰好就能运用前缀和。即：第R棵树-第L-1棵树，就会是我们要的L~R的线段树。

如果你有一定的前缀和基础，那么相信理解这部分内容没有难度。

那么L~R的线段树有了，我们不就可以按照之前说的，直接二分搜索了吗？

2、可持久化线段树的实现

肯定会有人觉得我前面讲的很少。的确，因为我们前面只是提纲挈领的拎个思路，稍稍讲个实现的假设，那么接下来，我们来讲实现的步骤。不过在这之前，我们还有个大问题，那就是：

如果是第i棵线段树，那么大概有2i-1个节点。也就意味着大致要4i-4的内存，而i有事不断增大的，一直到N，也就意味着当N在10^6的级别的时候，会有：

4*1-4+4*2-4+……+4*10^6-4=499995500000这么点大的内存

也没什么，不就妥妥MLE嘛（逃）

那么怎么办呢？

我们先假设有一棵空树，那么每读进一个ai，就是等于新增加一个节点，而每新增加一个节点，实际上需要更改的只有logn个节点。

示意图如下：

我们会发现，只有这个叶子节点所在的这条链惨遭修改。那么，内存问题就解决啦。

反正你只有这条链不一样：我就只存每一次不一样的这条链不就得了？？

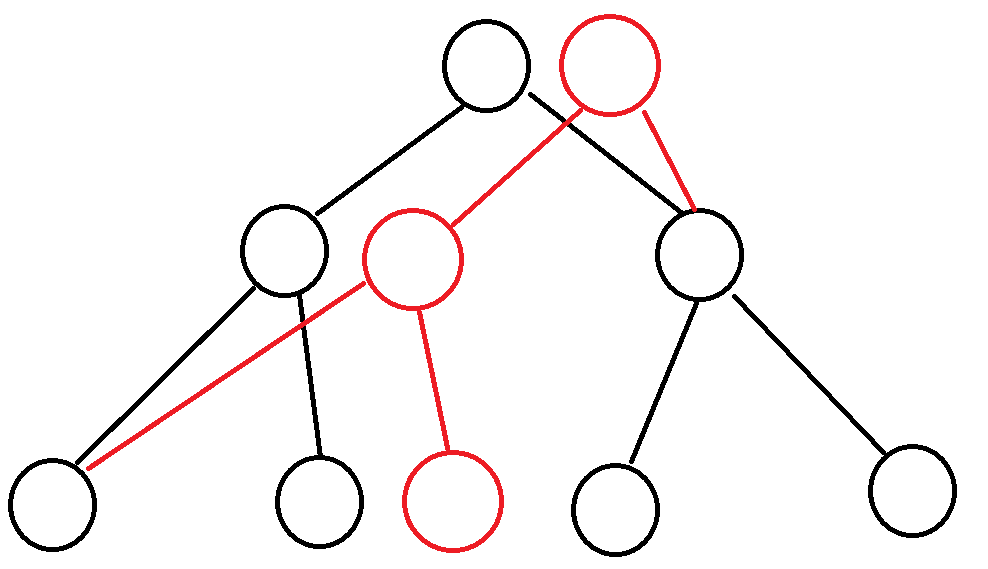
这里，红色的节点是我们存储的被修改的那一条链，黑色的则是原状态，这样，虽然内存上不连续，但是逻辑连续。而且内存也省了下来。

那么内存问题解决了，接下来我们看看到底怎么写代码。

一个节点的信息存储

struct node{
    ll L;//左子树 
    ll R;//右子树 
    ll sum;//节点i权值 
}tree[N<<5];//注意,n<<4是不够的,n<<5勉强 

1、建树操作

这里的建树操作和我们之前的建树基本上一样，但是实际上这棵空树是不必要建的。因为每读入一个节点，就一这个节点新建一条链就足够了。这样只是为了让整个代码逻辑更加清晰一些。

ll build(ll pl,ll pr){//建一颗空树，除了耗时间没有任何用 
    ll rt=++cnt;//节点编号++ 
    tree[rt].sum=0;//权值初始化为0 
    ll mid=(pl+pr)>>1;
    if(pl<pr){//等于时结束，就是不写人话 
        tree[rt].L=build(pl,mid);//左右分别递归 
        tree[rt].R=build(mid+1,pr);
    }
    return rt;
} 

注意，这里的pl<pr实际上就是之前的pl==pr break；这种操作，两者相等就停止循环。

2、修改操作（新建一条链）

这里我们的修改实际上就是新建一条链，因为我们的背景题目它是静态的，也就意味着是用不到区间/单点修改的。

ll update(ll pre,ll pl,ll pr,ll x){//新建一颗logn的树，就是记录一条不同的路径 
    ll rt=++cnt;
    tree[rt].L=tree[pre].L;//先把前一颗树的左右节点赋予到这棵树 
    tree[rt].R=tree[pre].R;
    tree[rt].sum=tree[pre].sum+1;//多一个节点 
    ll mid=(pl+pr)>>1;
    if(pl<pr){
        if(x<=mid)//x的位置在左子树 
            tree[rt].L=update(tree[pre].L,pl,mid,x);
        else//右子树 
            tree[rt].R=update(tree[pre].R,mid+1,pr,x);
    }
    return rt;
}

这可能是所有的操作中最难的一个。首先，如果要想新建一条logn的链，那么就要将前一个状态(pre)传过来，并且要判断现在建树的这个节点(x)的位置，并不断的递归分化给rt的左右子树。

3、查询操作

查询的时候要通过当前的L,R区间的节点数来判断往那颗子树递归。

ll query(ll L,ll R,ll pl,ll pr,ll k){
    if(pl==pr)
        return pl;
    ll _dec=tree[tree[R].L].sum-tree[tree[L].L].sum;//这一棵线段树减去前一棵，就是需要的区间 
    ll mid=(pl+pr)>>1;
    if(_dec>=k)//k在左子树 
        return query(tree[L].L,tree[R].L,pl,mid,k);
    else//右子树 
        return query(tree[L].R,tree[R].R,mid+1,pr,k-_dec);        
}

这里查询的时候注意，如果是往左子树查询，那么就意味着仍然是找第k大的（右子树全部比我大），但是如果是往右子树查询，就得减去左子树比我小的了（右子树的第1大，是整棵树的第左子树节点个数+右子树节点大）

3、实战演练

上述代码放给了大家之后，我们只是完成了线段树的内部实现，但是怎么使用，我们还得看题。

接下来，就请大家看今天引入时问题的原题：P3834 【模板】可持久化线段树 2

线段树部分我就不多说了，现在我们看主函数的实现。

首先，我们只要不一样的元素——只有他们对我们的排名有用。

其次，我们进行离散化——保证所有元素有序，并且可以找到原位置输出

最后，我们进行调用——AC！！！

你以为我要放全部代码？想得美！

    sort(b+1,b+1+n);
    ll size=unique(b+1,b+1+n)-b-1;//unique去重，只要不同的个数 
    root[0]=build(1,size);//建树，实际上就是耗时间 
    for(int i=1;i<=n;++i){
        ll x=lower_bound(b+1,b+1+size,a[i])-b;//寻找离散化后的位置 
        root[i]=update(root[i-1],1,size,x);//建树 
    }

这里的b数组时拷贝的原序列，root[i]则是每棵树（不是有n棵吗）的根节点，你可以看到对新建链的调用。而这里的unique是STL自带去重函数，lower_bound则是为了快速查找离散化之后元素的位置。

接下来就没什么好说的了，我相信这道题应该可以轻松做出来了。

完整代码：

//洛谷P3834 可持久化线段树（主席树）模板
#include<bits/stdc++.h>
#define ll long long
#define N 200010
using namespace std;
ll cnt=0;//可使用的新节点 
ll a[N],b[N],root[N];//a为原数组，b为排序后的数组，root[i]表示新建的线段树以i为根节点 
struct node{
    ll L;//左子树 
    ll R;//右子树 
    ll sum;//节点i权值 
}tree[N<<5];//注意,n<<4是不够的,n<<5勉强 
ll build(ll pl,ll pr){//建一颗空树，除了耗时间没有任何用 
    ll rt=++cnt;//节点编号++ 
    tree[rt].sum=0;//权值初始化为0 
    ll mid=(pl+pr)>>1;
    if(pl<pr){//等于时结束，就是不写人话 
        tree[rt].L=build(pl,mid);//左右分别递归 
        tree[rt].R=build(mid+1,pr);
    }
    return rt;
} 
ll update(ll pre,ll pl,ll pr,ll x){//新建一颗logn的树，就是记录一条不同的路径 
    ll rt=++cnt;
    tree[rt].L=tree[pre].L;//先把前一颗树的左右节点赋予到这棵树 
    tree[rt].R=tree[pre].R;
    tree[rt].sum=tree[pre].sum+1;//多一个节点 
    ll mid=(pl+pr)>>1;
    if(pl<pr){
        if(x<=mid)//x的位置在左子树 
            tree[rt].L=update(tree[pre].L,pl,mid,x);
        else//右子树 
            tree[rt].R=update(tree[pre].R,mid+1,pr,x);
    }
    return rt;
}
ll query(ll L,ll R,ll pl,ll pr,ll k){
    if(pl==pr)
        return pl;
    ll _dec=tree[tree[R].L].sum-tree[tree[L].L].sum;//这一棵线段树减去前一棵，就是需要的区间 
    ll mid=(pl+pr)>>1;
    if(_dec>=k)//k在左子树 
        return query(tree[L].L,tree[R].L,pl,mid,k);
    else//右子树 
        return query(tree[L].R,tree[R].R,mid+1,pr,k-_dec);        
}
int main(){
//  freopen(".in","r",stdin);
//  freopen(".out","w",stdout);
    ll n,m;
    scanf("%lld%lld",&n,&m);
    for(int i=1;i<=n;++i){
        scanf("%lld",&a[i]);
        b[i]=a[i];
    }
    sort(b+1,b+1+n);
    ll size=unique(b+1,b+1+n)-b-1;//unique去重，只要不同的个数 
    root[0]=build(1,size);//建树，实际上就是耗时间 
    for(int i=1;i<=n;++i){
        ll x=lower_bound(b+1,b+1+size,a[i])-b;//寻找离散化后的位置 
        root[i]=update(root[i-1],1,size,x);//建树 
    }
    while(m--){
        ll x,y,k;
        scanf("%lld%lld%lld",&x,&y,&k);
        ll t=query(root[x-1],root[y],1,size,k);//寻找区间[x,y]的线段树 
        printf("%lld\n",b[t]);
    }
    return 0;
}

结语——

终于搞完了！但是主席树并不是最难的算法，接下来我们会经历一个更加恐怖的东西——扫描线。