Preface:
本文主要介绍Matlab R2022b版本中偏微分方程工具箱的基础用法,是个人学习时写的入门笔记(学的非常浅),内容主要包括以下几方面:
1.Matlab中偏微分方程工具箱简介。
2.双曲线型PDE,生成动画。
3.椭圆形非线性PDE,参数为函数,应用非线性解法。
4.椭圆形线性PDE,用实际物理问题模板,解热传导方程。
5.椭圆形线性PDE,正常解法,画图。
6.抛物线型PDE,正常解,热传导问题,生成动画。
一.工具箱介绍
1.简介
MATLAB中的PDE工具箱具有强大功能,用于解决偏微分方程和边界值问题。它是MATLAB的一个附加组件,为工程师、科学家和数学家提供了一个方便的方式来建模、分析和解决各种PDE问题。下面是PDE工具箱的一些主要功能和特点:
-
图形用户界面(GUI): PDE工具箱提供了一个直观的GUI,称为PDE工具,用于建立和编辑PDE模型。这个GUI使用户能够轻松地定义几何形状、设置边界条件和初始化条件,以及选择求解器。
-
支持多种PDE类型: PDE工具箱支持各种PDE类型,包括椭圆型、抛物型和双曲型PDE。用户可以选择适合其特定问题的PDE类型,并进行相应的分析和求解。
-
自定义几何形状: 用户可以使用PDE工具箱创建自定义的几何形状,以反映其实际问题。这使得模拟各种真实世界应用变得更加容易。
-
边界条件设置: 工具箱允许用户指定各种边界条件,包括固定值、导数值和自定义函数,以模拟问题的真实边界条件。
-
初始条件设置: 用户可以设置初始条件,以定义问题的初始状态。这对于时间依赖的问题非常重要。
-
求解器选择: PDE工具箱提供了多种求解器选项,用户可以选择合适的求解器来解决其问题。这些求解器包括有限元法、有限差分法等。
-
结果可视化: 工具箱提供了丰富的结果可视化功能,用户可以轻松地查看模拟结果,包括温度分布、应力分布等等。
-
脚本支持: 对于高级用户,PDE工具箱也支持MATLAB脚本,使他们能够更精细地控制问题的建模和求解过程。
-
应用领域广泛: PDE工具箱可用于多个领域,包括物理学、工程学、生物医学等等,用于解决各种PDE问题。
2.基础操作
- 区域绘制:打开Options-grid网格,设置Axes limits边界,Axes equal边界等宽(不设鼠标右键画圆可能不标准),Draw mode,绘制完,进行交并补运算,交并用括号分开,Boundary mode,Remove all subdomain Borders去除多余部分。

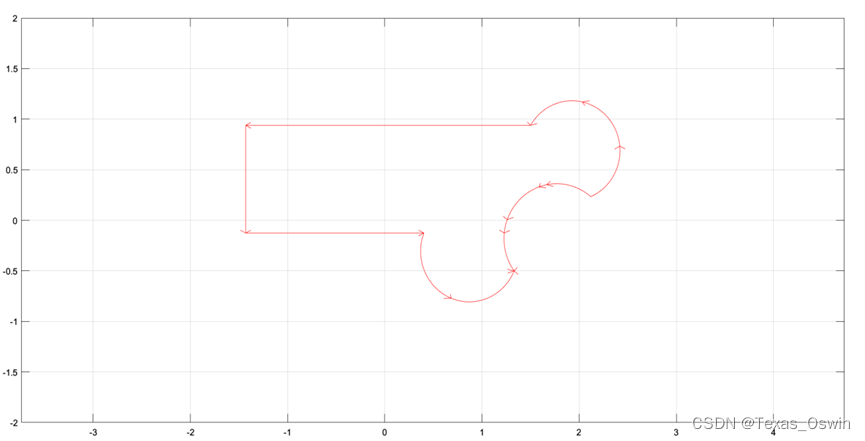
- 点击
 生成网格,网格越密越精准:
生成网格,网格越密越精准:

- 配置边界条件:
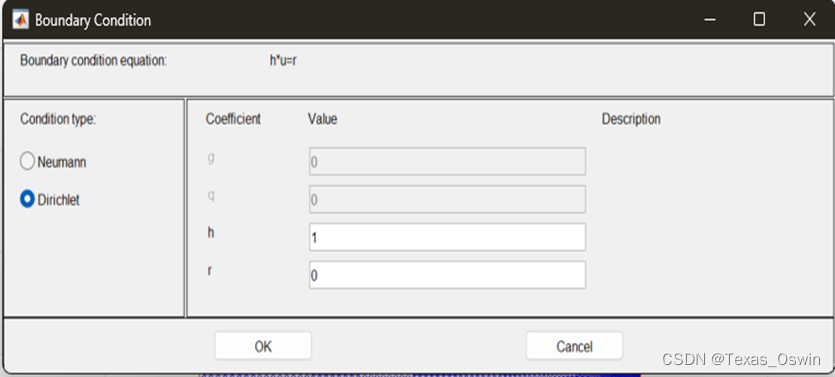
说明:Dirichlet边界一般h=1,r可为x、u的函数或者偏导。Hyperbolic是双曲型,parabolic是抛物线型。div是一阶偏导。PDE默认时间向量是t=0:10,后面生成pde输出随时间变化的gif时用到。
- UI工具:工具箱上方的
 为绘制多边形,右键封口。
为绘制多边形,右键封口。 为边界模式。
为边界模式。 为集合运算 。
为集合运算 。
二.PDE TOOL解二阶PDE示例
1.双曲型PDE,u对t二阶导,参数全为实数:

- 边界条件:边界上所有u为5,求解区域同上面的基础操作中绘制的区域。

- 对比上面的双曲型标准PDE得出4个参数,点
 配置偏微分方程:
配置偏微分方程:

- 修改边界条件:

- 边界上u都是5,在Dirichlet里令r为5,点
 得出t=10时刻的解:
得出t=10时刻的解:
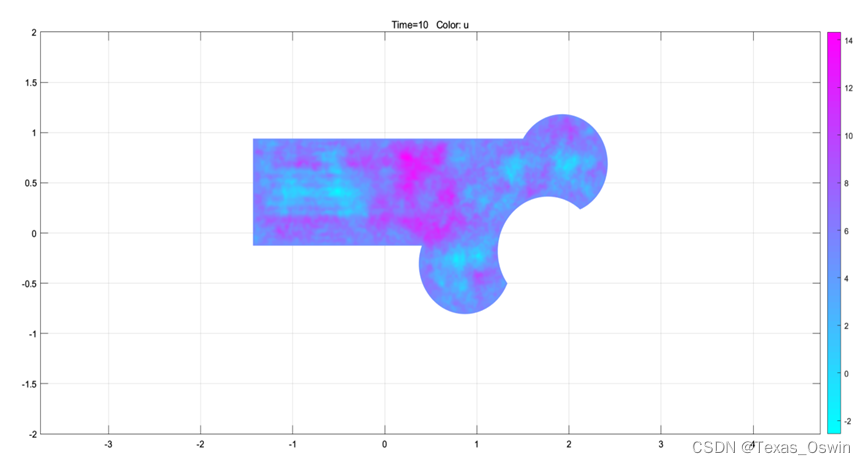
- 点
 设置出图选项:
设置出图选项:

Contour:等值线
Arrows:引力线
Height(3D):绘制3D图
Animation:绘制动画,options里设置重复和帧率
Colormap:设置解的图形颜色
Time for plot:出图时刻
- 等值线:t=10
-
引力线:t=10

- 3D:t=10,下图分别为有颜色与无颜色:
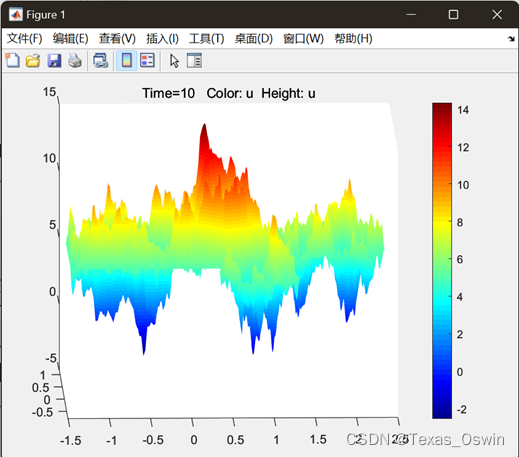

- 改变t=5,Time for plot选5

- 因为方程是u对x,y,t的函数,方程的解应为动画。
-
点Solve里的parameters设置时间向量:0:0.1:4。回Plot Selection设置帧率和重复次数。


- 横纵坐标代表x,y,颜色深浅代表u,u相当于z轴垂直于平面,在不同位置不同时间u不同。
2.非线性椭圆形PDE,u对t不求导,参数为函数

- 边界为0,区域如和刚才一样。
- 首先配置PDE,对比标准型得到3个参数:
c=1./sqrt(1+ux.^2+uy.^2),a=x.^2+y.^2,
f=exp(-x.^2-y.^2)
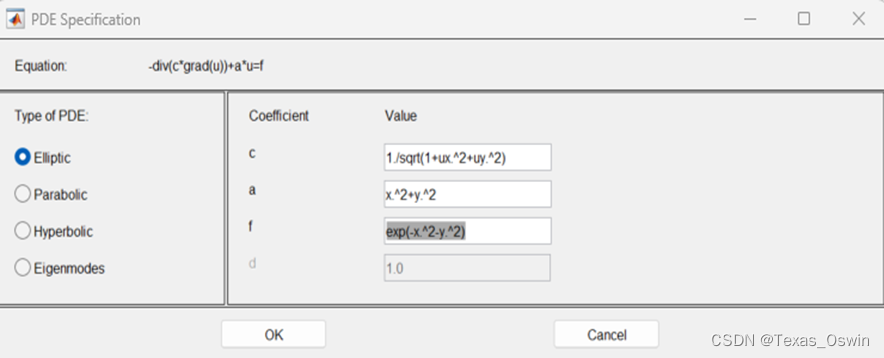
- 配置边界条件:Specify Boundary Conditions

- 观察方程:u只与x,y有关与t无关不用考虑时间变量,边界条件是边界为0所以用Dirichlet,本题椭圆形PDE为非线性。因为是非线性椭圆形PDE所以用非线性求解方法。在Solve Parameters里设置:(只适用椭圆形)

- 求解结果:

- 等值线:

- 引力线:

- 3D:

3.线性椭圆型PDE:热传导问题,u对t不求导,区域如前。

- 热传导系数:λ=30W/(m*K)

- 空气热对流系数:h=100W/K*m2

- 外界温度:Text=425K

- 法相热流密度:q0=1000W/s*m

- 内部热源:Q=0
正常椭圆型PDE:

因为本体为实际问题所以解法不同,前两道题都是普通PDE问题。![]()
首先在PDE工具箱上方选择问题类别:
配置本题PDE:

配置边界条件:本题为诺伊曼边界条件,将参数带入边界条件: ,简化:
,简化: 对比诺尼曼边界条件标准型得:q=0,g=33.33
对比诺尼曼边界条件标准型得:q=0,g=33.33

求解结果:


4.线性椭圆形Poisson PDE 边值问题

精确解: 用PDE tool仿真。
用PDE tool仿真。
- 绘制求解区域:先画一个圆然后双击修改参数


- 配置边界条件:因为是边值问题所以用Dirichlet
-
先点Boundary里Boundary Mode再点Specify配置
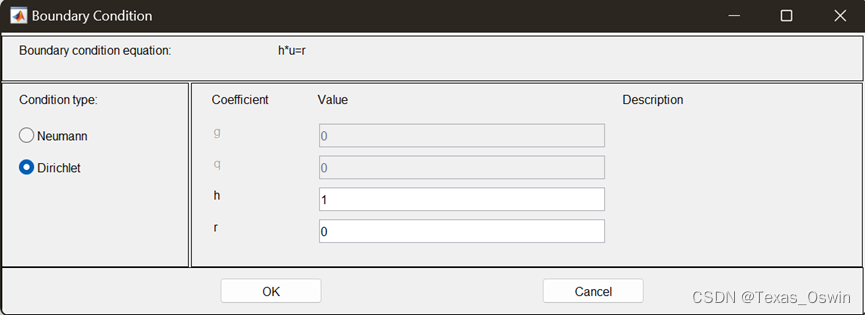
配置PDE:div=∆![]() ,对比参数得到c,a,f
,对比参数得到c,a,f
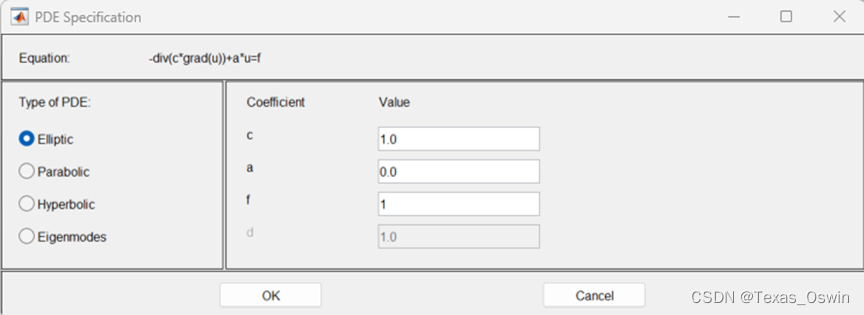
- 网格化后求解:
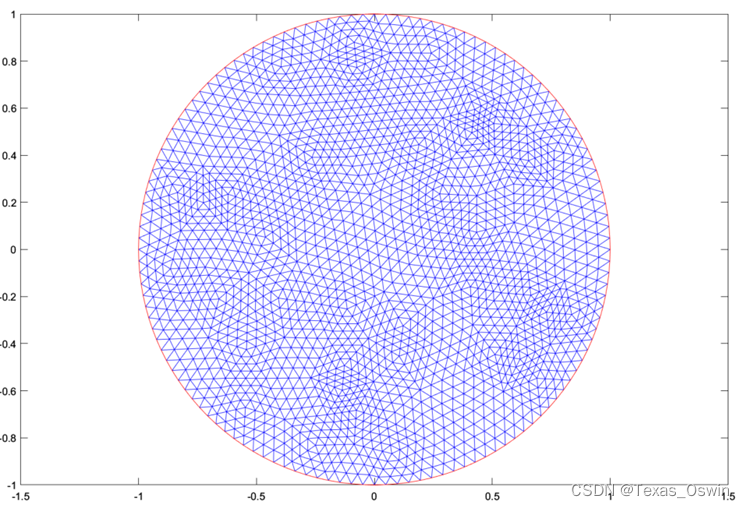

- 等值线,引力线:

- 3D:

5. 抛物线型热传导方程:u对t求一阶导


- 绘制正方形求解区域:先画一个矩形双击修改

- Left是底边左端横坐标,Bottom是底边纵坐标,Width和Height对应宽高。设置坐标轴等宽,不然PDE tool显示与显示器分辨率有关看上去不像正方形。

- 配置PDE:对比得参数。

- 配置边界条件:边界上所有点值为φ(x,y)
 ,abs为绝对值
,abs为绝对值

- 配置时间向量、初值IC:Solve里parameters后两项为公差和绝对公差。

- 网格化、求解PDE:
等值线:
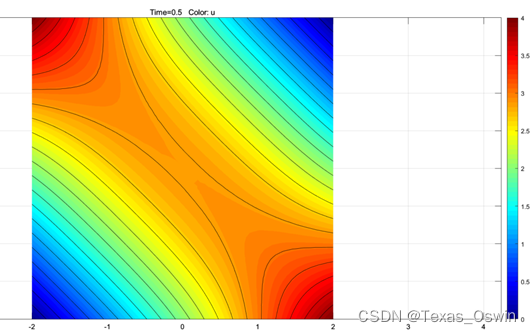
配置输出:

配置动图格式:fps越高动画越快,10即可。

Plot:
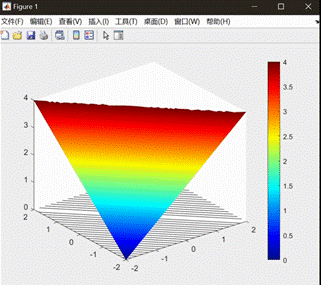
结论:初始条件不光滑但方程解可能是光滑的。
实际物理问题MATLAB有现成模板可以选择:
Generic scalar:泛型标量 generic system:通用系统
Structural mesh,Plane stress:结构力学、平面应力
Structural mesh,Plane strain:平面应变(张力)
Electron statics:静电学 magnetostatics:静磁学
AC Power Electromagnetics:交流功率电磁学
Conductive Media DC:直流导电介质 Diffusion:扩散










 本文详细介绍了MatlabR2022b版本中偏微分方程工具箱的基础用法,涵盖双曲型、椭圆形和抛物线型PDE,涉及动画生成、边界条件设定、求解方法和实际物理问题应用等内容。
本文详细介绍了MatlabR2022b版本中偏微分方程工具箱的基础用法,涵盖双曲型、椭圆形和抛物线型PDE,涉及动画生成、边界条件设定、求解方法和实际物理问题应用等内容。
















 896
896

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








