动态规划入门==》转换为DAG问题——最短路径|矩阵嵌套|硬币问题

动态规划刚刚开始学习，到现在做过几道题，借鉴了各位大神的书籍文章后，对其有了新的看法。

现在我总结目前我遇到题目动态规划思想的共性——很多动态规划都可以转化为带权DAG问题，以下是几道题题，我从中总结了他们的DAG特性

一、DAG最短路径

在我们聊DAG时先来介绍一个最直接的DAG问题

问题描述：

给一个带权有向无环图G=（V，E），找出这个图里S==>E的最短路径。

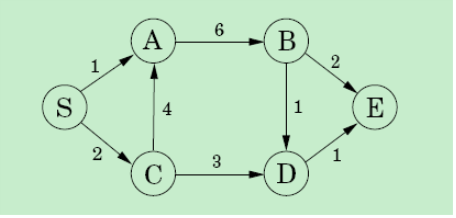
这个问题用贪心算法的话不能得到全局最优解

我们用动态规划思想，考虑DAG问题

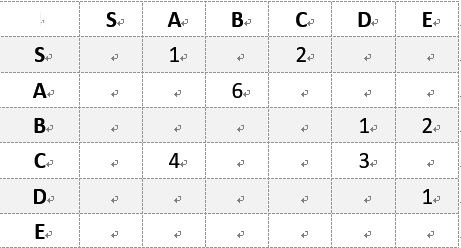
1.首先在数据结构上我们可以用二维数组的形式表示这个DAG，为了方便，用Q(S,N)表示S到N的最短路径

2.问题小化，直接求Q(S,E)求不出来，因为S到E没有联通，但是Q（D,E）=1,Q(B,E)=2易求，那我们只要知道Q(S,D)和Q(S,B)然后Q（S,E）=min{ Q（S,D）+1,Q（S,B）+2},Q（S，D)和Q（S，B）我们同理也可以通过求Q(S,A)Q(S,C)得出。以此类推。

3.数据结构表示，我们用dp['N'-'A']  来存储Q(S,N)

4.伪代码实现

4.1正常预处理，把点都用拓扑排序排好,dp全初始化为0,这里设R(T,M)为T到N的路径消耗

solve（）{

拓扑排序（全部点），dp全初始化为0

for(M ： 全部点)

    for（舍T= A~M即M之前的点）{

         if（T可以连向M）dp[M-‘A’]=min(dp[T]+R(T,M),dp[M-'A']);

    }

    return dp['E'-'A']

}

4.2递归处理方法

Q（T，M）{

    if(R(T,M)可以连接z)

        returnR(T,M)

    不能连接则 查表找出指入M的所有点集合Ms

        return Min(Q(T,Ms)+R(Ms,M))//返回所有点集合中（最短路径+当前消耗）最短的

}

二、信封嵌套问题（嵌套矩形问题）

当然别的某些动态规划解法问题也可以想象成DAG

这里跟我之前一篇关于动态规划的博客的问题是一样的，但是思想的角度不一样。

问题描述：

有n个矩形，每个矩形可以用两个整数a、b描述，表示它的长和宽。 矩形X(a,b)可以嵌套在矩形Y(c, d)中，当且仅当a＜